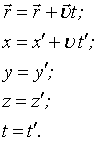6. Обертовий рух. Основний закон динаміки обертового руху. Теорема Штейнера.

Обертальний рух - вид механічного руху. При обертальному русі абсолютно твердого тіла його точки описують кола, розташовані в паралельних площинах. Центри всіх кіл лежать при цьому на одній прямій, перпендикулярній до площин кіл і званої віссю обертання. Вісь обертання може розташовуватися усередині тіла і за його межами. Вісь обертання в даній системі відліку може бути як рухомий, так і нерухомою. Наприклад, у системі відліку, пов'язаної з Землею, вісь обертання ротора генератора на електростанції нерухома.

Характеристики обертання тіла

При рівномірному обертанні (T оборотів в секунду),

•  Частота обертання - число обертів тіла в одиницю часу.

 ,

•  Період обертання -час одного повного обороту. Період обертання T і його частота ν зв'язані співвідношенням T = 1 / ν .

•  Лінійна швидкість точки, що знаходиться на відстані R від осі обертання

 ,

•  Кутова швидкість обертання тіла

 .

•  Момент інерції механічної системи відносно нерухомої осі a ("осьовий момент інерції") - фізична величина J _a, яка дорівнює сумі творів мас всіх n матеріальних точок системи на квадрати їх відстаней до осі:

 ,

де: m _i - маса i-й точки, r _i - відстань від i-й точки до осі.

Осьовий момент інерції тіла J _a є мірою інертності тіла в обертальному русі навколо осі a подібно до того, якмаса тіла є мірою його інертності в поступальному русі.

•  Кінетична енергія обертального руху

де I _z - момент інерції тіла відносно осі обертання. ω - кутова швидкість

Основне рівняння динаміки обертального руху твердого тіла.

При повороті тіла під дією сили   на нескінченно малий кут   точка прикладання сили проходить шлях   і робота дорівнює:

Оскільки

Тоді  , або 

Звідси рівняння динаміки обертального руху твердого тіла:

Якщо вісь обертання співпадає з головною віссю інерції, що проходить через центр мас, то має місце векторна рівність:

де J – головний момент інерції тіла.

Якщо відомий момент інерції тіла відносно осі, яка проходить через його центр мас  , то момент інерції відносно осі, паралельної до вказаної – J_Z, визначається за теоремою Штайнера:

М омент інерції тіла J_z відносно довільної осі дорівнює сумі моменту інерції J_С відносно осі, паралельної даній, що проходить через центр мас тіла і добутку маси тіла m на квадрат відстані між осями d .

.

7.Механічний принцип відносності і перетворення Галілея.

Якщо в системі відліку на матеріальну точку не діють інші тіла і точка рухається відносно даної системи відліку прямолінійно і рівномірно (тобто за інерцією), то таку систему називають інерціальною.  

Дослідження показали, що закони Ньютона виконуються лише в інерціальних системах відліку. Наближено, в межах точності експерименту, інерціальними можна вважати системи відліку зв’язані з Землею, Сонцем чи зорями.

На основі експериментальних даних Галілей встановив, що всі механічні явища в різних інерціальних системах відліку протікають однаково, тобто ніякими механічними дослідами, що проводяться в даній інерціальній системі, неможливо встановити: знаходиться дана система в спокої чи рухається прямолінійно і рівномірно відносно іншої інерціальної системи. Це положення носить назву механічного принципу відносності Галілея.   

Система, що рухається з прискоренням відносно інерціальної системи є неінерціальною.

Нехай інерціальна система відліку   рухається рівномірно і прямолінійно з швидкістю    відносно іншої інерціальної системи  . Рух відбувається так, що   і в початковий момент часу   початки відліку обох систем співпадали.

        Нехай матеріальна точка   знаходиться в спокої в системі  . Відносно  точка   рухається.

 

Рис. 1

        Час в обох системах протікає однаково. Тому положення точки   в момент часу   характеризується як координатами так і радіус-вектором в обох системах:

Значення цих величин в рухомій системі координат   називається прямими перетворенями Галілея:                  

        Рівняння руху точки   в нерухомій системі відліку  описується оберненими перетвореннями Галілея