
- •4.2. Основні елементи кінематики рівномірного обертального руху
- •5. Закон Гука. Діаграма напружень.
- •6. Обертовий рух. Основний закон динаміки обертового руху. Теорема Штейнера.
- •7.Механічний принцип відносності і перетворення Галілея.
- •8. Елементи ств Енштейна. Перетворення Лоренца і наслідки що з нього випливають.
- •5.Фаза коливань.
- •Перетворення енергії при гармонічних коливаннях
- •18. Основне рівняння мкт ідеального газу
- •17/////4.6. Внутрішня енергія і теплоємність ідеального газу
- •Розподіл частинок у потенціальному силовому полі
- •Перше начало термодинаміки
- •21. Оборотні процеси. Цикли. Теплові двигуни і холодильні машини. Друге начало термодинаміки.
- •33. Робота і потужність у колі постійного струму. Закон Джоуля-Ленца
- •34. Розгалужені кола. Правила Кірхгофа.
- •35. Електричний струм в металах, газах та рідинах.
- •36. Магнітне поле та його характеристики.
- •41 Самоіндукція і взаємоіндукція. Індуктивність.
- •42 Енергія магнітного поля.
- •§ 2. Інтерференція світла в тонких плівках
- •49 Дифракція світла
- •Дифракція на щілині[
- •55. Закони випромінювання абсолютно чорного тіла Закон випромінювання Планка
- •Три закони фотоефекту:
- •58. Ефект Комптона
- •61.Співвідношення невизначеностей Гейзенберга
- •62.Хвильова функція і її статистичний зміст
- •63.Рівняння Шредінгера
- •64. Постулати Бору
- •69. Реакції поділу та синтезу ядер.
- •70. Природна радіоактивність ядер. Закон радіоактивного розпаду.
63.Рівняння Шредінгера
Статистичне
трактування хвиль де Бройля і співвідношення
невизначеностей Гейзенберга привели
до висновку, що рівнянням руху в квантовій
механіці, яке описує рух мікрочастинок
в різних силових полях, повинно бути
рівняння, з якого би виходили хвильові
властивості частинок, які спостерігаються
під час досліду. Основне рівняння повинно
бути рівнянням відносно хвильової
функції
![]() ,
оскільки саме вона, або, точніше, величина
,
визначає ймовірність перебування
частинок у момент часу t в об’ємі
dV. Оскільки шукане рівняння повинно
враховувати хвильові властивості
частинок, то воно повинно бути хвильовим
рівнянням.
,
оскільки саме вона, або, точніше, величина
,
визначає ймовірність перебування
частинок у момент часу t в об’ємі
dV. Оскільки шукане рівняння повинно
враховувати хвильові властивості
частинок, то воно повинно бути хвильовим
рівнянням.
Основне рівняння нерелятивістської квантової механіки сформульовано в 1926 р. Е. Шредінгером. Рівняння Шредінгера, як і всі основні рівняння фізики, не виводиться, а постулюється. Правильність цього рівняння підтверджується узгодженням з експериментами, що, у свою чергу, надає йому характер закону природи.
Рівняння Шредінгера має такий вигляд:
![]() ,
,
де
![]() ,m
– маса частинки,
,m
– маса частинки,
![]() –
оператор Лапласа, (
–
оператор Лапласа, (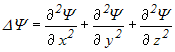 ),
),
![]() –
потенціальна енергія частинки в силовому
полі, в якому рухається частинка,
–
потенціальна енергія частинки в силовому
полі, в якому рухається частинка,
![]() –
уявна одиниця.
–
уявна одиниця.
З погляду математики рівняння Шредінгера є лінійним диференціальним рівнянням з частинними похідними. З теорії диференціальних рівнянь відомо, що кожне лінійне рівняння з частинними похідними має багато розв’язків, причому таких, що лінійна комбінація будь-якої сукупності розв’язків рівняння також буде розв’язком рівняння.
Це
рівняння справедливе для довільної
частинки, яка рухається з малою швидкістю
(![]() ).
).
Записане вище рівняння Шредінгера називають рівнянням Шредінгера, що залежить від часу, бо воно містить похідну від функції по часу.
Проте для значної кількості фізичних явищ, які відбуваються в мікросвіті, наприклад, для опису поведінки електрона в атомі у ряді випадків важливо вміти знаходити стаціонарні розв’язки рівняння Шредінгера, які не містять часу.
Щоб
розв’язати цю задачу, треба знайти так
зване стаціонарне рівняння Шредінгера,
в якому виключено залежність
від
часу. Воно має сенс для тих задач, в яких
потенціальна енергія U не залежить
від часу:
![]() .
Шукатимемо розв’язок рівняння Шредінгера
у вигляді добутку:
.
Шукатимемо розв’язок рівняння Шредінгера
у вигляді добутку:
![]() ,
,
де
![]() є
функцією лише координат, а
є
функцією лише координат, а
![]() –
повна енергія частинки.
–
повна енергія частинки.
Підставимо вираз для у рівняння Шредінгера

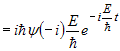 .
.
Скоротивши
на множник
![]() ,
отримаємо
,
отримаємо
![]() .
.
Це стаціонарне рівняння Шредінгера.
Наведене
рівняння – найважливіше співвідношення
нерелятивістської квантової механіки.
Функції
![]() ,
які задовольняють рівняння Шредінгера
при певному Е, називають власними
функціями. В рівнянні Шредінгера
як параметр входить повна енергія
частинки. В теорії диференціальних
рівнянь доводиться, що подібні рівняння
мають розв’язок не при довільних
значеннях параметра, а лише при певних
значеннях Е. Ці значення енергії
називають власними.
,
які задовольняють рівняння Шредінгера
при певному Е, називають власними
функціями. В рівнянні Шредінгера
як параметр входить повна енергія
частинки. В теорії диференціальних
рівнянь доводиться, що подібні рівняння
мають розв’язок не при довільних
значеннях параметра, а лише при певних
значеннях Е. Ці значення енергії
називають власними.
Власні значення Е можуть утворювати як неперервний, так і дискретний ряд. У першому випадку говорять про неперервний, або суцільний спектр, у другому – про дискретний спектр.
64. Постулати Бору
До 1913 р. були три експериментальні факти, які не знаходили пояснення в рамках класичної фізики:
Емпіричні закономірності лінійчатого спектра атома водню, виражені у формулі Бальмера – Ридберга.
Ядерна модель атома Резерфорда.
Квантовий характер випромінювання й поглинання світла (теплове випромінювання й фотоефект).
Для можливості розв’язання виниклих утруднень Н. Бор (датський вчений) сформулював три постулати для водню й воднеподібних атомів – ядром із зарядом Ze і один електрон рухається навколо ядра.
I – й постулат – постулат стаціонарних станів:
У системі існують деякі стаціонарні стани, що не змінюються в часі без зовнішніх впливів. У цих станах атом не випромінює світла.
I I
–й постулат – правило квантування
орбіт:
I
–й постулат – правило квантування
орбіт:
У стаціонарному стані атома електрон, рухаючись по круговій орбіті із прискоренням, не випромінює світла, повинен мати дискретні (квантовані) значення моменту імпульсу
![]()
III – й постулат – правило орбіт:
Випромінювання випускається або поглинається у вигляді світлового кванта енергії при переході електрона з одного стаціонарного стану в інше.
Величина світлового кванта дорівнює різниці енергій стаціонарних станів, між якими відбувається перехід електрона
![]() ,
,
n > m –випромінювання фотона,
n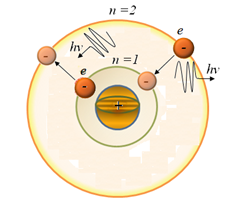 < m –
< m –
поглинання фотона.
Набір можливих дискретних частот
![]()
квантових переходів і визначають лінійчатий спектр атома.
Будова атома |
Атом - мікрочастинка, яка складається з ядра, що вміщує протони і нейтрони, і електронів, які утворюють зовнішню оболонку Хімічний елемент - вид атомів з однаковим зарядом ядра Ізотоп - вид атомів з однаковим масовим числом Масове число - загальна кількість протонів і нейтронів, що входять до ядра |
Квантові числа - параметри, що визначають електронну структуру і властивості електронів атома n - головне квантове число; визначає енергетичний рівень і енергію електрона n = 1, 2, ...[1]... ; l - орбітальне квантове число; визначає енергетичний підрівень, форму орбіталі і енергію електрона l = 0, 1, ...[1]... n-1; ml - магнітне квантове число; визначає просторову орієнтацію атомних орбіталей ml = -1... [1]...+1; ms - спінове квантове число; визначає власний механічний і магнітний момент електрона ms = -1/2 або +1/2 Кількість енергетичних підрівнів на енергетичному рівні дорівнює n Електронна ємність енергетичного рівня дорівнює 2n2 Кількість орбіталей на енергетичному підрівні дорівнює 2l + 1 Електронна ємність енергетичного підрівня дорівнює 2·(2l + 1) |
Принцип Паулі - в атомі не може бути двох або більше електронів з однаковим набором всіх чотирьох квантових чисел Правило Гунда - сумарне спінове число електронів на даному підрівні повинне бути максимальним Правило Клечковського - енергетичні підрівні заповнюються у порядку зростання величини n+l, а при рівних значеннях - у порядку зростання величини n. |
