7. Природа пластичности минералов. Пластические свойства породы. Параметры их характеризующие.
Пластические свойства пород проявляются при нагрузках, превышающих предел упругости породы, после снятия которых порода уже не полностью восстанавливает исходную форму и размеры.
Пластическая деформация в породах обусловлена внутризеренным и межзеренным скольжением (постепенное соскальзывание атомов в кристаллической решетке с одного на другой, сдвиг зерен по определенным плоскостям и направлениям под действием нагрузок). Значительную роль во внутризеренном скольжении играют дислокации — сдвиги одной части кристалла относительно другой или линии искажения, проходящие вдоль края лишней атомной плоскости. Однако дислокация, вышедшая на поверхность или границу зерна, в дальнейшем уже не принимает участия в пластической деформации. Плотность дислокаций внутри зерна уменьшается, и пластическая деформация затухает. Именно поэтому для поддержания деформирования в породе необходимо увеличивать напряжения.
Пластическая деформация происходит без нарушения сплошности тела. Однако довольно часто пластичность, рассматриваемая в породах, не совпадает с понятием идеальной пластичности, так как, строго говоря, ряд явлений, вызывающих в породах остаточные деформации (обжатие, смятие, взаимное перемещение блоков), следует отнести к разрушающим .
Если
связь между напряжением а и относительной
деформацией е в области пластической
деформации выразить через некоторый
коэффициент
,
то Е', называемый се кущи м модуле м
деформации , будет находиться в пределах
Предельный секущий модуль деформации — отношение прироста напряжений в пластической зоне (до момента разрушения породы) к полной пластической деформации
называется модулем пластичности.
Для идеального пластического тела Епл = 0.
Если
на рис. 3.9 соединить прямой линией
конечную точку графика (момент разрушения
образца) с началом координат, то
тангенс образовавшегося угла а' будет
называться модулем полной деформации
Он
равен отношению максимальных (разрушающих)
напряжении
к
полной относительной деформации образца
Пластичность горных пород зависит от их минерального состава. Наличие жестких кварцевых зерен и полевого шпата в породе уменьшает ее пластичность.
В углях наблюдается зависимость пластичности от содержания в них углерода. При переходе от слабометаморфизованных углей к антрацитам их пластичность уменьшается в 30 раз.
Характерно, что повышение пластичности в породах сопровождается, как правило, снижением их модуля упругости. В то же время коэффициент Пуассона с увеличением пластичности пород растет.
8. Физические теории прочности минералов. Теория прочности Гриффитса.
Прочность
породы определяется величиной критических
напряжений, при которых происходит ее
разрушение. Эти напряжения различны
для разных пород и для разных видов
приложенных нагрузок. Они носят названия
пределов прочности. Различают пределы
прочности пород при сжатии
,
растяжении
,
сдвиге
,
изгибе
и
т. д.
Разрушение — это разрыв связей между атомами и ионами в кристаллической решетке. Величины сил, необходимых для разрыва, зависят от типа межатомных связей и строения кристаллической решетки вещества.
Реальные значения предела прочности при растяжении в сотни и тысячи раз меньше теоретических. Причина таких расхождений кроется в том, что реальные тела обладают множеством различных дефектов. В кристалле — это точечные (вакансии) и линейные (дислокации) искажения кристаллической решетки. В породе— это границы зерен — плоскостные и поры — объемные искажения и нарушения строения породы!
В зависимости от масштаба разрушения породы преобладающее значение имеют те или другие виды дефектов.
Существует несколько масштабов (уровней) разрушения пород. Мегаскопический уровень разрушения характерен для взрывания массивов пород, сдвижений и обвалов их. В этом случае наиболее сильно на разрушаемости сказываются крупные трещины.
Микроскопический уровень разрушения характерен для измельчения полезных ископаемых в мельницах и, частично, при бурении скважин. На этой стадии происходит разрыв связей в кристаллах и зернах. При этом существенную роль играют дислокации и вакансии.
Прочность
пород, соответствующая той или иной
длительности воздействия нагрузки,
называется их длительной (текущей)
прочностью
.
С увеличением времени действия нагрузки
величина
падает по кривой, асимптотически
приближаясь к некоторому предельному
значению, называемому пределом длительной
прочности
,
(см. рис. 3.15). Для ряда глин и мергелей
Курской магнитной аномалии
=
0,5
Для
других пород предел длительной прочности
=
(0,7
0,8)
Между длительной прочностью глин и временем приложения нагрузки t установлена следующая эмпирическая зависимость:
где В — константа, характеризующая стойкость породы.
Отношение мгновенного предела прочности при сжатии к некоторому значению длительной прочности называется коэффициентом расслабления.
Теоретическая и техническая прочности. Теория Гриффитса
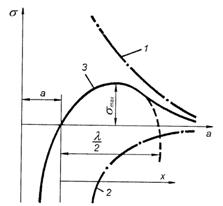
Рис.22.10
Для
того чтобы увеличить расстояние между
атомами, находящимися в равновесии, на
величину 
,
необходимо приложить растягивающее
напряжение. Считая силу взаимодействия
равной этому напряжению, его можно
приближенно выразить в виде гармонической
функции расстояния.
Значительное различие между теоретической и реальной прочностью материалов на современном уровне объясняется следующими факторами:
- значительными отклонениями от строгого, регулярного расположения атомов в кристаллической решетке материала, т.е. дефектностью структуры материала;
- технологическими нарушениями сплошности материала – трещинами.
Несоответствие между теоретической прочностью межатомных связей и экспериментальной прочностью натолкнуло английского ученого А.Гриффитса на мысль, что большое расхождение в прочностях объясняется наличием мелких трещин в однородном материале, которые приводят к большой концентрации напряжений в упругом состоянии.
Рассмотрим
бесконечную пластину единичной толщины
с центральной поперечной трещиной
длиной 2
.
Края трещины неподвижны, а напряжение
в ней равно 
(рис.22.3, а).
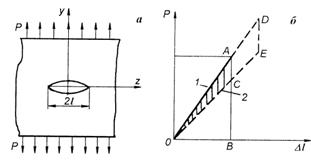
Рис.22.11
На
рис.22.11, б приведена
диаграмма «нагрузка-удлинение».
Запасенная в пластине упругая энергия
представлена площадью ОАВ.
Если длина трещины увеличится на
величину 
,
то жесткость пластины уменьшится (линия
ОС);
это означает, что нагрузка несколько
уменьшится, поскольку края пластины
неподвижны. Следовательно, упругая
энергия, запасенная в пластине, уменьшится
до величины, равной ОСВ.
Увеличение длины трещины от
до 
приведет
к высвобождению упругой энергии, равной
по величине площади ОАС.
Если пластина нагружена до более высокого напряжения, то при увеличении длины трещины на величину освободится большая энергия. Гриффитс предположил, что трещина будет расти лишь в том случае, если освобождаемая при этом энергия достаточна для обеспечения всех затрат энергии, связанных с этим ростом. В противном случае необходимо увеличить напряжение. Треугольник ODE иллюстрирует энергию, выделяемую при распространении трещины.
Условие, необходимое для роста трещины, следующее:
, (22.19)
где 
-
упругая энергия;
-
энергия, необходимая для роста трещины.
Основываясь
на расчетах, Гриффитс получил
выражение для 
в
виде
(22.20)
на
единицу толщины пластины, где 
-
модуль упругости первого рода.
Величину 
называют
скоростью высвобождения упругой энергии.
Поверхностная энергия пластины, связанная с наличием в ней трещины:
, (22.21)
где 
-
удельное поверхностное натяжение,
вводимое для твердого тела по аналогии
с таким же понятием для жидкости.
Энергию, расходуемую на распространение трещины, найдем как
. (22.22)
Приравнивая правые части (22.20) и (22.22), получим
. (22.23)
Вследствие этого возникает хрупкое разрушение, которое характеризуется коэффициентом интенсивности напряжений
. (22.24)
Из
анализа уравнений (22.20) и (22.22) видно, что
трещина, достигнув критической длины 
при
напряжении 
,
становится неустойчивой.
Этот коэффициент имеет размерность Н/мм3/2.
Графическое изображение критического состояния представлено на рис.22.12. Из графика видно, что при напряжении меньше критического трещина развиваться не будет. При достижении критического напряжения трещина начинает развиваться неустойчиво.
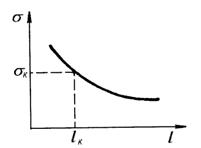
Рис.22.12