26)Коэффициент корреляций.Линия регрессии.
ρ
— мера силы линейной связи между случайными
величинами X и
У: 
,
где ЕХ
— математическое
ожидание X;
DX — дисперсия X,
EY —математическое
ожидание У; DY
— дисперсия
У; — 1 ≤ ρ ≤ 1. Если X,
Y линейно
связаны, то ρ = ± 1. Для независимых
случайных величин ρ = 0.
Если X, У
распределены, нормально и ρ = 0, то эти
случайные величины независимы.
Если та формула не нравится еще такая есть!Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными. Он вычисляется следующим образом:
,
где n – количество наблюдений, x – входная переменная, y – выходная переменная. Значения коэффициента корреляции всегда расположены в диапазоне от -1 до 1
Функция φ(х)=М(Y/Х=х), описывающая изменение условного математического ожидания случайной переменной Y при изменении значений х переменной Х, называется функцией регрессии, а ее график – линией регрессии.
27)Функция комплексного переменного и её свойства
Комплексные числа мы условились изображать точками плоскости, где задана прямоугольная система координат.
Дадим понятие функции от комплексного переменного.
Пусть
даны две плоскости комплексных
чисел 
и 
(рис.
129). Рассмотрим некоторое множество
точек 
в
плоскости 
и
множество 
в
плоскости 
.
Если каждому числу 
по
некоторому закону поставлено в
соответствие определенное комплексное
число 
,
то говорят, что на множестве
задана
однозначная функция комплексного
переменного, отображающая множество
в
множество
.
Символически это обозначают так:
Множество
называют
областью определения функции 
.
Если каждая точка множества
является
значением функции, то говорят, что
-
область значений этой функции или образ
множества
при
помощи функции 
.
В этом случае говорят еще, что
функция 
отображает
на
.
Функцию можно записать в виде
,
где
,
,
-
действительные функции от переменных 
.
Если каждому соответствует несколько разных значений , то функция называется многозначной.
Понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции действительного переменного, необходимо лишь всюду вместо абсолютной величины писать модуль комплексного числа.
Говорят, что функция
имеет
предел в точке 
,
равный числу 
,
если
.
(1)
В этом случае пишут
.
На
языке функций 
и 
свойство
(1) записывается в виде равенства
(2)
или, что все равно, в виде двух равенств
, 
.
(3)
Для
комплексных функций
и 
имеют
место свойства, аналогичные соответствующим
свойствам действительных функций:
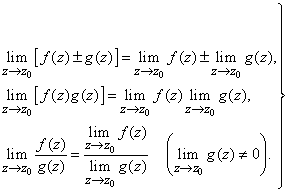(4)
Как обычно, формулы (4) надо понимать в том смысле, что если пределы, стоящие в их правых частях, существуют, то существуют также пределы, стоящие в их левых частях, и выполняется соответствующее равенство.
Функция называется непрерывной в точке , если для нее выполняется свойство
, 
, 
.
(5)
Таким образом, непрерывная в точке функция должна быть определена в окрестности этой точки, в том числе и в ней самой и должно выполняться равенство (5). Равенство (5) эквивалентно двум равенствам:
, 
.
Следовательно,
непрерывность
в
точке
эквивалентна
непрерывности функций
и
в
точке 
.
Из свойств (4) следует, что сумма, разность, произведение и частное непрерывных в точке комплексных функций и есть непрерывная функция в этой точке.