20)Понятия точечной и интервальной оценки. Точечные статистические оценки

Статистическая оценка неизвестного параметра генеральной совокупности одним числом называется точечной. Рассмотрим следующие точечные оценки: смещенные и несмещенные, эффективные и состоятельные.

Для того чтобы статистические оценки давали хорошие приближения оцениваемых параметров, они должны удовлетворять определенным требованиям. Укажем эти требования. Пусть   есть статистическая оценка неизвестного параметра   теоретического распределения. Допустим, что по выборке объема   найдена оценка  . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку   и т. д. Получим числа  , которые будут различаться. Таким образом, оценку   можно рассматривать как случайную величину, а числа   — как возможные ее значения.

Если оценка   дает приближенное значение   с избытком, то найденное по данным выборок число   будет больше истинного значения  . Следовательно, и математическое ожидание (среднее значение) случайной величины   будет превышать  , то есть  . Если   дает приближенное значение   с недостатком, то  .

.

Интервальные оценки

Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр.

Доверительным интервалом   для параметра   называется такой интервал, относительно которого с заранее выбранной вероятностью  , близкой к единице, можно утверждать, что он содержит неизвестное значение параметра  , то есть . Чем меньше для выбранной вероятности число  , тем точнее оценка неизвестного параметра  . И, наоборот, если это число велико, то оценка, проведенная с помощью данного интервала, малопригодна для практики. Так как концы доверительного интервала зависят от элементов выборки, то значения   и   могут изменяться от выборки к выборке. Вероятность   принято называть доверительной (надежностью). Обычно надежность оценки задается наперед, причем в качестве   берут дчисло, близкое к единице

21)Доверительные интервалы для матожидания

Доверительным называется интервал, который с заданной надежностью   покрывает оцениваемый параметр.

Для оценки математического ожидания   случайной величины  , распределенной по нормальному закону, при известном среднем квадратическом отклонении   служит доверительный интервал

где   - точность оценки,   - объем выборки,   - выборочное среднее,   - аргумент функции Лапласа, при котором 

22)Статическая проверка статических гипотез .Ошибки 1-го и 2-го рода.

Проверка гипотез - это процедура сопоставления высказанного предположения (гипотезы) с выборочными данными.

Задачи статистической проверки гипотез ставятся в следующем виде: относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н. Из этой генеральной совокупности извлекается выборка. Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос о том, следует ли отклонить гипотезу Н или принять ее.Одну из гипотез выделяют в качестве основной (или нулевой) и обозначают  , а другую, являющуюся логическим отрицанием  , т.е. противоположную  – в качестве конкурирующей (или альтернативной) гипотезы и обозначают  .

Гипотезу, однозначно фиксирующую распределение наблюдений, называют простой (в ней идет речь об одном значении параметра), в противном случае – сложной.

Имея две гипотезы  и  , надо на основе выборки  принять либо основную гипотезу  , либо конкурирующую  .

Правило, по которому принимается решение принять или отклонить гипотезу  (соответственно, отклонить или принять  ), называется статистическим критерием (или просто критерием) проверки гипотезы  .

Проверку гипотез осуществляют на основании результатов выборки  , из которых формируют функцию выборки  , называемой статистикой критерия.

Основной принцип проверки гипотез состоит в следующем. Множество возможных значений статистики критерия  разбивается на два непересекающихся подмножества: критическую область S, т.е. область отклонения гипотезы  и область  принятия этой гипотезы. Если фактически наблюдаемое значение статистики критерия (т.е. значение критерия, вычисленное по выборке:  ) попадает в критическую область S, то основная гипотеза  отклоняется и принимается альтернативная гипотеза  ; если же  попадает в  , то принимается  , а  отклоняется.

При проверке гипотезы может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.Ошибка первого рода состоит в том, что отвергается нулевая гипотеза  , когда на самом деле она верна.

Ошибка второго рода состоит в том, что отвергается альтернативная гипотеза  , когда она на самом деле верна.Вероятность ошибки 1-го рода (обозначается через  ) называется уровнем значимости критерия.Вероятность ошибки 2-го рода обозначается через  , т.е.  .Величину  , т.е. вероятность недопущения ошибки 2-го рода (отвергнуть неверную гипотезу  , принять верную  ), называется мощностью критерия.

Методика проверки гипотез сводится к следующему:

1. Располагая выборкой  , формируют нулевую гипотезу  и альтернативную  .

2. В каждом конкретном случае подбирают статистику критерия  .

3. По статистике критерия  и уровню значимости  определяют критическую область S (и  ). Для ее отыскания достаточно найти критическую точку 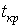 , т.е. границу (или квантиль), отделяющую область S от  .

4. Границы областей определяются, соответственно, из соотношений: 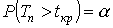 , для правосторонней критической области S (рис. 7);  , для левосторонней критической области S (рис. 8); 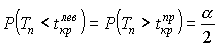 , для двусторонней критической области S (рис. 9).

5. Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую приведенным выше соотношениям.

6. Для полученной реализации выборки 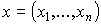 подсчитывают значение критерия, т.е.  .

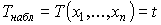7. Если 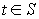 (например,  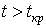для правосторонней области S), то нулевую гипотезу  отвергают; если же