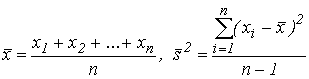17)Эмпирические функции. Эмпирические частоты.
Эмпирической функцией выборки (функцией распределения выборки) называется функция
Fn(x)= |
nx |
|
|
n |
|
, которую можно записать в следующем виде:
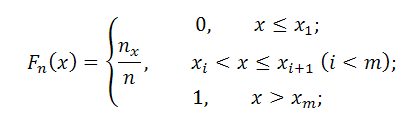
Данная функция непрерывная, кусочно-постоянна и изменяется в каждой точке хi, где хi — варианта рассматриваемого статистического распределения.
Эмпирические частоты получают в результате опыта (наблюдения). Теоретические частотырассчитывают по формулам. Для нормального закона распределения их можно найти следующим образом:
где 
—
сумма эмпирических частот; 
—
разность между двумя соседними
вариантами; 
—
выборочное среднеквадратическое
отклонение; 
; 
—
выборочная средняя арифметическая;
1 8) Определение неизвестных параметров.
C
помощью гистограммы мы можем приближенно
построить график плотности распределения
случайной величины 
.
Вид этого графика часто позволяет
высказать предположение о плотности
распределения вероятностей 
случайной
величины
.
В выражение этой плотности распределения
обычно входят некоторые параметры,
которые требуется определить из опытных
данных.
Остановимся на
том частном случае, когда плотность
распределения
зависит
от двух параметров.
Итак,
пусть x1,
x2,
..., xn -
наблюдаемые значения непрерывной
случайной величины
,
и пусть ее плотность распределения
вероятностей зависит от двух неизвестных
параметров A и B,
т.е. имеет вид 
.
Один из методов нахождения неизвестных
параметров A и B состоит
в том, что их выбирают таким образом,
чтобы математическое ожидание и
дисперсия теоретического распределения
совпали с выборочными средними
значением 
и
дисперсией 
:
|
(66) |
где
|
(67) |
Из двух полученных уравнений (66) находят неизвестные параметры A и B. Так, например, если случайная величина подчиняется нормальному закону распределения вероятностей, то ее плотность распределения вероятностей
зависит
от двух параметров a и 
.
Эти параметры, как мы знаем, являются
соответственно математическим ожиданием
и средним квадратическим отклонением
случайной величины
;
поэтому равенства (66)
запишутся так:
|
(68) |
Следовательно, плотность распределения вероятностей имеет вид
19)Статистическая оценка параметров распределения Оценка - это приближение значений искомой величины, полученное на основании результатов выборочного наблюдения. Оценки являются случайными величинами. Они обеспечивают возможность формирования обоснованного суждения о неизвестных параметрах генеральной совокупности. Примером оценки генеральной средней является выборочная средняя генеральной дисперсии – выборочная дисперсия и т.д.Для того чтобы оценить насколько «хорошо» оценка отвечает соответствующей генеральной характеристике разработаны 4 критерия: состоятельность, несмещенность, эффективность и достаточность. Этот подход основывается на том, что качество оценки определяется не по ее отдельным значениям, а по характеристикам ее распределения как случайной величины. Несмещенность оценки проявляется в том, что ее математическое ожидание при любом объеме выборки равно значению оцениваемого параметра в генеральной совокупностиСостоятельность статистических оценок проявляется в том, что с увеличением объема выборки оценка все больше и больше приближается к истинному значению оцениваемого параметра или, как говорят, оценка сходится по вероятности к искомому параметру, или стремится к своему математическому ожиданию. Лишь состоятельные оценки имеют практическую значимость. Рассмотрим оценку θn числового параметра θ, определенную при n = 1, 2, … Оценка θn называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра θ при безграничном возрастании объема выборки. Состоя́тельная оце́нка в математической статистике — это точечная оценка, сходящаяся по вероятности к оцениваемому параметру.
Статистика 
называется состоятельной
оценкой параметра
параметра 
,
если с ростом размера выборки оценка
стремиться по вероятности к оцениваемому
параметру:
при
любом сколь угодно малом 
Статистика называется несмещенной оценкой параметра , если математическое ожидание оценки равняется оцениваемому параметру:
