15) Теорема Чебышева. Предельные теоремы . Центральная предельная теорема.

Теорема Чебышёва в теории вероятностей — теоретическая основа закона больших чисел; широкое обобщение теоремы Бернулли; первое строгое доказательство дал П.Л.Чебышёв (1867);

В работе П.Л.Чебышёва «О средних величинах» (1867) была установлена

Теорема (Теорема Чебышёва). Для независимых случайных величин   соотношение

(при любом   и  ) верно при весьма общих предположениях:

Центральная предельная теорема

Первый вариант этой теоремы был доказан в 1912 г. А.М.Ляпуновым. В настоящее время имеется несколько формулировок этой теоремы, различающихся условиями, которые накладываются на случайные величины. Мы приведём простейший вариант центральной предельной теоремы для одинаково распределённых независимых случайных величин.

Пусть   последовательность одинаково распре­делённых случайных величин с математическими ожиданиями   и дисперсиями  .

ТЕОРЕМА. Если случайные величины   независимы и  , то при достаточно большом n закон распределения суммы   будет сколь угодно близок к нормальному закону распределения  .

Так как в условиях теоремы случайные величины независимы, то

т.е. в условиях теоремы сумма   имеет закон распределения близкий к  .Так' как  na и   с ростом п, возрастают, то удобнее рассматривать не просто суммы  , а нормированные суммы  . Такие суммы при   имеют закон распределения  .

Интегральная теорема Лапласа. Пусть X есть число наступлений собы­тия в п независимых опытах, в каждом из которых вероятность появления события равна  .Тогда при достаточно больших n вероятность того, что событие появится от   до   раз равна

, где q=1-p, Ф(х) – функция Лапласа.

Эта теорема является следствием из, центральной предельной теоремы, хотя и была доказана гораздо раньше неё. В самом деле, число появлений события в n независимых опытах можно представить следующим образом

число успехов,

где   - число появлений события в i -м опыте, причём ранее было показано, что   и  . Т.е. X является суммой большого числа независимых случайных величин   и  . Условия центральной предельной теоремы выполнены, X имеет закон распределения близкий к 

16)Предмет и задачи математической статистики. Выборочный метод . Вариационный ряд.

Математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных. Любая наука решает в порядке возрастания сложности и важности следующие задачи:

1) описание явления;

2) анализ и прогноз;

3) поиск оптимального решения.

Такого рода задачи решает и математическая статистика: 

1) систематизировать полученный статистический материал; 

2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины; 

3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения. 

Одной из задач третьего типа является задача проверки правдоподобия гипотез. Она может быть сформулирована следующим образом: имеется совокупность опытных данных, относящихся к одной или нескольким случайным величинам. Необходимо определить, противоречат ли эти данные той или иной гипотезе, например, гипотезе о том, что исследуемая случайная величина распределена по определенному закону, или две случайные величины некоррелированы (т.е. не связаны между собой) и т.д. В результате проверки правдоподобия гипотезы она либо отбрасывается, как противоречащая опытным данным, либо принимается, как приемлемая.

Таким образом, математическая статистика помогает экспериментатору лучше разобраться в полученных опытных данных, оценить, значимы или нет определенные наблюденные факты, принять или отбросить те или иные гипотезы о природе рассматриваемого явления

Предметом изучения теории вероятностей и математической статистики являются случайные события, величины и функции.

Выборочный метод

Выборочный метод - основной метод математической статистики, состоящий в принятии статистических решений на основании выборки. Различают:  - случай предварительного планирования объема выборки; и  - случай последовательного анализа, когда необходимый объем выборки выясняется в процессе эксперимента.

Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины

р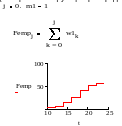 авные между собой элементы выборки нумеруются в произвольном порядке; элементы вариационного ряда называются порядковыми (ранговыми) статистиками; число λ_m = m / nназывается рангом порядковой статистики 

Вариационный ряд используется для построения эмпирической функции распределения. Если элементы вариационного ряда независимы и имеют общую плотность распределения f, то совместная плотность распределения элементов вариационного ряда имеет вид