
- •10)Правило трех сигм. Распределение Пирсона, Стьюдента.
- •11) Функция распределения и плотность распределения вероятностей двумерной случайной величины
- •12) Числовые характеристики случайной двумерной величины.
- •13) Коэффициент корреляции, линии регрессии.
- •14)Закон больших чисел . Неравенства Чебышева и Маркова.
- •15) Теорема Чебышева. Предельные теоремы . Центральная предельная теорема.
- •16)Предмет и задачи математической статистики. Выборочный метод . Вариационный ряд.
- •17)Эмпирические функции. Эмпирические частоты.
- •1 8) Определение неизвестных параметров.
- •20)Понятия точечной и интервальной оценки. Точечные статистические оценки
- •21)Доверительные интервалы для матожидания
- •22)Статическая проверка статических гипотез .Ошибки 1-го и 2-го рода.
- •23)Построение теоретического закона распределения по данному вариационному роду
- •25)Линейная корреляция.Функциональная,статистическая и корреляционные зависимости.
- •26)Коэффициент корреляций.Линия регрессии.
- •27)Функция комплексного переменного и её свойства
- •28)Производная функций комплексного переменного.Условие Коши-Римана.Аналитические функции.
1)Случайной
величиной
называется функция![]() , измеримая относительно
, измеримая относительно![]() и борелевской σ-алгебры на
и борелевской σ-алгебры на
![]() .
Случайную величину можно определить
и другим эквивалентным способом. Функция
называется случайной величиной, если
для любых вещественных чисел
.
Случайную величину можно определить
и другим эквивалентным способом. Функция
называется случайной величиной, если
для любых вещественных чисел
![]() и
и
![]() множество
множество
![]() событий , таких что
событий , таких что![]() , принадлежит
.
, принадлежит
.
Случайная
величина
![]() называется дискретной
случайной величиной, если она принимает
не более чем счетное число значений.
Задание дискретной случайной величины
по определению равносильно заданию
закона распределения случайной величины
в следующем виде
называется дискретной
случайной величиной, если она принимает
не более чем счетное число значений.
Задание дискретной случайной величины
по определению равносильно заданию
закона распределения случайной величины
в следующем виде![]()
![]() где
где![]()
Распределение
случайной величины
называется непрерывным,
а сама случайная величина - непрерывной
случайной величиной, если для любого![]() где
где![]() - интегрируемая по Лебегу функция.
Функция
- интегрируемая по Лебегу функция.
Функция
![]() называется плотностью распределения
случайной величины
.
называется плотностью распределения
случайной величины
.
Распределением
случайной величины
называется вероятностная мера
![]() на множестве борелевских подмножеств
на множестве борелевских подмножеств
![]()
Cлучайная
величина
![]() имеет дискретное распределение, если
имеет дискретное распределение, если
существует
конечный или счётный набор чисел
![]() такой, что
такой, что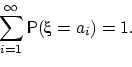 Cлучайная величина
имеет абсолютно непрерывное распределение,
если существует неотрицательная
функция
Cлучайная величина
имеет абсолютно непрерывное распределение,
если существует неотрицательная
функция![]() такая, что для любого борелевского
множества
такая, что для любого борелевского
множества![]() имеет место равенство:
имеет место равенство:
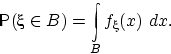
2)Функцией
распределения случайной величины
мы назвали функцию
![]() функция,
характеризующая распределение случайной
величины или случайного вектора.
Основные свойства:
функция,
характеризующая распределение случайной
величины или случайного вектора.
Основные свойства:
она
не убывает: если![]() , то
, то![]() ; cуществуют пределы
; cуществуют пределы![]() и
и
![]() ;
она в любой точке непрерывна слева
;
она в любой точке непрерывна слева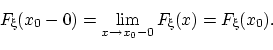
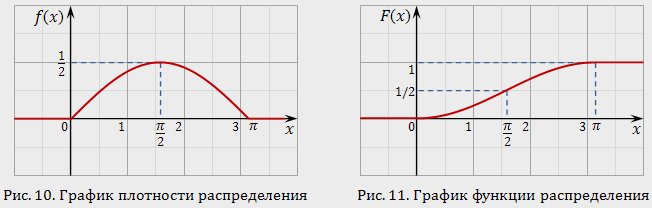
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Основные свойства плотности распределения:
1.
Плотность распределения есть
неотрицательная функция:
![]()
Это
свойство непосредственно вытекает из
того, что функция распределения![]() есть неубывающая функция. 2. Условие
нормировки:
есть неубывающая функция. 2. Условие
нормировки:
 Это
свойство следует из формулы
Это
свойство следует из формулы
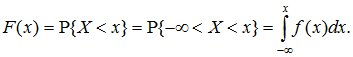 ,
если положить в ней x=∞.
,
если положить в ней x=∞.
Геометрически основные свойства плотности f(x) интерпретируются так:вся кривая распределения лежит не ниже оси абсцисс;полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Функция
распределения
,
как всякая вероятность, есть величина
безразмерная. Размерность плотности
распределения![]() , как видно из формулы, обратна размерности
случайной величины.
, как видно из формулы, обратна размерности
случайной величины.
3) Числовые характеристики одномерных случайных величин
Математическим
ожиданием дискретной случайной величины
называется сумма произведений всех ее
возможных значений на соответствующие
вероятности.
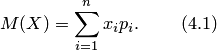
Для непрерывной случайной величины математическое ожидание
![]() возможные
значения которой принадлежат отрезку
возможные
значения которой принадлежат отрезку![]()
![]()
Свойства
математического ожидания:
суммы двух случайных величин равно
сумме их математических ожиданий:
![]() произведения двух независимых случайных
величин равно произведению их
математических ожиданий:
произведения двух независимых случайных
величин равно произведению их
математических ожиданий:
![]() МО постоянной величины равно самой
постоянной:
МО постоянной величины равно самой
постоянной:
![]() Постоянный множитель случайной
величины можно вынести за знак
математического ожидания:
Постоянный множитель случайной
величины можно вынести за знак
математического ожидания:
![]() МО отклонения
случайной величины от ее математического
ожидания равно нулю
МО отклонения
случайной величины от ее математического
ожидания равно нулю![]()
Модой
![]() дискретной случайной величины называется
наиболее вероятное ее значение. Модой
непрерывной случайной величины
называется такое ее значение, которому
соответствует наибольшее значение
плотности распределения. Геометрически
моду интерпретируют как абсциссу точки
глобального максимума кривой
распределения
дискретной случайной величины называется
наиболее вероятное ее значение. Модой
непрерывной случайной величины
называется такое ее значение, которому
соответствует наибольшее значение
плотности распределения. Геометрически
моду интерпретируют как абсциссу точки
глобального максимума кривой
распределения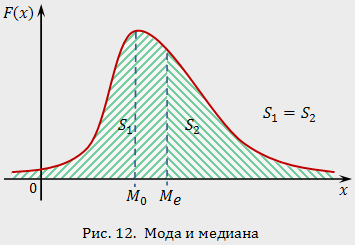
Медианой
![]() случайной величины называется
такое ее значение, для которого
справедливо равенство
случайной величины называется
такое ее значение, для которого
справедливо равенство![]() Математическое ожидание квадрата
отклонения случайной величины от ее
математического ожидания,
которое называют дисперсией случайной
величины
Математическое ожидание квадрата
отклонения случайной величины от ее
математического ожидания,
которое называют дисперсией случайной
величины
![]() и обозначают
и обозначают![]()
![]()
![]()
среднее
квадратическое отклонение случайной
величины
![]()
Свойства
дисперсии:1.
суммы двух независимых случайных
величин равна сумме дисперсий этих
величин
![]()
2.разности
между математическим ожиданием квадрата
случайной величины и квадратом ее
математического ожидания![]()
3.
Дисперсия
постоянной величины равна нулю![]() 4.
Постоянный множитель случайной величины,
можно выносить за знак дисперсии,
предварительно возведя его в квадрат
4.
Постоянный множитель случайной величины,
можно выносить за знак дисперсии,
предварительно возведя его в квадрат![]() 5.
Дисперсия произведения двух независимых
случайных величин
и
5.
Дисперсия произведения двух независимых
случайных величин
и
![]() :
:![]()
4)
если случайная величина X задана
плотностью распределения
![]() , то вероятность того, что X примет
значение, принадлежащее интервалу
(a,b), такова:
, то вероятность того, что X примет
значение, принадлежащее интервалу
(a,b), такова:
![]()
Начальным
моментом порядка
![]() случайной величины
случайной величины
![]() называют математическое ожидание
величины
называют математическое ожидание
величины
![]() :
:![]()
Центральным
моментом порядка
случайной
величины
называют математическое ожидание
величины![]() :
:
![]()
Для
дискретных случайных величин![]() ;
;![]()
Для
непрерывного распределения
![]()
![]()
5)
Геометрическое
распределениеСо
схемой испытаний Бернулли можно связать
еще одну случайную величину x - число
испытаний до первого успеха. Эта величина
принимает бесконечное множество
значений от 0 до +
![]() и
ее распределение определяется формулой
и
ее распределение определяется формулой
pk
= P(x= k) = qk-1 p, 0 <p <1, k=1, 2, … ,
![]() ,
,
![]() ,
,
![]()
Гипергеометрическое распределениеВ партии из N изделий имеется M (M < N) доброкачественных и N - M дефектных изделий. Если случайным образом из всей партии выбрать контрольную партию из n изделий, то число доброкачественных изделий в контрольной партии - случайная величина, которую обозначим x. Распределение такой случайной величины называется гипергеометрическим и имеет вид:
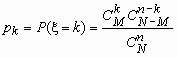 ,
k
= 0, 1, …, min(n,M),
,
k
= 0, 1, …, min(n,M),
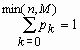 ,
,
![]()
![]()
6) Биномиальное распределение называют законы распределения случайной величины Х числа появления некоторого события в n опытах если вероятность р появления события в каждом опыте постоянна
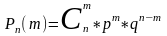
Сумма вероятностей представляют собой бином Ньютона

Для определения числовых характеристик в биномиальное распределение подставить вероятность которая определяется по формуле Бернули.
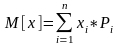
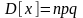
При биномиальном распределении дисперсия равна мат. Ожиданию умноженному на вероятность появления события в отдельном опыте.
Пуассоновским называют закон распределения дискретной случайной величины Х числа появления некоторого события в n-независимых опытах если вероятность того, что событие появится ровно m раз определяется по формуле.
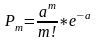 a=np
n-число
проведенных опытов, р-вероятность
появления события в каждом опыте В
теории массового обслуживания параметр
пуассоновского распределения определяется
по формуле
a=np
n-число
проведенных опытов, р-вероятность
появления события в каждом опыте В
теории массового обслуживания параметр
пуассоновского распределения определяется
по формуле
а=λt , где λ - интенсивность потока сообщений t-время
Необходимо отметить, что пуассоновское распределение является предельным случаем биномиального, когда испытаний стремится к бесконечности, а вероятность появления события в каждом опыте стремится к 0.
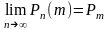
Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.
7) Равномерное распределение (непрерывное) закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке [-0,5; 0,5]), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Плотность
распределения:
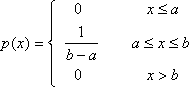 Числовые характеристики:
Числовые характеристики:
![]() ,
,
![]() ,
,
![]()
График плотности вероятностей:
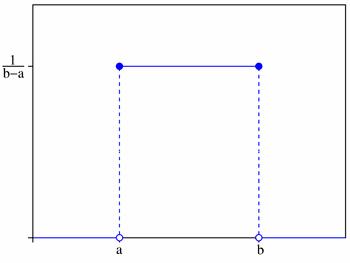
8) Показательное (экспоненциальное распределение)
Показательным называют распределение непрерывной случайной величины Х которое описывается следующей дифференциальной функцией
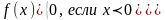
Экспоненциальное распределение для непрерывных случайных величин является аналогом распределения Пуассона для дискретных случайных величин и имеет следующий вид.
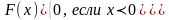
вероятность попадания случайной величины Х на интервал (α;β)
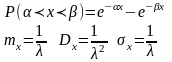
Следует отметить, что время безотказной работы удовлетворяется именно показательному закону, а поэтому это понятие часто используется в понятии надежности.
9) Нормальный закон распределения (закон Гаусса) называется распределение случайной величины Х если ф-ция плотности распределения
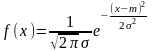

Полученное выражение через элементарные функции не может быть выражено, такая функция так называемый интеграл вероятности для которой составлены таблицы, чаще всего в качестве такой функции используют

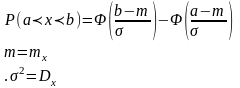
Часто по условию
задачи необходимо определить вероятность
попадания случайной величины Х на
участок симметричный математическому
ожиданию.

Правило трех сигм это правило часто используется для подтверждения или отбрасывания гипотезы о нормальном распределении случайной величины.
10)Правило трех сигм. Распределение Пирсона, Стьюдента.
Правило
трёх сигм (![]() ) —
практически все значения нормально
распределённой случайной
величины лежат в интервале
) —
практически все значения нормально
распределённой случайной
величины лежат в интервале ![]() .
Более строго — приблизительно с
99,73 % вероятностью значение нормально
распределённойслучайной
величины лежит в указанном интервале
(при условии, что величина
.
Более строго — приблизительно с
99,73 % вероятностью значение нормально
распределённойслучайной
величины лежит в указанном интервале
(при условии, что величина ![]() истинная,
а не полученная в результате обработки
выборки).
истинная,
а не полученная в результате обработки
выборки).
Если
же истинная величина
неизвестна,
то следует пользоваться не ![]() ,
а s.
Таким образом, правило трёх сигм
преобразуется в правило трёх s
,
а s.
Таким образом, правило трёх сигм
преобразуется в правило трёх s
Т .е.
вероятность того, что случайная величина
отклонится от своего математического
ожидание на величину, большую чем
утроенное среднее квадратичное
отклонение, практически равна нулю.
.е.
вероятность того, что случайная величина
отклонится от своего математического
ожидание на величину, большую чем
утроенное среднее квадратичное
отклонение, практически равна нулю.
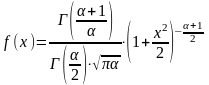
![]()

 -
N(0,1)
-
N(0,1)
n-
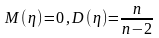
Распределение
Пирсона ![]() (хи
- квадрат) – распределение случайной
величины
(хи
- квадрат) – распределение случайной
величины
![]()
где случайные величины X1, X2,…, Xn независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.
Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных [8, 9, 11, 16].
Распределение t Стьюдента – это распределение случайной величины
![]()
где случайные величины U и X независимы, U имеет распределение стандартное нормальное распределениеN(0,1), а X – распределение хи – квадрат с n степенями свободы. При этом n называется «числом степеней свободы» распределения Стьюдента.
11) Функция распределения и плотность распределения вероятностей двумерной случайной величины
Фу́нкция
распределе́ния в теории
вероятностей —
функция, характеризующая распределение
случайной величины или
случайного вектора. При соблюдении
известных условий полностью определяет
случайную величину.
Пусть дано вероятностное
пространство ![]() ,
и на нём определена случайная
величина
,
и на нём определена случайная
величина ![]() с
распределением
с
распределением ![]() .
Тогда функцией распределения случайной
величины
называется функция
.
Тогда функцией распределения случайной
величины
называется функция ![]() ,
задаваемая формулой:
,
задаваемая формулой:
.
То
есть функцией распределения (вероятностей)
случайной величины
называют
функцию ![]() ,
значение которой в точке
,
значение которой в точке ![]() равно
вероятности события
равно
вероятности события ![]() ,
то есть события, состоящего только из
тех элементарных исходов, для которых
,
то есть события, состоящего только из
тех элементарных исходов, для которых ![]() .
.
Плотностью совместного распределения вероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения.
![]()
Если известна плотность распределения, то функция распределения может быть легко найдена по формуле:
![]()
Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности равен единице.
![]()
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины.
![]()
![]()
![]()
