§ 4 Теорема Кориолиса

Найдем зависимость между относительным, переносным и абсолютным движениями точки. Из равенства (теорема о сложении скоростей) получим

Производные здесь определяют изменение каждого из векторов при абсолютном движении. Эти изменения слагаются в общем случае из изменений при относительном и при переносном движениях, что ниже будет доказано. Следовательно, если изменения, которые векторы получают при относительном движении, отмечать индексом «1», а при переносном индексом «2», то предыдущее равенство примет вид

+ (1)

Но по определению относительное ускорение характеризует изменение относительной скорости только при относительном движении, движение осей Oxyz, т.е. переносное движение при этом во внимание не принимается. Поэтому

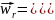
В свою очередь, переносное ускорение характеризует изменение переносной скорости, только при переносном движении w_е= w_m, где m – точка, неизменно связная с Oxyz и, следовательно, получающая ускорение только при движении вместе с этими осями, т.е. при переносном движении. Поэтому

=

В результате из равенства (1) получим

= + + (2)

Введем обозначение

= (3)

Величина , характеризующая изменение относительной скорости точки при переносном движении и переносной скорости в ее относительном движении, называется поворотным, или кориолисовым, ускорением точки. В результате равенство (2) примет вид

= + +

Эта формула выражает теорему о сложении ускорений.

Теорема Кориолиса

При сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и кориолисова.

§ 5 Примеры

П усть тело вращается вокруг неподвижной оси z. По поверхности его движется точка М. скорость этого движения – относительная скорость а скорость вращения тела –угловая скорость переносного движения . Ускорение Кориолиса

направлено перпендикулярно этим двум векторам, по правилу направления вектора векторного произведения. Так показано на рисунке. Вектор таким образом: вектор относительной скорости спроектирован на плоскость перпендикулярную оси переносного вращения и затем эта проекция повернута на 90 градусов в плоскость направления переносного вращения. Таким образом положение проекции вектора указывает направление кориолисова ускорения.

Литература

1. Бутенин И.В., Лунц Я.Л. , Меркин Д.Р. Курс теоретической механики. Т. 1 : Статика и кинематика.– М.: Наука, 1985.– 240 с.

2. Яблонский А.А. Курс теоретической механики. Ч. I : Статика. Кинематика.– М.: Высш. школа, 1984.– 343 с.

3. Попов М.В. Теоретическая механика. Краткий курс.– М.: Наука, 1986.– 336 с.

4. Теоретическая механика. Терминология, вып. 90.– М.: Наука, 1977.– 46 с.

5. Ільчишина Д.І., Шальда Л.М. Теоретична механіка.– К.: УМК ВО, 1991.– 252 с.