§ 2 Сложное движение точки

В ряде случаев при реше­нии задач механики оказывается целесообразным (а иногда и не­обходимым) рассматривать движение точки (или тела) одновременно по отношению к двум системам отсчета, из которых одна считается основной или условно неподвиж­ной, а другая определенным образом движется по отношению к первой. Движение, совершаемое при этом точкой (или телом), называют со­ставным или сложным. Например, шар, катящийся по палубе движу­щегося парохода, можно считать совершающим по отношению к бе­регу сложное движение, состоящее из качения по отношению к палубе (подвижная система отсчета), и движение вместе с палубой парохода по отношению к берегу (не­подвижная система отсчета). Таким путем сложное движение шара разлагается на два более простых и более легко исследуемых.

Рассмотрим точку М, движущуюся по отношению к подвижной системе отсчета Oxyz, которая в свою очередь как-то движется отно­сительно другой системы отсчета О₁x₁y₁z₁, которую называем основ­ной или условно неподвижной (рис.1). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не по­казанным. Введем следующие определения.

1 . Движение, совершаемое точкой М по отношению к подвиж­ной системе отсчета называется относительным движением (такое движение будет видеть наблюдатель, связанный с этими осями и перемещающийся вместе с ними). Траектория АВ, описываемая точкой в относительном движении, называется относи­тельной траекторией. Скорость точки М по отношению к осям Oxyz называется относительной

скоростью (обозначается v_r), a ускорение - относительным ускорением (обозначается w_r). Из определения следует, что при вычислении  v_r и  w_r можно движение осей Oxyz во внимание не принимать (рассматривать их как непод­вижные). 2. Движение, совершаемое подвижной системой отсчета Oxyz по отно­шению к неподвижной системе О₁x₁y₁z₁ , является для точки М пере­носным движением.

Скорость той неизменно связанной с подвижными осями Oxyz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент (обозначается v_е ), а ускорение этой точки m - переносным ускорением точки М (обозначается w_е). Таким образом,

V_е=V_m, w_е=w_m.

Если представить себе, что относительное движение точки про­исходит по поверхности (или внутри) твердого тела, с которым жестко связаны подвижные оси Oxyz, то переносной скоростью (или ускорением) точки М в данный момент времени будет скорость (или ускорение) той точки т тела, с которой в этот момент совпадает точка М.

3. Движение, совершаемое точкой по отношению к неподвижной системе отсчета О₁x₁y₁z₁, называется абсолютным или сложным. Траектория CD этого движения называется абсолютной траекто­рией, скорость - абсолютной скоростью (обозначается v_а) и ускорение - абсолютным ускорением (обозначается w_а).

§ 3 Ускорение Кориолиса

Ускорение Кориолиса – часть полного ускорения точки, появляющаяся при сложном движении, когда переносное движение (движение подвижной системы отсчета) не является поступательным. Оно появляется в следствии изменения относительной скорости точки v_r при переносном движении и переносной скорости при относительном движении точки. Численно ускорение Кориолиса:

W_C=2w_ev_rsin

где (w_e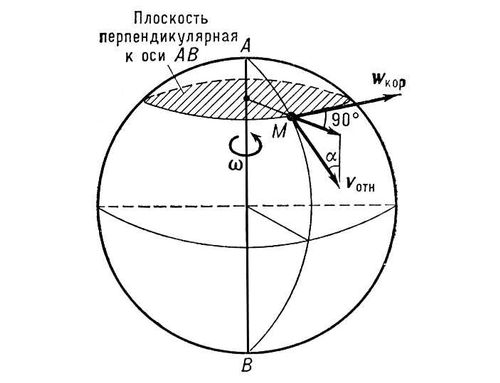 – угловая скорость поворота движения системы отсчета вокруг некоторой оси АВ, – угол между v_r и осью АВ).

Как вектор ускорение Кориолиса определяется формулой

W_C = 2[w_еv_r].

Случаи, когда ускорение Кориолиса равно нулю:

1). Подвижная система координат движется поступательно (w_е=0);

2). V_r = 0;

3). (w_еv_r) – находятся на параллельных прямых.

Ускорение Кориолиса – это часть ускорения точки по отношению к основной, а не к подвижной системе отсчета. Например, при движении вдоль поверхности Земли вследствие ее вращения точка будет иметь ускорение Кориолиса по отношению к звездам, а не к Земле.

Правило Жуковского

Чтобы найти направление ускорения Кориолиса, нужно: вектор относительной скорости спроектировать в плоскость, перпендикулярную w_е и повернуть проекцию на угол 90^о в сторону вращения.