Дәрежелiк функция: голоморфтылығы, бірбеттілік еместігі, бірбеттілік облыстары.

Функция w=zⁿ (1),

n- дәрежелік функция деп аталатын натурал сан.

Функцияның анықталу облысы барлық комплексті жазықтық болалады.

Егер n>1болса, онда дәрежелік функция өзара мәндес болмайды,яғни қайтымды бола алмайды. Егер Муавр формуласы бойынша:

Осыдан шығатыны, кезде (1)-ші теңдік орын алады егер

бүтін болса.

w=z² кескінін толығырақ қарастырсақ. Осы кескіндеуде z аргументтері еселенеді,онда үстіңгі жарты жазықтық UOV –ның барлық жазықтығында өтеді.

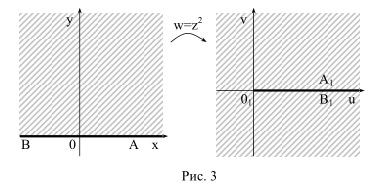
Осы кезде ОА және ОВ сәулелері (3-суретте) UOV жазықтығына OU осьтің оң бағыты бойынша бір сәулеге өтеді. Өзара мәндес сәйкестіктермен жұмыс жасау ыңғайлы ,яғни XOY жазықтығы бар ОА сәулесі осы қиманың O₁A₁ үстіңгі жағасына өтеді,ал ОВ – төменгі жағасына О₁В₁.

Дәл солай төменгі жартылай жазықтық қиылған UOV жазықтығына өтеді,ОВ сәулесі үстіңгі жағаға,ал ОА- төменгіге өтеді. Кескіннің мәндестігін сақтау үшін, осы екі қиылған жазықтықты екі бөлек беттер деп санау оңай. Жағаларды жапсыру керек: ОА бірінші жазықтықтың үстіңгі жағасына және төменгі жаға екінші жазықтығынаөтеді. Дәл солай қиықтың бірінші жазықтығының төменгі жағасын қиықтың екінші жазықтығының төменгі жағасын жапсыру керек – осы екі жағалар бір ОВ сәулесінің кескіні болып табылады.

Алынған екібеттік бетті риман беті деп w=z² функциясы үшін аталады.

Мысал1. АВС үшбұрышымен шектелген облыстың бейнесін табу керек.

А(-1;0); В(0;1), С(1;0) w=z² кескіні кезінде.

Шешуі. w=z²=(x²-y²)+ixy.

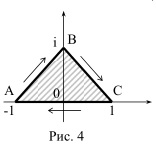облыстың орғыту бағытын таңдаймыз(4-сур). А,В,С, нүктелерінің бейнесін және АВ,ВС,АС түзуін табамыз:

A=(-1;0) →A₁=w(A)=1

B=(0;1) →B₁=w(B)=-1

C=(1;0) →C₁=w(C)=1.

AB: y=1+x. u және v функциялары үшін формуланы алмастырамыз:

Бірінші теңестіруден x табамыз және екінші теңестіруге қоямыз

Дәл солай ВС бейнесін аламыз : y=-x+1; ол парабола болады СА түзуі : y=0 оң OU жарты жазықтығына өтеді.

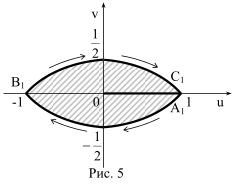
ОС және ОА бір бейнеде болады,осы қиық бойынша оң жарты жазықтықты OU кесіп аламыз. Бейнелерді құрсақ А₁,В₁,С₁. Облыстың орғыту бағытының сақталуы образдың өзінің бейнесін табуға рұқсат береді. (5-сур).

Комплекс сандар логарифмы. Логарифмдік функция. Комплекс санның комплекс дәрежесі.

Комплекс облыстағы логарифмдік функция көрсеткіштік функцияға кері функция ретінде анықталады, яғни, егер болса, онда болады. Егер және десек, онда болады. Осылардан және . Бірінші теңдңктен . Демек,

.

Сонымен, логарифмдік функция барлық және анықталған шексіз көп мәнге ие екендігін көреміз. болғандағы мәні логарифмнің басты мәні деп аталып, арқылы белгіленеді. Яғни, .

Нақты айнымалы комплекс мәнді функцияның кесінді бойынша интегралы. Сызықтық, аддитивтік, қасиеттері, айнымалыны алмастыру.

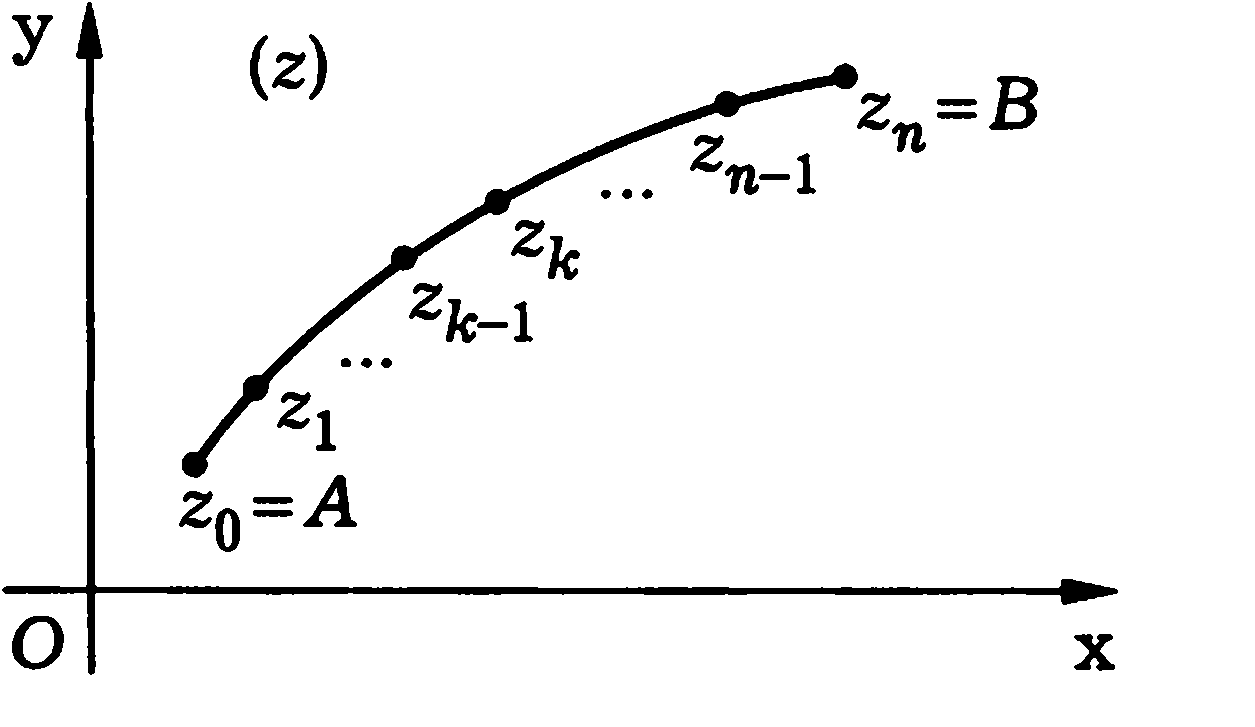z жазықтығында АВ үзік тегіс қисығы берілсін ( А және В сәйкесінше қисықтың бастапқы және соңғы нүктелері).Осы қисықтың әрбір нүктесінде f(z) функциясы анықталсын деп ұйғарайық.АВ қисығын нүктелері болатын доғаларына бөлейік. арқылы ) доғаның ұзындығын белгілейік, максимал ұзындық. Әрбір доғасында нүктесін алып интегралдық суммасын құрайық.

Егер кезде интегралдық суммның соңғы шегі болса,онда бұл шекті функциясының АВ қисығы бойынша алынған интегралы деп атайды және оны осылай белгілейді.Сонымен

АВ-интегралдау жолы.

(5.2) ескере отырып

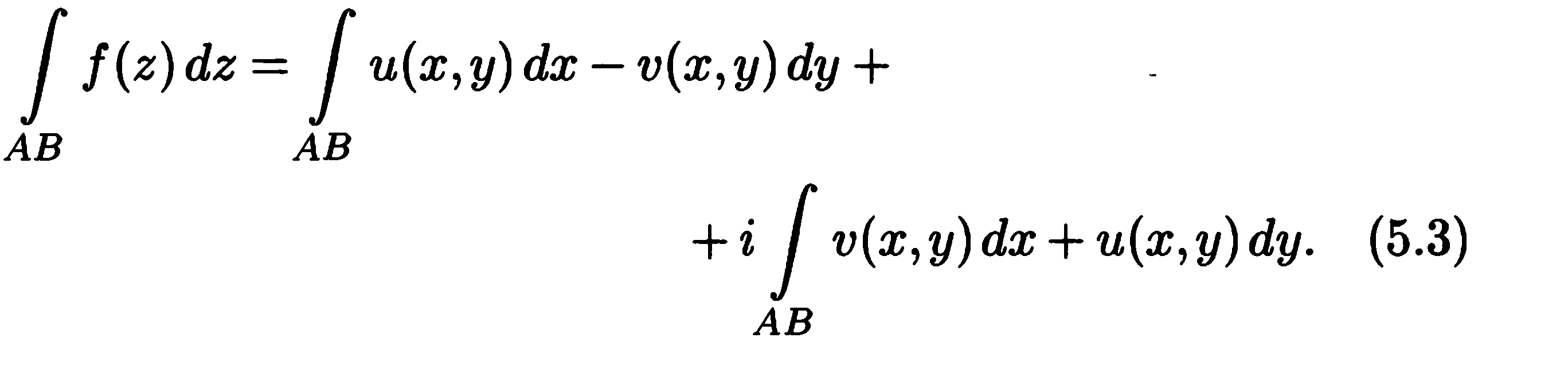
Соынмен комплекс айнымалы функцияның АВ қисығы бойынша алынған интегралы-екі нақты айнымалы комплекс мәнді қисық сызықты интегралдардың болуына парапар.

Сызықтылық

Егер функциялары АВ үзік тегіс қисығында үзіліссіз болса,онда кез келген а және b тұрақтыларына дұрыс.

Аддивтивтілік АВ және ВС үзік тегіс қисықтары берілсін.Кез келген АС үзіліссіз қисығындағы функциясына келес қатынас дұрыс:

Қисықтар, тегіс, үзік-тегіс қисықтар. Комплекс айнымалы функцияны қисық бойынша интегралын екі нақты екінші текті қисық сызықты интегралдар ретінде өрнектеу. Интегралдың қисық бағытына тәуелділік, біртектілік, доға бойынша аддитивтілік, функция бойынша аддитивтілік қасиеттері.

Жол деп фукнциясындағы нақты t аргументінің және әрбір нүктесінде үзіліссіз болатын комплекс – мәнді функциясы.Кез келген үшін аймағы бар , ал t –ның барлық нүктелері үшін болады. a=z(a) және b = z(β) жолдың шегі деп атайды (егер α<β, онда а- басы, ал b аяғы болып есептеледі) Егер осы 2 нүкте тең болса , онда жол тұйық деп аталады. Мына 2 жолды : және эквиваленті дейміз, егер деген өспелі үзіліссіз функциясы барлық нүктелерінде болса. Эквиваленттілікті екенін: рефлексифтілігінен , симметриялығынан

және транзитивтылылығынан білеміз. Енді, қисық деп жолдың эквиваленттілік класстарын айтады.Егер қисық жазықтыққа қатысты үздіксіз өзгерісте болса онда бұл қисық тегіс деп аталады. Ал, егер жазықтықтағы қисық тегіс доғалардың шекті сандарынан тұрса онда, оны үзік –тегіс қисықтар деп атайды.

Эквивалентті жолдардың класстарын ҚИСЫҚТАР деп атаймыз. Жол деп комплекс жазықтығында мынадай: үзіліссіз функцияны атайды. Жолдың комплекс түрде жазылуы:

Мынадай түрде берілген екі жолды эквивалент жолдар деп атаймыз.