Дәрежелік қатардың қосындысының өз жинақталу дөңгелегінде голоморфты болатындығы туралы теорема.

Мына

Түріндегі қатарды комплекс облыстағы дәрежелік қатар деп атайды, мұндағы

Коэффиценттері – мәні тұрақты комплекс сандар , z – тәуелсіз косплекс айнымалы.

(2.6) дәрежелік қатардың жинақты болатны барлық z мәндерінің жиыны осы қатардың жинақталу облысы деп аталады.

Абель теормасы: 1)Егер нүктесінде (2.6) дәрежелік қатары жинақты болса , онда теңсіздігін қанағаттандыратын кез келген z үшін берілген қатар абсолют жинақты болады.

2) Егер нүктесінде (2.6) дәрежелік қатары жинақсыз болса , онда теңсіздігін қанағаттандыратын кез келген z үшін берілген қатар жинақсыз болады.

Анықтама: шамасын (2.6) қатарының жинақталу радиусы деп , ал дөңгелегін (2.6) қатарының жинақталу дөңгелегі деп атайды. дөңгелегін (2.6) қатарының жинақталады , ал осы дөңгелектің сыртында – жинақталмайды. (2.6) дәрежелік қатардың жинақталу радиусы мына формуламен анықталады:

Теорема. Кез келген дәрежелік қатардың суммасы

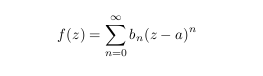
өз жинақталу дөңгелегінде голоморфты болады. F(z) үшін мүшелеп алынған дифференциалдық қатардың туындысының дәрежелік қатарының қосындысы болып табылады.

Дәлелдеу: R арқылы f функциясының жинақтылық радиусын белгілейік және R>0 деп алайық. F(z) үшін мүшелеп алынған дифференциалдық қатарды қарастырайық :

Оның жинақтылық радиусы да R-ге тең , себебі .

Бұл қатар мына теорма бойынша жинақтылығы анықталады. Дәрежелік қатар

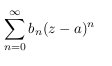
Әрбір үшін жинақталады, сонымен қоса компакті көпшілікте жинақтылық теңеседі. Осы теорема бойынша g теореманың 2 шартын қанағаттандырады, яғни мыналарды:

1. G функциясы 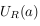үзіліссіз

2. Кез келген үшбұрыш үшін

Алғашқы функцияның бар болуы туралы теорема бойынша

интегралы U – да голоморфты және U – да шартын қанағаттандырады.

G(ξ) үшін [a,z] бойынша мүшелеп интегралдау мынаған тең:

Бұдан f функциямыз U – да голоморфты және дәлелдеуміз бойынша.

Көрсеткіштік функция, оның қасиеттері. Эйлер формулалары. Тригонометриялык функциялар sinz, cosz, tgz, ctgz: барлық қасиеттері дерлік нақты жағдайдан көшіріледі. Бірақ, sinz >1 болуы мүмкін.

Комплекс облыстағы көрсеткіштік функция периодты. Оның периоды . Шынында да, кез келген бүтін n үшін .

Тригонометриялық функциялар. Комплекс облыстағы және функциялары

,

формулалармен, ал және функциялары

и

формулалармен анықталады.

Тригонометриялық функциялар үшін нақты айнымалының тригонометриялық функцияларының көптеген қасиеттері сақталады. және функцияларының периоды , ал және периоды болады.

Нақты нүктелері функциясының нөлдері болатындықтан, осы нүктелерде функциясы анықталмаған. Осы сияқты функциясының нөлдері болатын нүктелерінде функциясы анықталмаған. Барлық тригонометриялық тепе-теңдіктер де сақталады. Бірақ комплекс облыстағы және функциялары шенелмеген.

Гиперболалық функциялар келесі фрмулалармен өрнектеледі:

, , яғни, .