57. Анализ безубыточности производства.

Точка безубыточности — минимальный объём производства и реализации продукции, при котором расходы будут компенсированы доходами, а при производстве и реализации каждой последующей единицы продукции предприятие начинает получать прибыль. Точку безубыточности можно определить в единицах продукции, в денежном выражении или с учётом ожидаемого размера прибыли.

Синонимы: критическая точка, CVP-точка.

Не путать с точкой окупаемости (проекта). Она рассчитывается для определения времени, когда прибыль проекта превысит затраты на него потраченные, это та же точка безубыточности, только измеряется не в штуках, а в месяцах и годах.

Точка безубыточности в денежном выражении — такая минимальная величина дохода, при которой полностью окупаются все издержки (прибыль при этом равна нулю):

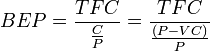, где

BEP (англ. break-even point) — точка безубыточности,

TFC (англ. total fixed costs) — величина постоянных издержек,

VC (англ. unit variable cost) — величина переменных издержек на единицу продукции,

P (англ. unit sale price) — стоимость единицы продукции (реализация),

C (англ. unit contribution margin) — прибыль с единицы продукции без учёта доли переменных издержек (разница между стоимостью продукции (P) и переменными издержками на единицу продукции (VC)).

Можно заметить, что выражение численно равно отношению валовой маржи к выручке.

Точка безубыточности в единицах продукции — такое минимальное количество продукции, при котором доход от реализации этой продукции полностью перекрывает все издержки на её производство:

.

58. Использование системы MathCad для решения уравнений.

Первоначально рассмотрим СЛАУ в Mathcad. Для их решения может использоваться блок given …find( ) или специальная функция lsolve( ). Применение блока given …find( ) предопределяет необходимость задания начальных значений искомых переменных. Далее после ключевого слова given описывается СЛАУ и с помощью find( ) находится решение. Следует указать, что в том случае, когда СЛАУ в Mathcad имеет бесконечное множество решений блок given …find( ) дает конкретный результат, что несомненно следует отнести к недостаткам. В случае отсутствия решения будет выдано сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию”.

Применение функции lsolve( ) позволяет избежать этого недостатка. Функция lsolve(M,b) имеет два аргумента. M – матрица коэффициентов при неизвестных, b – вектор свободных членов. На листинге приведля решения системы нелинейных уравнений используются два блока: given…find( ) и given…minerr ( ). Так как система нелинейных уравнений может иметь несколько решений, то полученные результаты зависят от начальных значений искомых переменных. В обоих случаях получаются приближенные решения, для которых рекомендуется делать проверку. Обычно в Mathcad требуется, чтобы количество уравнений было равно количеству искомых переменных, но в некоторых случаях, когда с точки зрения классической математики может быть получено точное решение и при меньшем количестве уравнений, данное условие может быть нарушено. На листинге представлены примеры использования блоков given…find( ) и given…minerr ( ) для решения систем нелинейных уравнений.ен пример решения СЛАУ.