Питання для самоперевірки:

1. Що таке механічний рух? Що вивчає статика?

2. Що вивчає теоретична механіка? Задачі статики.

3. В чому полягає суть понять матеріальна точка та абсолютно тверде тіло?

4. Що таке сила? Які три характеристики має сила?

5. Що таке система сил?

6. Що таке еквівалентна система сил?

7. Яка сила є рівнодійною системи сил?

8. Як формулюються аксіоми статики?

9. В якому випадку матеріальне тіло буде вільним?

10. Як зображується рівнодійна двох сил, які прикладені до тіла в одній точці?

11. Сформулюйте теорему про три непаралельні сили.

Висновок по темі: При розв'язанні задач слід дотримуватися наступної послідовності:

1. Визначити тіло, рівновагу якого слід розглянути в даній задачі.

2. Показати на рисунку всі активні сили, які діють на вибране тіло.

3. Звільнити від в'язей вибране тіло і замінити їх дію силами реакцій в'язей. Зобразити у вигляді векторів усі сили реакцій відкину­тих в'язей.

4. Скласти рівняння, яке б виражало умови рівноваги тіла. Тип цих рівнянь визначається характером сил, що діють на тіло.

Зокрема, при розв'язуванні задач з теми "Плоска система збіж­них сил" з використанням геометричної умови рівноваги необхідно побудувати замкнутий силовий трикутник. Його побудову необхідно починати з відомої сили, далі за відомими елементами трикутника знайти невідомі величини. Якщо силовий трикутник косокутній, то при розв'язуванні корисно використати теорему синусів, але інколи доцільним є використання умови пропорціональності сторін двох по­дібних трикутників (силового трикутника і трикутника за основним рисунком).

1.2. Теорія моментів сил

Під час вивчення даної теми необхідно ознайомитись з проекцією сили на вісь і на площину, приведенням збіжних сил до рівнодійної і умовою рівноваги системи збіжних сил.

Вивчити теорію моментів сил: момент сили відносно точки, поняття пари сил, момент пари сил.

Опрацювати приклад розв’язання задач з використанням рівнянь рівноваги системи збіжних сил.

Завдання: Балка АВ підтримується в горизонтальному положенні стержнем СD. Закріплення в точках А, С, D – шарнірні.

Визначити реакції шарніра А і стержня СD, якщо на кінці балки діє вертикальна сила = 5кН. Розміри вказані на рис. Вагою балки нехтуємо.

Розв’язання:

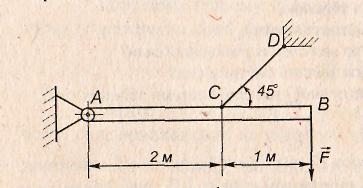
1. Розглянемо рівновагу балки АВ.

2. Показуємо активну силу .

3. Звільняємо балку від в’язей. В’язями є шарнір А і стержень DC. Дію в’язей заміняємо реакціями. Реакція стержня DC направлена вздовж стержня. Напрям реакції шарніра А знаходимо виходячи з умови, що лінії дії сили , реакції шарніра А і стержня DC перетинаються в одній точці.

4. Вибираємо осі координат як вказано на рис.

5. На балку діє плоска система збіжних сил. Складемо рівняння рівноваги:

∑ F_іх = 0; – R_A· cosα + R_c· cos 45^o = 0;

∑ F_іу = 0; – F – R_A· sinα + R_c· sin 45^o = 0.

Звідси:

R_A = F/ cosα – sinα; R_c = F· √2 cosα / cosα – sinα.

Оскільки

sinα = 1/√10; cosα = 3/ /√10,

то

R_A = 7,9 кН, а R_c = 10,6 кН.

Дана тема найкраще висвітлена у навчальному посібнику: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 20 – 36.

Теоретичні відомості

Теорія моментів сил

1. Проекція сили на вісь і площину.

2. Приведення збіжних сил до рівнодійної.

3. Теорія моментів сил.

Література

1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.

2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.

1. Проекція сили на вісь і площину.

Уявимо силу , вектор якої довільно розташований у площині креслення (рис. 1.8). Виберемо у цій площині вісь, наприклад, вісь . Необхідно спроектувати вказану силу на дану вісь .

Рис. 1.8

Позначимо спочатку кінці вектора сили літерами і і опустимо з них на вісь перпендикуляри. Точки перетину перпендикулярів з віссю (позначимо їх відповідними малими буквами і ) утворили на осі напрямлений відрізок, який і буде проекцією сили на вісь . За величиною цей відрізок дорівнює добутку модуля сили на косинус кута, під яким вектор сили перетинає вісь. А саме:

. (1.4)

За знаком проекція сили на вісь тоді буде додатня, коли кут (кут перетину вектора сили або лінії дії сили з віссю) гострий. Цілком зрозуміло, якщо цей кут дорівнює , то проекція сили на вісь дорівнюватиме нулю. Якщо кут буде тупий, то проекція сили на вісь буде мати від'ємний знак.

Таким чином, проекція сили на вісь – це напрямлений відрізок на осі, утворений між перпендикулярами, які опущені з кінців вектора сили на вісь, і який за величиною дорівнює добутку модуля сили на косинус кута між напрямом вектора сили та віссю.

Спроектуємо тепер вектор сили на площину і осі координат.

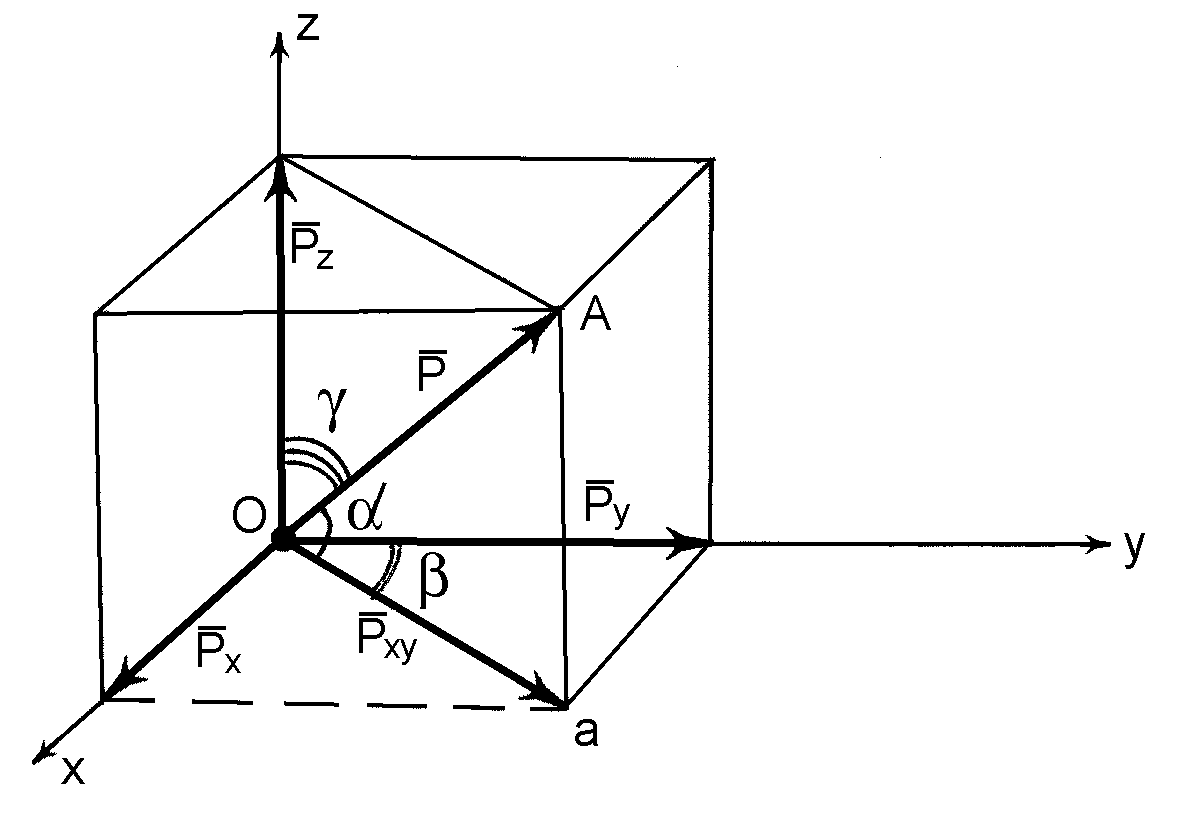
Рис. 1.9

Візьмемо силу , вектор якої довільно розташований у просторі (рис. 1.9). Виберемо у просторі прямокутну декартову систему координат , початок відліку якої (точку ) суміщений з точкою прикладання вектора сили . Спроектуємо вектор сили на площину . Опустимо з точки (кінець вектора сили) на вказану площину перпендикуляр, який перетинає її в точці . На площині утворено вектор , який і є проекцією сили на площину. За модулем ця проекція дорівнюватиме

, (1.5)

де - кут між вектором сили та площиною .

Якщо в площині позначити кут , то є можливість спроектувати силу на осі та , опускаючи з точки на осі перпендикуляри і за відомим вже правилом отримати проекції вектора на вказані осі:

, (1.6)

. (1.7)

У даному випадку крізь вісь та вектор сили можна провести площину, тому є можливість спроектувати силу на цю вісь за відомим правилом. Ця проекція буде дорівнювати

, (1.8)

де - кут між вектором сили та віссю .