Теорема про кінцеве переміщення плоскої фігури

Теорема: фігуру в площині П з одного положення в будь-яке інше можна перевести шляхом одного повороту в цій площині навколо точки Р, яка є центром кінцевого обертання.

Припустимо, що в положенні І фігура характеризується відрізком АВ, незмінно зв’язаним з фігурою, а в положенні ІІ цей відрізок займе положення А₁В₁ (рис. 8).

Припустимо, що точка Р є центром обертання, тобто обертання трикутника АВР до положення ΔА₁В₁Р₁ чиниться навколо точки Р. Оскільки ΔАВР при своєму обертанні не дістає деформації, то ΔАВР = ΔА₁В₁Р₁ та АР = А₁Р, ВР = В₁Р.

Якщо розглядати трикутники АА₁Р та ВВ₁Р, то вони рівнобедрені, оскільки АР = А₁Р, ВР = В₁Р. Крім цього дані трикутники мають спільну вершину – точку Р.

При врахуванні того, що відомі положення І та ІІ відрізка АВ, то відомі (або можуть бути легко знайдені) відрізки АА₁ та ВВ₁. оскільки точка Р є вершиною рівнобедреного трикутника АА₁Р, то вона лежить на перпендикулярі, який проведений з середини відрізка ВВ₁ (тобто з точки D). Якщо врахувати, що точка Р є спільною, то вона лежить на перетині перпендикулярів, які проведені з середин відрізків, що з’єднують початкове та кінцеве положення відповідних точок відрізка АВ фігури.

Рис. 8.

Таким чином, доведена можливість існування та визначене положення центра кінцевого обертання.

Цілком очевидно, що у випадку відсутності перетину цих перпендикулярів (точніше, якщо вони перетинаються в нескінченності), то центра кінцевого обертання немає (або він теж знаходиться у нескінченності). Це буде можливе у тому і тільки у тому випадку, коли відрізки АВ і А₁В₁ паралельні, і лінії, що з’єднують їх відповідні точки, взагалі не перетинаються.

В результаті вивчення теми слухачі повинні

Знати :

• кінематичні рівняння руху;

• швидкості точок тіла при плоско паралельному русі;

• прискорення точок тіла при плоскопаралельному русі.

Вміти:

• визначати прискорення точок тіла при плоскопаралельному русі.

Питання для самоперевірки

1. Який рух називається плоским?

2. Напишіть кінематичні рівняння плоского руху .

3. Чи залежить кутова швидкість плоскої фігури від вибору полюса?

4. Яка існує залежність між швидкістю довільної точки плоскої фігури і швидкістю полюса?

5. В чому полягає теорема про проекції швидкостей двох точок плоскої фігури на лінію, що їх з’єднує?

6. Що називається миттєвим центром швидкостей?

7. В чому полягає теорема про існування миттєвого центру швидкостей?

8. Як визначається положення миттєвого центру швидкостей в різних випадках?

9. Що називається миттєво поступальним рухом?

10. Що необхідно знати для побудови плану швидкостей?

11. Яка існує залежність між прискоренням точки плоскої фігури і прискоренням полюса?

Висновок по темі: Кутова швидкість плоскої фігури визначається діленням швидкостей любої точки цієї фігури на відстань цієї точки до міттевого центру швидкостей.

3. Динаміка

3.1 Динаміка точки

В даній темі при її вивченні необхідно звернути увагу на систему одиниць Розглянути. Диференціальні рівняння руху вільної матеріальної точки

Ознайомитись з основними законами динаміки: законами Ньютона, що покладені в основу динаміки, умовами прямолінійного руху матеріальної точки.

Вивчити першу і другу основні задачі динаміки точки.

Розглянути приклад розв’язання задач динаміки.

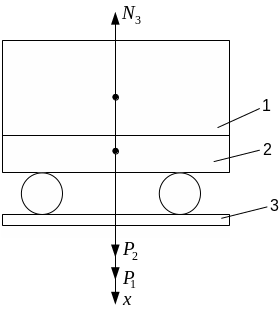
Приклад. Кузов трамвайного вагона разом з вантажем P₁=100 кH здійснює при русі на ресорах вертикальні коливання по закону на візку з колесами (рис. 1). Визначити найбільший і найменший тиск вагона на рейки 3 горизонтального прямолінійного відрізку шляху , якщо візок з колесами важить Р₂ =10кН.

Рис. 1

Розв’язання Розглянемо рух кузова. Рух цей прямолінійний і проходить уздовж осі х. Тому з трьох рівнянь руху використаємо одне, що в даному випадку приймає вигляд де и ‑ відомі з умов приклада ваги кузова і візка з колесами,

‑ реактивна сила з боку в’язів, рейки.

Звідси .

З умови приклада маємо :

‑ закон руху кузова на ресорах.

Тоді ,

‑ проекція прискорення кузова в напрямку осі х

;

.

Звідси ;

.

Відповідь: .

При розгляді даної теми необхідно використовувати посібник: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 217 – 227.

Теоретичні відомості

Динаміка точки

1. Основні закони динаміки.

2. Диференціальні рівняння руху вільної матеріальної точки.

3. Основі задачі динаміки точки.

Література

1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.

2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.

1. Основні закони динаміки.

Динамікою називається розділ теоретичної механіки, в якому визначається механічний рух матеріальної точки, системи матеріальних точок, твердого тіла під дією прикладених до них сил.

Основоположником динаміки є великий італійський вчений Галілей (1564 – 1642). Він вперше ввів у механіку поняття швидкості і прискорення точки при нерівномірному прямолінійному русі і встановив закони падіння тіл у пустоті. Галілей сформулював перший закон динаміки – закон інерції. Почата Галілеєм робота по створенню динаміки була завершена великим англійським вченим І. Ньютоном (1643 – 1727), який формулює основні закони класичної механіки.

Щоб при загальному вивченні динаміки мати можливість відволікатися від впливу розмірів тіл, вводиться поняття матеріальної точки.

Під матеріальною точкою розуміють матеріальне тіло таких малих розмірів, що відмінністю в русі окремих його точок можна знехтувати і положення якого можна визначити координатами його точки.

Введення поняття про матеріальну точку виправдовує проведений в курсах теоретичної механіки поділ динаміки на дві частини: «Динаміка матеріальної точки» і «Динаміка матеріальної системи».

В розділі «Динаміка матеріальної точки», вивчаючі найбільш простий рух тіла, виясняють принципові поняття і закони динаміки.

В розділі «Динаміка матеріальної системи» переходять до вивчення більш складних рухів тіла, а також до вивчення руху системи тіл.

Маса тіла – це величина, яка характеризує інертність тіла.

Інертність – це властивість тіла чинити опір при спробі привести його у стан руху, або змінити швидкість.

Рівномірний і прямолінійний рух точки називається – рухом по інерції.

Перший закон Ньютона (закон інерції)

Будь-яке тіло (точка) перебуває у стані спокою, або рівномірного та прямолінійного руху, поки деяка причина не виведе його з цього стану.

Другий закон Ньютона (основний закон динаміки)

С ила, що діє на матеріальну точку, надає їй прискорення, яке пропорційне величині сили і має направлення сили.

де m – маса матеріальної точки;

а – прискорення матеріальної точки;

F – сила, що діє на точку.

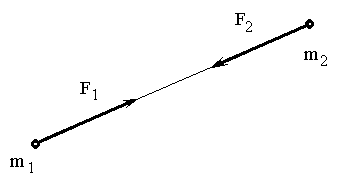
Третій закон Ньютона (закон рівності дії та протидії)

Дії завжди відповідає рівна їй, і протилежно напрямлена протидія, інакше – сили взаємодії двох матеріальних точок завжди між собою рівні і напрямлені в протилежні боки.

Четвертий закон Ньютона (принцип суперпозиції)

При одночасній дії на матеріальну точку декількох сил, прискорення точки складається з тих прискорень, які були б при роздільній дії сил.