Рівняння плоского руху тіла та його точок
Візьмемо у площині руху фігури S систему координат xOy, що є нерухомою по відношенню до цієї площини (рис. 3).
Виберемо за полюс
будь-яку точку
на фігурі і приймемо її за початок
рухомої системи координат
,
незмінно зв’язану з фігурою S.
Положення рухомої системи координат,
як і плоскої фігури S, буде визначатися
положенням точки
і кутом повороту φ по відношенню до
нерухомої осі х.
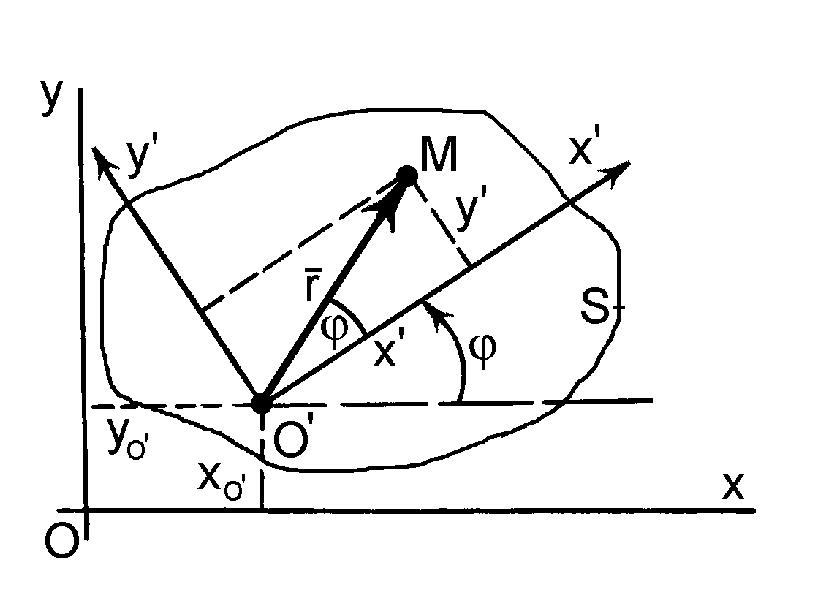
Рис. 3
Протягом часу координати полюса (точки ) і кут φ змінюються і є однозначними функціями часу:
(2.66)
Ці рівняння є рівняннями руху плоскої фігури, або, що одне і те ж, кінематичними рівняннями плоского руху тіла.
2. Швидкості точок тіла при плоско паралельному русі.
Теорема: швидкість будь-якої точки плоскої фігури дорівнює векторній сумі швидкості полюса і обертальної швидкості цієї точки навколо полюса.
Маємо плоску фігуру S, яка здійснює складний рух (рис. 4). Швидкість будь-якої точки цієї фігури, зокрема точки В, можна уявити, як векторну суму переносної та відносної швидкостей:
,
де
- абсолютна швидкість точки В відносно
нерухомої системи координат;
- швидкість точки В у переносному
поступальному русі;
- швидкість точки В у відносному
русі, тобто в обертанні навколо полюса
(наприклад, точки А).
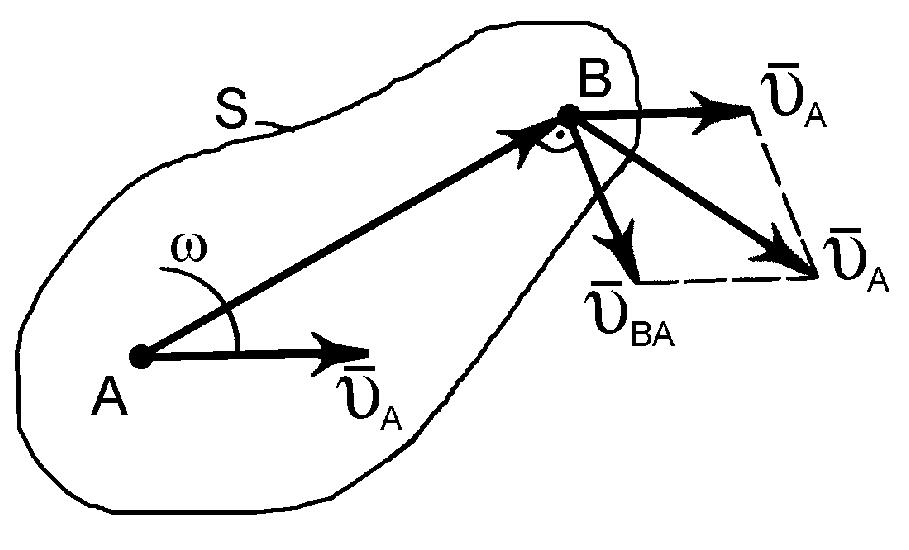
Рис. 4
Оскільки за переносний прийнято поступальний рух фігури S, то переносні швидкості будь-яких точок фігури, зокрема полюса А, однакові, тобто:
.
Величина швидкості у відносному русі, оскільки він є обертальним, дорівнює:
,
де вектор швидкості лежить у площині фігури і спрямований перпендикулярно відрізку АВ у бік обертання фігури S.
Будемо позначати
відносну швидкість
.
Це позначення показує, що точка В у
відносному русі обертається навколо
точки А. Тоді:
.
Теорему доведено.
Наслідок: проекції швидкостей двох точок плоскої фігури на лінію, яка проходить через ці точки, рівні між собою.
Розглянемо точки А і В плоскої фігури, яка здійснює складний рух (рис. 5).
Рис. 5.
Приймемо точку А за полюс, навколо якого обертається у відносному русі точка В.
Згідно тільки що доведеної теореми можна записати
.
Розглянемо проекції
швидкостей
та
на лінію, яка з’єднує обидві точки: 
,
,
але
,
оскільки
.
Отже,
,
тобто
,
або
.
Знаючи модуль
швидкості даної точки
і кут нахилу
вектора цієї швидкості, а також напрямок
вектора шуканої швидкості будь-якої
іншої точки
(кут
),
можна визначити її модуль, тобто
.
3. Миттєвий центр швидкостей і способи його визначення.
Миттєвим центром швидкостей, називається точка Р рухомої плоскої фігури, швидкість якої в даний момент часу дорівнює нулю.
Вказана точка може бути розташованою або на самій рухомій фігурі, або на її уявному продовженні.
Розглянемо фігуру S, яка здійснює плоский рух (рис. 6). швидкість деякої точки А цієї фігури вважається відомою і дорівнює , напрям обертання та кутова швидкість ω обертання фігури теж вважаються відомими і показані на рис. 6.
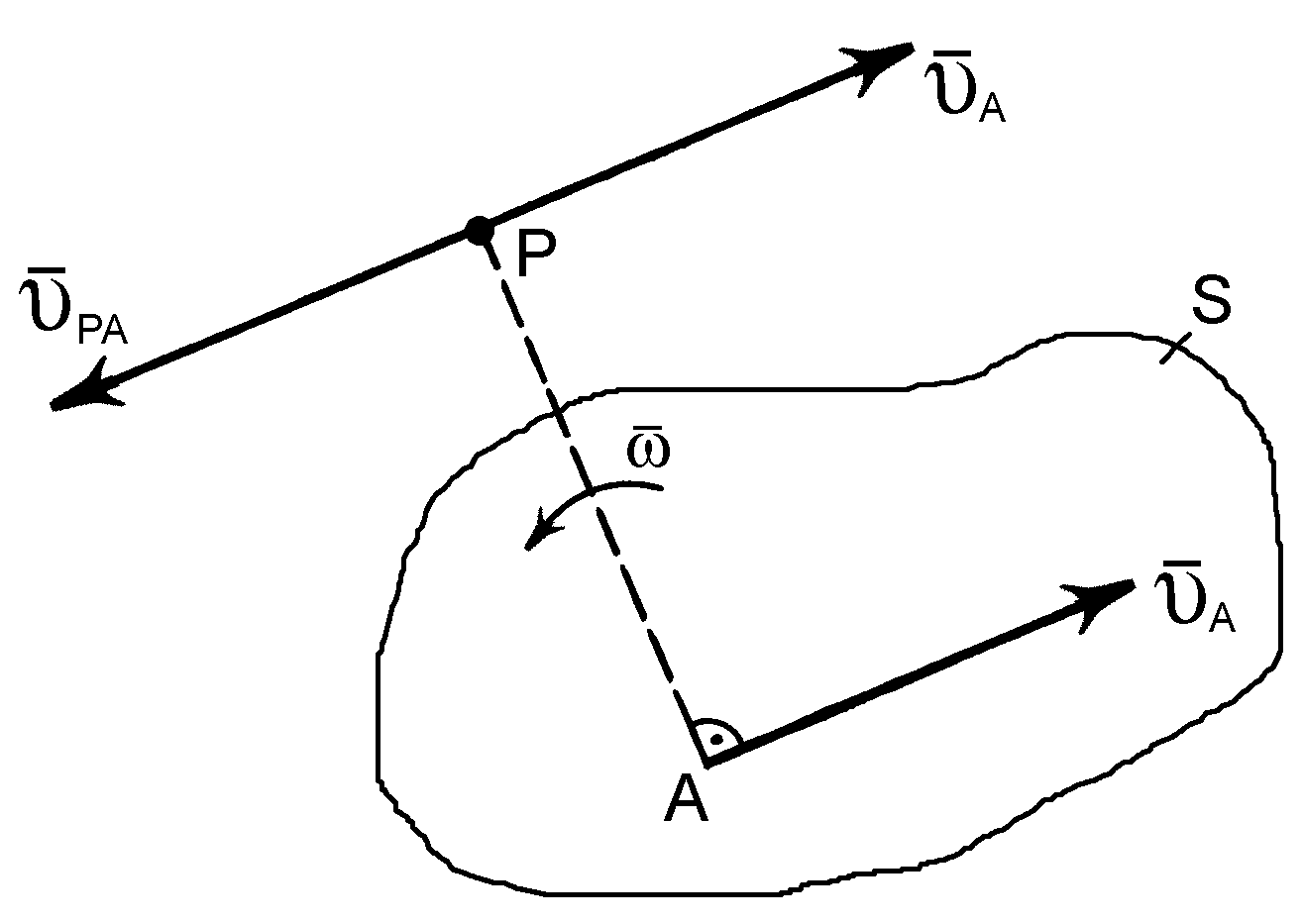
Рис. 6
Зробимо далі таку
побудову: опустимо з точки А
перпендикуляр до вектора швидкості
,
який напрямлений у бік обертання фігури.
Відкладемо на цьому перпендикулярі
відрізок довжиною
.
Приймемо точку А за полюс, тоді
швидкість точки Р даної фігури буде
визначатись за допомогою такого
векторного рівняння:
.
З цього виразу
знайдемо швидкість
.
Вона буде дорівнювати:
.
Вектор швидкості буде напрямлений протилежно вектору швидкості , тобто
.
Тоді, підставляючи це значення швидкості у вираз для швидкості точки Р, остаточно будемо мати:
.
Таким чином,
швидкість точки
дорівнює нулю, і тим самим доведено
існування миттєвого центру швидкостей.
Способи визначення положення миттєвого центру швидкостей
Розглянемо декілька окремих випадків визначення положення миттєвого центру швидкостей. При цьому можуть бути такі випадки (рис. 7):
1. Миттєвий центр швидкостей фігури розташований на перпендикулярі, який проведено до напрямку вектора швидкості деякої точки фігури (рис. 7, а).
2. Миттєвий центр швидкостей фігури може бути знайдено як точку перетину двох перпендикулярів, які поставлені з двох точок фігури до напрямків векторів швидкостей цих точок (рис. 7, б).
3. Якщо вектори швидкостей двох точок фігури паралельні (рис. 7, в), а самі точки не лежать на одному перпендикулярі до напрямків їх швидкостей, то обертання в цей момент відсутнє, і фігура здійснює в даний момент поступальний рух, а швидкості усіх точок фігури дорівнюють одна одній.
.
Додамо, що в цьому випадку, на відміну від поступального руху, прискорення точок будуть різні.
4. Якщо вектори швидкостей двох точок фігури паралельні (рис. 7, г), точки лежать на одному перпендикулярі до напрямків їх швидкостей, а модулі швидкостей не однакові, то миттєвий центр швидкостей міститься у точці перетину прямої, що з’єднує кінці векторів швидкостей з вказаним вище перпендикуляром.
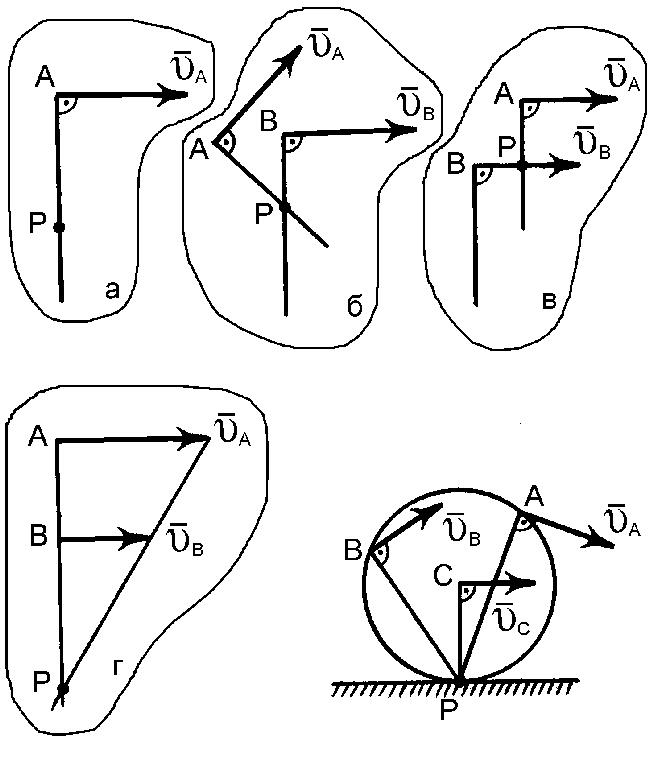
Рис. 7
Тоді, як бачимо з (рис. 7, г), матимемо:
.
5. При коченні фігури без ковзання по деякій нерухомій кривій миттєвим центром швидкостей буде точка дотику фігури з цією нерухомою кривою (рис. 7, д).
6. Кутова швидкість фігури в кожний даний момент часу дорівнює відношенню модуля швидкості будь-якої точки фігури до відстані від цієї точки до миттєвого центру швидкостей.