Питання для самоперевірки

1. Що називається абсолютно твердим тілом?

2. Назвіть основні види руху твердого тіла.

3. Який рух твердого тіла називають поступальним і які він має властивості?

4. Чи можуть точки тіла при поступальному русі описувати довільні траєкторії?

5. Який рух твердого тіла називають обертальним навколо нерухомої осі?

6. Сформулюйте теорему про поступальний рух.

7. Що називають кутом повороту?

8. Що називають середньою кутовою швидкістю? миттєвою кутовою швидкістю?

9. За якими формулами визначають модуль кутової швидкості?

10. Як напрямлений вектор кутової швидкості?

11. Що називають середнім кутовим прискоренням? миттєвим кутовим прискоренням?

12. За якими формулами визначають модуль кутового прискорення?

13. Як напрямлений вектор кутового прискорення?

Висновок по темі: При розв'язанні задач на обертання твердого тіла навколо не­рухомої осі часто буває доцільним додатне направлення осі обертання вибрати таким чином, щоб ω_z була додатною величиною. В цьому випадку ε_z > 0 якщо обертання тіла прискорене і ε_z < 0, якщо обе­ртання сповільнене. Тоді замість ω_z можна взяти ω, а замість ε_z можна взяти + ε або - ε_z.

2.3. Плоскопаралельний рух твердого тіла

Під час вивчення даної теми необхідно ознайомитись з кінематичними рівняння руху.

Вивчити кінематичні характеристики швидкість і прискорення точок тіла при плоско паралельному русі.

Розглянути миттєвий центр швидкостей і способи його визначення.

Опрацювати приклад розв’язання задач з визначення швидкостей точок в плоскопаралельному русі.

Завдання:

У механізмі соломотряса (рис. 2.33) кривошип АВ обертається зі сталим числом обертів n = 225 [об/хв.] Визначити кутові швидкості коромисла C₁D і шатуна B₁C₁ тоді, коли кривошип АВ₁ і шатун В₁С₁ утворюють одну пряму, якщо АВ₁ = 50 [мм], В₁С₁ = 1250 [мм], C₁D = 250 [мм], S = 1250 [мм], h = 100 [мм].

Розв'язування.

Визначимо спочатку положення миттєвого центра швидкостей шатуна за допомогою відомих напрямів швидкостей двох точок В₁ і С₁. Вектор швидкості точки В₁ спрямований перпендикулярно до кривошипа АВ₁, вектор швидкості точки С₁ – перпендикулярно до коромисла DC₁. Миттєвий центр швидкостей шатуна розташований на перетині перпендикулярів, опущених з точок В₁ і С₁ до векторів їх швидкостей. Ці перпендикуляри перетинаються в точці С₁, яка і є миттєвим центром швидкостей шатуна В₁С₁. Тоді швидкість точки С₁ у даний момент дорівнює нулю. Оскільки коромисло DC₁ має дві нерухомі точки, то кутова швидкість його дорівнює нулю. Кутову швидкість шатуна В₁С₁ визначимо за формулою:

.

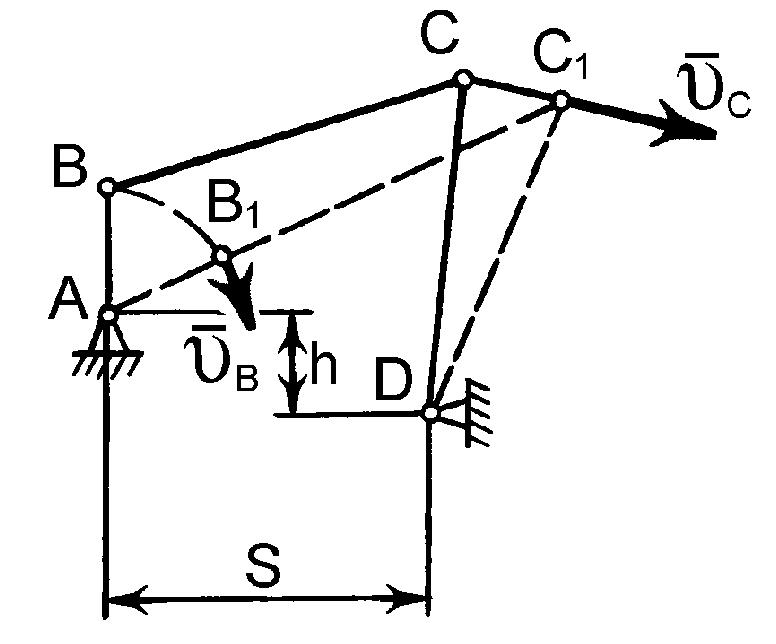
Рис. 1

Швидкість точки В₁, яка водночас є кінцевою точкою кривошипа АВ, можна визначити за допомогою кутової швидкості кривошипа:

, [м/с].

Отже

, [ ].

Дана тема найкраще висвітлена у навчальному посібнику: В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003. Стор 158 – 171.

Теоретичні відомості

Плоскопаралельний рух твердого тіла

1. Кінематичні рівняння руху.

2. Швидкості точок тіла при плоско паралельному русі.

3. Миттєвий центр швидкостей і способи його визначення.

Література

1. В.В. Цасюк Теоретична механіка. –Львів: Афіша, 2003.

2. Е.М. Нікітін Теоретична механіка. – М: Наука, 1983.

1. Кінематичні рівняння руху.

Плоским або плоско паралельним називається такий рух твердого тіла, при якому всі точки тіла рухаються у площинах, паралельних деякій заданій нерухомій площині.

На рис. 1. призма при русі займає послідовно три положення.

Перехід із положення І у положення ІІ призма здійснює у поступальному русі, перехід у положення ІІІ – у плоскому русі, оскільки, наприклад, пряма АВ переходить у пряму , які є непаралельними.

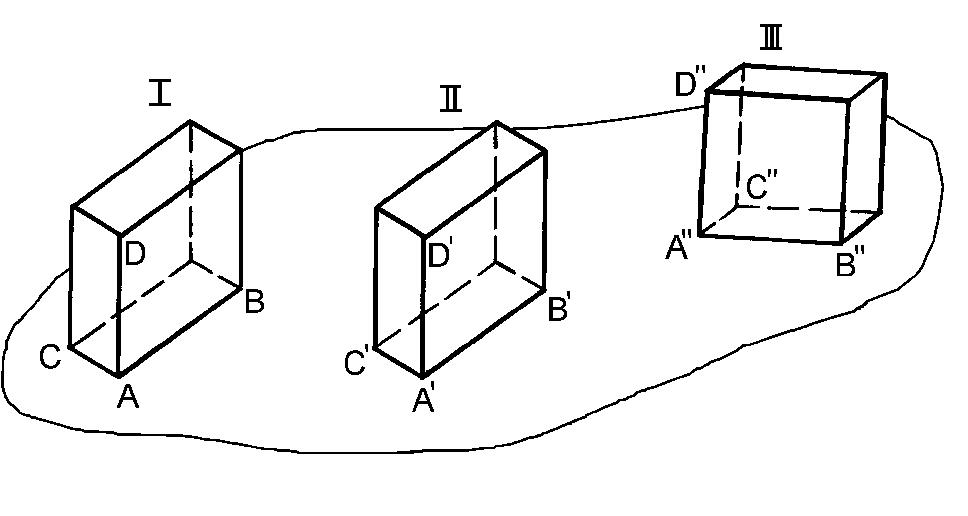
Рис. 1

Розглянемо тверде тіло, яке здійснює плоский рух, паралельний деякій нерухомій площині П (рис. 2.).

Рис. 2.

Якщо ми перетнемо тіло площиною Oxy, яка паралельна нерухомій площині П, тоді у перерізі дістанемо плоску фігуру S. При русі тіла ця фігура буде переміщуватися, залишаючись весь час у площині Oxy. Очевидно, що при плоскому русі всі точки перпендикуляра до площини фігури рухаються однаково, як і точка “а”, маючи однакові швидкості і прискорення, тому що цей перпендикуляр рухається поступально. Якщо взяти на перерізі другу точку “b” і провести перпендикуляр , то всі його точки будуть мати однакові швидкості і прискорення, але і . Якщо на перерізі взяти будь-яку кількість точок, то можна охопити все тіло разом. Таким чином, рух перерізу S може повністю репрезентувати плоско паралельний рух всього тіла.

Звідсіль випливає, що для визначення плоского руху тіла достатньо знати рух плоскої фігури S, одержаної перерізом тіла площиною, яка паралельна даній нерухомій площині.