1.2. Описание переходных процессов в нагрузках

Нагрузки узлов электроэнергетических систем при исследовании устойчивости могут учитываться различными способами в зависимости от поставленной задачи и от требуемой точности её решения. При этом вся комплексная нагрузка какого-либо узла или её части могут замещаться эк­вивалентным синхронным или асинхронным двигателем, учитываться ди­намическими характеристиками или постоянным сопротивлением.

1. Описание переходных процессов в синхронных двигателях

Наиболее точным описанием переходных процессов в синхронном двигателе, как и для генератора, являются уравнения Парка-Fорева.

U

М

Рис. 1.13. Положительное направление тока и моменты, приложенные к ротору двигателя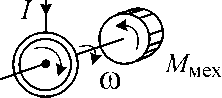

Учитывая, что двигатель в отличие от генератора потребляет электри­ческую энергию и момент, развиваемый двигателем, является вращающим моментом (рис. 1.13), уравнения для двигателя записывают в виде систе­мы (1.53)-(1.56):

• уравнения напряжений обмоток двигателя

djq

(1.53)

^dyVj

c/\|/

(Ь54)

— - - i r •

^{— l}D ' D ’

dt d\\i

r ■

dt

^lQ^rQ’

уравнения потокосцеплений обмоток двигателя

(1.55)

Vd ~ ^xd ^ld ^xad ¹ f ^xad ^lD ' q ~ ^Xq ^lq ^{+ x}aq ’

V/ ^{= x}ad ^ld ^{+ x}f^lf ^{+ x}fD ^lD ’

Vz> ^{= X}ad ^ld ^{+ X}fD ^lf ^{+ X}D^lD’

У О ~ ^Xaq lq ^X0 *О ’

уравнение движения ротора двигателя

(1.56)

В общем случае момент сопротивления механизма, присоединённого к ротору двигателя М_мех, зависит от скорости вращения. Можно принять

(1.57)

М,

мех

— М _сх + (Af о — М _ст)ш“,

где М_ст-момент сопротивления механизма при скорости со = 0 (стати­ческий момент); М₀ - момент сопротивления механизма при номинальной скорости вращения со₀; а - коэффициент, обычно равный 0 н- 2.

Полные уравнения Парка-Горева для описания переходных процессов в синхронных двигателях при исследовании устойчивости электрических систем применяются редко. Обычно используются упрощённые уравнения. Упрощение уравнений Парка-Горева для синхронного двигателя осу­ществляется точно так же, как и для синхронного генератора. При этом, как и для синхронного генератора, для синхронного двигателя имеется не­сколько математических моделей, характеризующихся различной степе­нью точности описания переходных процессов.

2. Описание переходных процессов в асинхронных двигателях

При анализе переходных процессов больших ЭЭС уравнения Парка- Горева для асинхронных двигателей обычно записываются либо в проек­циях на систему координат, вращающуюся со скоростью со ₀, либо в про­екциях на систему координат, ось q которой совмещена с вектором напряжения узла сети, к которому подключен двигатель. В последнем слу­чае в расчёте появляется много систем координат, вращающихся с различ­ными скоростями со_ш, и возникает необходимость многократных пересче­тов параметров режима из одной системы координат в другую. Здесь для асинхронного двигателя будет использоваться система координат, враща­ющаяся со скоростью со ₀. Обычно это общая система координат для ЭЭС

в целом.

Учитывая симметрию асинхронных двигателей по продольной и по­перечной осям, уравнения двигателя можно представить так:

dw_p

(1.58)

мех ’

M = Im(W).

Здесь обозначено

4' = y_q + jy_d;

U = u_q+ju_d;

*c ~ ~ ⁵

= Vo + j'Vd ;

¹ = ^lq + j^ld ’

Xp X^> X^ ₅

^p Iq j h > ■>

■^ц ^{— x}ad ~ ^xaq ’

со*, со о*- скорость вращения ротора двигателя и координатной систе-

Для описания момента механизма, присоединённого к асинхронному двигателю, можно использовать (1.57).

Модель асинхронного двигателя, не учитывающая электромагнитную инерцию обмоток статора. В уравнениях (1.58) следует положить г = О, d^¥/dt = 0. Учитывая, что в относительных единицах

d® ds

dt dt’

(Dq = 1; со₀ — со = .s';

получим

мех

-M;

7 M_]

at

(1.59)

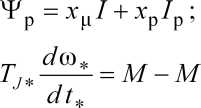
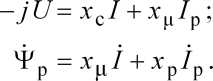
Из двух последних уравнений выразим токи обмоток двигателя:

(-ус/)

t^d = -j—'й- 2 Р ^

7 =

х"х

X

F

Хц у

0 — Р

v_p -*ц

х_сх_р-х_ц

(1.60)

^=7-

h =

+

2 Р х_сх_р - Х_ц

X X

X х_г

^ЛС^Л Р - ^Лц

Введём обозначения:

(1.61)

х = х_с -

£' = j-K.Y •

р "^vp С учетом этих обозначений первое уравнение (1.60) получает вид за­кона Ома:

U = E" + jx"i. (1.62)

Подставляя ток 7_р из (1.60) во второе уравнение (1.59) и учитывая

(1.61), получим в итоге

„ ds

(1.63)

dt

- + je>₀s \Ё",

dE" х„ - х" •

С7-

dt х_с Т"

где

_r ^ХР х" _т Х^ ® 0 ^гр ^хс ^Р *с

М = ту® о* = [E"_qU_d -E"_du_q)/x".

Таким образом, при принятых допущениях асинхронный двигатель в схеме замещения системы должен быть представлен ветвью с сопротивле­нием х" и ЭДС Ё" (рис. 1.14).

Рис. 1.14. Замещение асинхронного двигателя ЭДС Е"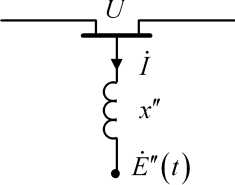

Изменение Ё" в переходном режиме описывается системой уравне­ний (1.63).

Модели асинхронного двигателя, не учитывающие переходные элек­тромагнитные процессы. Дальнейшее упрощение уравнений, описываю­щих переходные процессы в асинхронном двигателе, связано с неучётом переходных электромагнитных процессов и в обмотках ротора. Во втором уравнении системы уравнений (1.63) для этого следует положить dE"/dt = 0. Объединив это уравнение с (1.62), после преобразований по­лучим:

U = ZI:

+ jx

J^xi

ар

(1.64)

Z = jx_a+-

⁺ J'(^xap ^+хц)

где х_а, х_ор - сопротивления рассеяния обмоток статора и ротора.

Эквивалентное сопротивление двигателя Z соответствует схеме за­мещения, приведённой на рис. 1.15, которая получила название Т- образной.

*ар

/т.

/т

U

^rv/s

Рис. 1.15. Т-образная схема замещения асинхронного двигателя

Таким образом, при принятых допущениях в общей схеме замещения электрической системы асинхронный двигатель должен быть представлен Т-образной схемой, а из уравнений, описывающих переходные процессы в двигателе, осталось только уравнение движения ротора:

T, — = M„_PV -M:

ds_

dt

(1.65)

M = P/&_0tt = Re(u²/zy

Определять активную мощность, потребляемую двигателем, по Т- образной схеме замещения достаточно сложно. Так как сопротивление взаимоиндукции х_и значительно больше сопротивления рассеяния обмот-

г¹

Р

ки статора х_а, то х ставят перед х_а и приходят к Г-образной схеме за­мещения асинхронного двигателя, приведённой на рис. 1.16. Такая схема может быть использована при моделировании всей «асинхронной» нагруз­ки узла электрической сети.

х

_TYYV

U

х„

^rp/s

Рис. 1.16. Г-образная схема замещения асинхронного двигателя

(1.66)

В приведённой схеме х = х_с+х_ор. Активная мощность, потребляе­мая двигателем, необходимая для (1.65), в соответствии с приведённой схемой замещения определяется выражением:

Р =

r_D² + (s х)²

В переходных режимах ЭЭС напряжения в узлах сети, к которым под­ключены асинхронные двигатели, могут изменяться значительно. При этом значительно будут изменяться и скольжения роторов двигателей. Сопро­тивления двигателя х_ц, х, г_р зависят от величины напряжения на обмот­ках статора и скольжения ротора л_д по отношению к вектору напряжения статора, 5_Д = s-s_v. Изменение индуктивных сопротивлений двигателя объясняется изменением степени насыщения стали. Активное сопротивле­

ние обмотки ротора г_р зависит от частоты наводимого тока в обмотке ро­тора. Частота тока зависит от скольжения .у_д . Чем больше частота, тем больше г_р из-за вытеснения тока к поверхности проводников обмотки ро­тора.

Для Г-образной схемы замещения двигателя изменение хприбли­жённо можно учесть так

= W

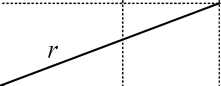
Можно принять к^= 2. При организации расчётов переходных режи­мов нужна именно - проводимость ветви намагничивания в схеме за­мещения двигателя. Зависимости х(я_д) и г_р(5_д) представлены на рис. 1.17 в виде кусочно-линейных аппроксимаций [1].

X,

Гл

р

Рис. 1.17. Зависимости х(з_д) и Гр(5_д)

Расчётные схемы ЭЭС для анализа переходных режимов, как правило, включают только сети 220 кВ и выше (основная сеть ЭЭС) и насчитывают многие сотни и даже тысячи узлов. В качестве нагрузок в такой схеме фи­гурируют потоки мощности, уходящие с подстанций основной сети в сети более низкого напряжения, в основном в сети 110 кВ, и далее к множеству конечных потребителей. Поэтому обычно возникает необходимость моде­

лировать не один какой-то двигатель (с его рабочим механизмом), а боль­шую группу двигателей, одним эквивалентным, подключенным, например, к шинам 110 кВ основной сети. В [1] приведены следующие параметры эк­вивалентного асинхронного двигателя для моделирования нагрузок основ­ной сети, о. е. : cosф = 0,8; М_тах=1,7; М_п=0,73; /_п = 4,1; £_ном=2%; .s_р =70%; к^= 4; £₃=0,7; М_СТ = 0,5; Г_у=0,8с-для

кратковременных возмущений; Tj = 0,6 с - если двигатели глубоко тор­мозятся.

Этим данным соответствуют следующие параметры Г-образной схе­мы замещения двигателя: х₀ =0,368; х₁ =0,266; г₀ =0,0226;

rj =0,0424; х_(Д=2,95.

В целом моделирование асинхронной нагрузки (60-70 % потребления в узле) выполнить точно невозможно. Однако требования к точности мо­делирования высоки. Ведь расчёты переходных режимов ЭЭС осуществ­ляются с целью обеспечения эффективного противоаварийного управле­ния.

3. Учёт переходных процессов в комплексных нагрузках с использованием их статических характеристик

Нагрузка в схеме замещения системы представляется ветвью (рис. 1.18) с некоторым сопротивлением х_н* = 0,2 ^-0,4 , за которым приложена ЭДС Е, изменяющаяся во времени.

U и

Рис. 1.18. Представление комплексной нагрузки в переходном режиме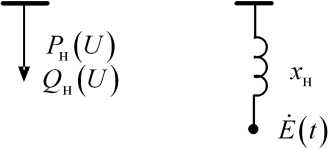

При этом переходные процессы в комплексной нагрузке приближённо учитываются так:

T„- = U-jx„^--E, ^н dt ^{J н} U

где S_H = Р_н(U) + jQ_H(U) - мощность нагрузки, учитываемая статическими характеристиками; Т_и - постоянная времени, выбираемая из опыта расчё­тов.

При необходимости можно учесть и зависимость мощности, потреб­ляемой комплексной нагрузкой от частоты:

'P_B(U,s) = (l + k_Ps)P_a(U);

Q_n(U,s) = (\-k_Qs)Q_n(U),

дР дО

где к_Р = ——, к₀ = - составляющие регулирующего эффекта

ds ds

нагрузки по частоте; s - скольжение вектора напряжения на шинах нагрузки по отношению к системе координат, вращающейся со скоростью

4. Учёт нагрузки постоянным сопротивлением

При исследовании устойчивости электроэнергетических систем нагрузки узлов могут замещаться постоянными сопротивлениями, опреде­ляемыми по параметрам исходного установившегося режима:

z .-"L

Н I £

/

При этом уменьшается общее количество дифференциальных уравне­ний, описывающих переходные процессы в системе. Это оправдано для удаленных от места возмущения нагрузок, а также для нагрузок малой мощности.