3. Представление процесса на фазовой плоскости

Для качественного анализа может оказаться полезным рассмотрение зависимости относительной скорости ротора от угла Асо (8) (рис. 5.8). При этом плоскость координат Асо и 8 называется фазовой плоскостью.

В рассматриваемом случае при отсутствии рассеяния энергии колеба­ний характеристика Асо (8) имеет вид замкнутой кривой, а характер про­цесса во времени 8(t) представляет собой незатухающие колебания.

В действительности имеет место рассеяние энергии колебаний, и ха­рактеристика Асо (8) будет иметь форму спирали, скручивающейся к точ­ке, отвечающей новому установившемуся режиму, а процесс во времени - затухающие колебания.

Рис. 5.8. Фазовая и временная переходные характеристики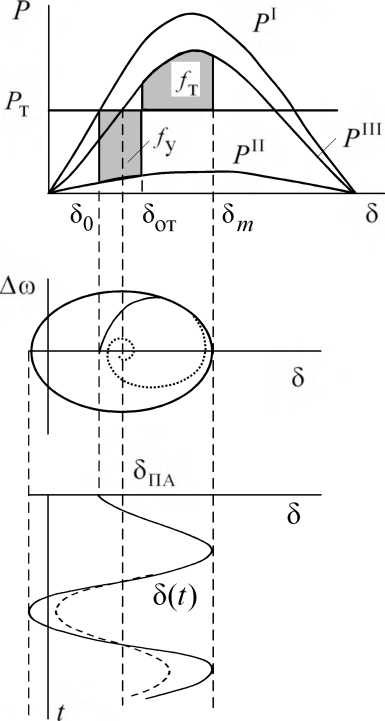

3. Динамическая устойчивость сложной электроэнергетической системы

Расчёты динамической устойчивости выполняются либо на стадии проектирования развития той или иной части ЭЭС, либо на стадии эксплу­атации ЭЭС. В первом случае расчёты устойчивости выполняются про­ектными организациями с целью выбора наилучшего варианта развития ЭЭС, обладающего требуемым запасом устойчивости. При этом одновре­менно выбираются и средства противоаварийной автоматики. Границ энергопредприятий, как правило, не придерживаются. Схема берётся тако­го размера, который позволит правильно решить все вопросы. Во втором случае расчёты устойчивости выполняются системным оператором. При этом расчётные схемы составляются для операционных зон каждого ОДУ с присоединением специально рассчитанных эквивалентов соседних регио­нов. Целью выполнения расчётов устойчивости здесь является настройка существующей противоаварийной автоматики для обеспечения устойчиво­сти ЭЭС.

В расчётную схему входят обычно все источники рассматриваемого региона и сети напряжением, как правило, 220 кВ и выше с их нагрузками. Расчётная схема может насчитывать до 3000 узлов и более.

Рассмотрим электроэнергетическую систему, схема замещения кото­рой содержит N узлов. При составлении математического описания пе­реходных процессов в ней для простоты будем считать, что все генераторы (генерирующие блоки) одной станции в расчёте могут быть представлены одним эквивалентным генерирующим блоком. Разобьём все узлы схемы замещения электроэнергетической системы на четыре группы:

1. узлы, близкие к местам приложения возмущающих воздействий, имеющие генерирующие блоки;

2. узлы, достаточно удалённые от мест приложения возмущающих воздействий, имеющие генерирующие блоки;

3. узлы, близкие к местам приложения возмущающих воздействий, имеющие нагрузки;

4. остальные узлы.

Для генерирующих блоков в узлах группы 1) необходимо взять более точные математические модели, учесть действие регуляторов возбуждения и скорости. Поэтому в качестве моделей элементов одного генерирующего блока возьмём уравнения (1.42) - (1.45), (1.72) - (1.78), (1.81) - (1.82).

Для генерирующих блоков в узлах группы 2) возьмём более простые математические модели. Генераторы будем учитывать с помощью (1.52). Действием регуляторов возбуждения и скорости пренебрегаем, считая Е' = const, Р_Т = const.

Нагрузку каждого узла группы 3) разобьём на две части: «двигатель­ную» и статическую. Первую будем моделировать уравнениями (1.63) с учётом (1.61), (1.62). Вторую представим постоянной проводимостью

Нагрузку каждого узла группы 4), если она есть, представим посто­янной проводимостью.

Электрическую сеть в общей модели ЭЭС представим уравнениями узловых напряжений. При этом могут учитываться все активные и реак­тивные сопротивления и проводимости на землю элементов сети и факти­ческие коэффициенты трансформаций. С учётом принятых моделей гене­рирующих блоков и нагрузок узлов уравнения узловых напряжений будут выглядеть так:

	%1		Щ
	Уе2	.	Е\	(5.4)
			Ё з
	0		0

Здесь все матрицы блочные. Размерность блоков определяется числом узлов в соответствующей группе узлов. Первая строка относится к группе узлов 1), вторая - к группе узлов 2) и т. д. Блочные матрицы Y_ek - диа­гональные. Диагональными элементами этих матриц являются проводимо­сти ветвей, которыми представлены соответствующие генераторы или дви­гатели в схеме замещения системы. Собственные проводимости узлов Yц

должны включать в себя проводимости ветвей с ЭДС Y_ej и проводимости

ветвей нагрузок Y_Hi, если соответствующие ветви подключены к узлу i.

Будем считать, что параметры моделей генерирующих блоков в узлах группы 1) в расчёте будут представлены в относительных номинальных единицах соответствующих блоков, а параметры схемы и режима всех остальных элементов системы - в именованных единицах. (Можно было бы принять и другое решение.)

Примем, что все векторные параметры режима элементов сети (напряжения и токи) будут определены в системе координат (q_c, d_c) угло­вую скорость которой выберем равной со₀, соответствующей частоте 50

Гц. Принятые модели генераторов в узлах группы 2) и модели двигателей определены именно в такой системе координат. Что касается генераторов, подключенных к узлам группы 1), то принятые для них модели определе­ны в системе координат их собственных роторов, которые могут вращаться в переходных режимах с различными скоростями. В связи с этим в расчё­тах необходимо производить пересчёт некоторых параметров режима ге­нераторов в узлах группы 1) из системы координат (с/, с/) их роторов в

систему координат (q_c, d_c) и обратно. В рассматриваемом случае пере­считывать необходимо только напряжения и ЭДС генераторов:

(«,/+>л) ^{= С>}(/®'^; d = {E"_q!+jE’d,)h> (5.5)

где Q; — Uj _ном ■ с .

Следует помнить, что в принятых моделях в уравнения движения ро­торов моменты необходимо подставлять в относительных номинальных единицах.

В целом составленная система уравнений, описывающая переходные процессы в сложной ЭЭС, будет подобна (1.86), (1.87).

Для определения параметров установившегося режима, в котором необходимо проверить устойчивость ЭЭС, вначале рассчитывается режим работы электрической сети при заданных, например, узловых потоках мощности и напряжении в базисном узле. Затем, зная напряжения всех уз­лов сети, определяются параметры режима всех генерирующих блоков и нагрузок. Для этого следует использовать принятые для описания пере­ходных процессов в них уравнения, положив все производные по времени равными 0. Следует использовать также соотношения (5.5).

Задав возмущающее и управляющие воздействия, определяются начальные условия интегрирования. При этом все параметры режима х,

входящие под знак дифференцирования, являются инерционными коорди­натами и в первый момент времени остаются неизменными. Остальные па­раметры режима у - определяются через них путем решения системы ал­гебраических уравнений, входящей в (1.86).

Численное интегрирование системы уравнений (1.86), описывающей переходные процессы, часто осуществляется методом Рунге-Кутта четвер­того порядка. Расчёт параметров режима на очередном к-м шаге интегри­рования продолжительностью At производится в следующей последова­тельности.

1. 5 = 0.

^xi(k) ~ ^xi(k-\)> i — ■>

Xj — Xj{j, i -\,п ,

У j ⁼ У _j(k-\)’ j = lm.

2. s := s +1.

Axi =F_i(x_l,...,x_n,y_l,...,y_m)At, i = 1,n ;

^xi(k) •'= ^xUk) + ^a,v - i = ^l’K.

3. Если s = 4, то перейти к п. 4.

^xi = ^xi(k-\) + fis^Axi > i = ln.

Определить yj,j = \,m, решив систему уравнений

ф_](х₁,...,х_п,у₁,...,у_т) = 0, j = I,т.

Перейти к п. 2.

4. Определить yj_(k),j = \,m из системы уравнений

^Фj {х\(к)’--->^хп(к)’У\(к)’---’Ут(к)) = °- J = ^l’^m-

Здесь а и Р ■ массивы коэффициентов:

а = [1/6, 2/6, 2/6, 1/6], р = [1/2, 1/2, 1].

Так как расчёт одного шага в методе Рунге-Кутта состоит из четырёх

вспомогательных шагов (s = 1,4) , то на одном шаге четыре раза необхо­димо решать систему алгебраических уравнений из (1.86), которая в ос­новном состоит из уравнений узловых напряжений (5.4).

Величина шага интегрирования At зависит от наименьшей постоян­ной времени из всех элементов системы и может составлять 0,01-^ 0,001 с. Для того чтобы вынести заключение об устойчивости системы, необходи­мо увидеть, как будут изменяться взаимные углы роторов генераторов 5ij (7) в течение 3 ^ 5 с. Из этого следует, что трудоемкость процесса чис­ленного интегрирования очень высока. Затраты времени на численное ин­тегрирование составляют основное время расчётов динамической устойчи­вости.

Контрольные вопросы

1. Динамическая устойчивость ЭЭС. Этапы анализа динамической устойчивости и их характеристика.

2. Формирование математической модели ЭЭС для исследования динамической устойчивости.

3. Определение начальных условий.

4. Что такое возмущающие и управляющие воздействия?

5. Как осуществляется наблюдение за переходным режимом ЭЭС?

6. По каким параметрам можно сделать заключение о динамической устойчиво­сти большой ЭЭС?

7. Энергетические соотношения, характеризующие движение ротора генератора, работающего в простейшей системе. Метод площадей.