3. Энергетические соотношения, характеризующие движение ротора генератора. Способ площадей

Для простейшей электроэнергетической системы (см. рис. 5.1) при описании переходных процессов в ней уравнениями (5.1) характер относи­тельного движения ротора эквивалентного генератора станции после от­ключения КЗ можно установить, рассматривая энергетические соотноше­ния сил, действующих на ротор.

Определив проводимости схемы у_п, у₁₂ для нормального, аварийно­го и послеаварийного режимов, можно построить характеристики мощно­сти эквивалентного генератора станции для этих режимов:

(рис 5.7).

Нормальный режим будет соответствовать точке 0, в которой уравно­вешены электромагнитная мощность генератора и мощность турбины. В первый момент КЗ угол 8 (инерционная координата) скачком измениться не может, 8^ = 8₀, и поэтому новый режим будет отвечать точке 1 на

характеристике мощности Р^и режима КЗ. Так как теперь генератор будет

отдавать меньшую мощность, чем он получает от турбины, то под дей­ствием избыточного момента ДМ* = AR, = P_T,_f - R, ротор генератора начнёт ускоряться.

рШ

5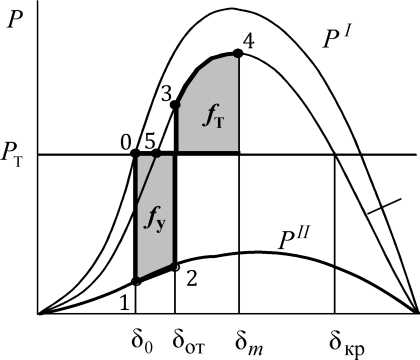

Относительные перемещения ротора отражаются уравнением движе-

j, dА© _ др

^J dt

Учитывая, что

dAa> JAco db _А dA&

= = А© ,

dt db dt db уравнение движения можно записать так:

Tj • A© -dAcd = АР ■ db.

Интегрируя это уравнение, найдём кинетическую энергию, получен­ную ротором при его ускорении:

1. ^от

Ay = — Tj • А©² = J(P_T-Pⁿ(5))-d5.

2. s₀

Кинетическая энергия, приобретённая ротором в процессе ускорения численно равна заштрихованной на графике площадке /_у, которая полу­чила название площадки ускорения.

После отключения КЗ генератор будет отдавать в сеть мощность большую, чем он получает от турбины (точка 3 на характеристике после- аварийного режима Р^и]). Ротор начнёт тормозиться, теряя приобретён­ную им кинетическую энергию и скорость. Энергия торможения будет равна:

.

A_t=-Tj-A(o² = |(р^ш(5)-/>_т)-б/5.

² 8от

Она представлена на рис. 5.7 площадкой торможения /_т

В точке 4 относительная скорость ротора А© становится равной 0. Но так как генератор будет по-прежнему отдавать большую мощность, чем он получает от турбины, то в следующий момент его относительная ско­рость станет меньше 0, и угол 5 начнёт уменьшаться.

Так как принятое математическое описание переходных процессов соответствует позиционной системе, то рассеяния энергии колебаний (из­быточной энергии) не будет происходить, и поэтому энергии ускорения и торможения в этом случае будут равны, А_у = А_т. Равны будут и площад­ки ускорения и торможения.

Максимально возможная площадка торможения /_тв в рассматривае­мом случае будет ограничена верхней частью характеристики мощности послеаварийного режима Р^1П и характеристикой мощности турбины от 8_0т до 8 _кр. Очевидно, что если /_тв > /_у , то электроэнергетическая си­стема устойчива. Чем больше /_тв по сравнению с /_у, тем больше запас динамической устойчивости.