2. Определение критических напряжений узлов методом утяжеления режима

Для определения критического напряжения U_Kp узла нагрузки сложной

электроэнергетической системы можно воспользоваться критерием устой- d AQ

чивости

< 0 (см. п.2.6.3). Определение зависимости реактивной

dU

мощности Q_c, поступающей из сети в узел при изменении напряжения уз­

ла, можно осуществить методом утяжеления режима по напряжению узла.

Вначале должен быть рассчитан исследуемый на устойчивость режим электрической сети и определены (дорассчитаны) ЭДС источников с уче­том имеющихся у них систем регулирования возбуждения. Модули и фа­зовые углы ЭДС в дальнейшем расчёте остаются неизменными. Далее приступают к определению U_Kp тех узлов, устойчивость нагрузки которых

нужно проверить.

Пусть для определения критического напряжения выбран узел к. Си­стема уравнений, описывающая состояние (режим) электроэнергетической системы, в рассматриваемых условиях будет выглядеть так:

Xf_tjEjU_t+jrf_tjUjU_t + S„_i(U_i) = 0; / = ri + \/N; Ык;

7=1 j>n

N

(4.2)

Re

'L^Y»^E)U_k+'ZY_VU_jU_k

7=1 7>»

U_k=U_k(i).

Решая эту систему уравнений при заданной величине модуля напря­жения узла U^ij, определим напряжения узлов и по ним реактивную

мощность, поступающую из сети в узел к :

Qck = “^Im

I_IAjEjU_k + f_ir_t}UjU_t

7=1 j>ⁿ

Расчёты следует повторить для ряда постепенно снижаемых уровней напряжения узла U_kn\ (0.95?7^₀, 0.9U_kQ,В результате можно по­строить зависимость (рис. 4.3)

m(U_k) = Q_ek(U_k)-Q_xt(U_k), определить критическое напряжение узла и запас устойчивости.

Рис. 4.3. Зависимость \Q/_{(U/_{) и критическое напряжение узла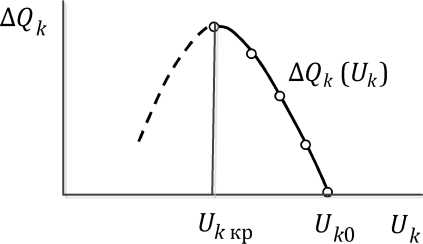

Обследованию подлежат, прежде всего, узлы с большим потреблени­ем и к тому же электрически удаленные от источников.

3. Анализ статической устойчивости электроэнергетической системы путём преобразования схемы

   1. Преобразование схемы к звездообразному виду

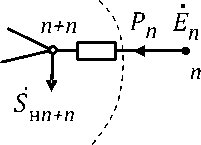Пусть имеется схема сложной электроэнергетической системы (рис.

4. . Для этой системы был рассчитан некоторый плановый (исследуемый) режим. Параметры этого режима ниже отмечаются дополнительным ин­дексом 0. При расчёте режима были определены также ЭДС всех источни­ков E_i0 = E_i()Zb_j0 с учётом АРВ.

Сечение 1 Сечение 2

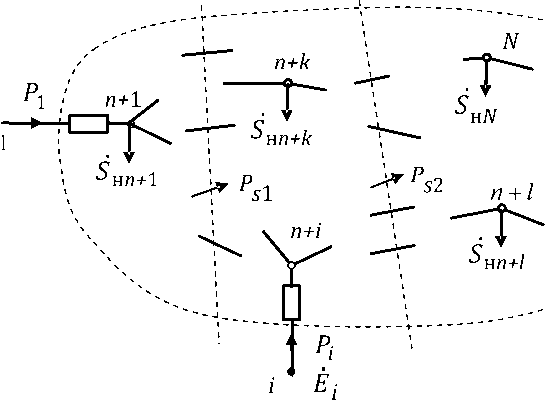
Заменим нагрузки узлов ветвями с постоянными проводимостями Y j = *° = const.

U?o

Зависимость мощности, потребляемой Y_Hi, от напряжения

будет отличаться от фактической зависимости Р_ш (£/_г ), Q_H(U_}) (рис.

4.5). Тем самым вносится определённая погрешность в определении кри­тических напряжений узлов, а также пределов передаваемой мощности ме­тодами, основанными на преобразовании схемы.

Рис. 4.5. Фактические P_Hj, О_н / и приближенные P_Hl, 0_Hj зависимости мощности нагрузки от напряжения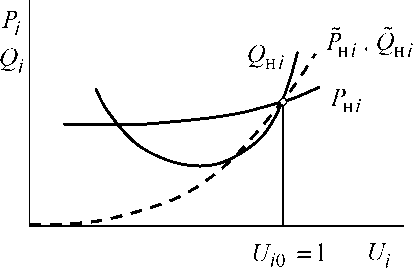

Пусть вначале были пронумерованы узлы с ЭДС (1 , а затем

прочие узлы схемы (п +1, Тогда с учетом того, что ЭДС известны,

(4.3)

систему уравнений узловых напряжений, описывающую установившееся состояние ЭЭС, можно записать так:

V 77+1,77+1	‘ ‘ ^n+l.N	~ип+;		^и+1Д	■ ■ Y 77 + 1, 77	~v
^N,n+\	^ NN	uN _			Ynn	1 : s 1

Собственные элементы Y_H, i = n + l, N, должны включать в себя проводимости нагрузочных ветвей.

Для системы уравнений (4.3) выполним прямой ход метода Гаусса, исключая напряжения узлов от (и+1) до (N-1) включительно. В результате уравнение для узла N примет вид:

П

7=1

где Y_nn,Y_nj - изменённые в процессе исключения элементы матрицы Y.

Запишем это уравнение в виде:

Ут U„ + Y„_nU_n = f/'jEj . (4.4)

Здесь Y*_N = Y_nn -Y_hN, Y^j - проводимости ветвей преобразованной схе-

Уравнение (4.4), представляющее собою баланс токов в узле N, можно представить в форме баланса мощностей:

-Y‘_NU¹_N+U_Nf₄YSjE_j=S_XN. (4.5)

7=1

Из этого уравнения следует, что в результате исключения напряжений из системы уравнений (4.3) (узлов из исходной схемы замещения систе­мы), мы пришли к эквивалентной схеме, представленной на рис. 4.6.

Рис. 4.6. Звездообразная модель электроэнергетической системы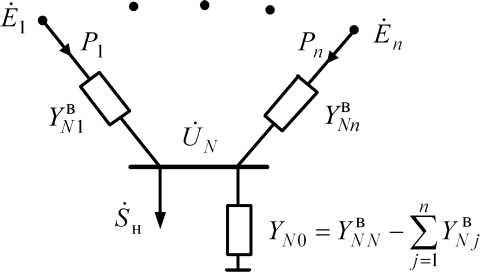

Эта схема называется звездообразной моделью электроэнергетической системы с центром в узле N. Очевидно, что звездообразные модели мож­но получить для всех узлов исходной схемы. Звездообразные модели поз­

воляют достаточно просто определять критические напряжения централь­ных узлов, а также пределы передаваемой мощности генераторов или групп генераторов.

2. Определение пределов передаваемой мощности

Для определения предела передаваемой мощности группы генерато­ров (находящихся по одну сторону от сечения, в частности одного) схему звезды представим в виде рис. 4.7.

Рис. 4.7. Расчётная схема для определения пределов передаваемой мощности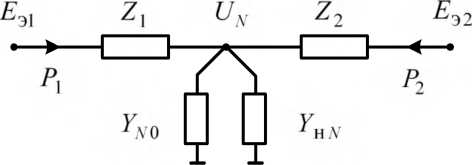

J^&rk

Т В . Nj ’

Здесь

При этом Г_х - множество генераторов, отнесенных к первой группе; Г₂ - остальные генераторы системы.

Характеристика мощности

Р\ = ^ЕЭХ JnSinan + E_3lE₃₂y_l2sin(b_u -a_l2)

и предел передаваемой мощности первой группы генераторов

Здесь

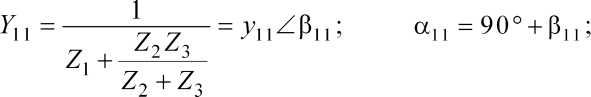
Y12 — у у — У\2^-§\г\ ^ai2^_90° + p₁₂,

Z_t+Z₂+- ^{1 2}

7 ¹

где Z₃ = .

У 4- V ¹ ON ^^JHN

Аналогично определяется предел передаваемой мощности для второй группы генераторов.

2. Определение критического напряжения центрального узла Запишем уравнение (4.5) в виде

^_^эn^n ⁺ УэмU_nE_3N ⁼ S_rN ’ (4-6)

п Л ^п

Y - У 7^В. • К - - У У^в Е

¹эы - Z-I NJ ^, Э N~_v Lu¹Nj^Cu i •

7=0 ^r3N 7=1

В результате придем к расчётной схеме (рис. 4.8)

£, Д> Qu> u_N

] У

i',*

^нЛ'

^HV

кр

Рис. 4.8. Расчётная схема для определения U

dE

Теперь для определения U_KD можно использовать критерии > 0

^F dU

или d-AQ~ < о _{см пп} 2.6.2, 2.6.3.

dU

Контрольные вопросы

1. Определение пределов передаваемой мощности методом утяжеления режима. Общая характеристика метода.

2. Способы утяжеления режима при определении пределов передаваемой мощ­ности.