2. Анализ статической устойчивости простейшей нерегулируемой электроэнергетической системы методом малых колебаний

Рассмотрим подробнее этапы анализа статической устойчивости ме­тодом малых колебаний на примере простейшей электроэнергетической системы, схема которой приведена на рис. 3.3.

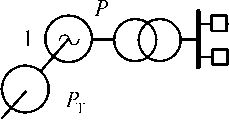
Рис. 3.3. Схема простейшей системы

При составлении математического описания переходных процессов в рассматриваемой электроэнергетической системе в качестве описания переходных процессов в турбогенераторах станции возьмем уравнения (1.49). Примем, что М* = P_f. Не будем учитывать переходные процессы в системах регулирования возбуждения и скорости. Не учитываем также электромагнитную инерцию и активные сопротивления элементов сети. Состояние электрической сети при этом будем учитывать уравнениями уз­ловых напряжений. Собственные и взаимные проводимости схемы опре­делим в соответствии с п. 2.4. Тогда с учетом выражений

P = E_qU_cy_nsin8;

id =~Ql^Eq = ~^Е_ЧУп + ^UC У\2 ^{C0S 5}>'

^Eq^=E'q-(^Xd-^X'd)id

при принятых допущениях получается следующее описание переходных процессов в рассматриваемой электроэнергетической системе:

(3.6)

P = P_lmsin8-P_2msin2b ; Р_Т = P₀ = const;

^Eq=^EqO=^nst.

0,5(x_d-x'_d)y²_nU,

Р =

1 т

Р

Здесь

^l-(^xd~^xd)yii ’ ’^2/И !“(*</-*^11 Величины Р₀, являются параметрами исследуемого на устойчи­вость режима электроэнергетической системы.

Выберем в качестве переменной, определяющей состояние электро­энергетической системы в рассматриваемых условиях, угол 8. Осуще­ствим линеаризацию нелинейной зависимости Р(5) путем разложения её в ряд Тэйлора с точностью до линейного члена ряда:

dP

(3.7)

А5.

d 5

Р*Р_{0 +}

Это означает, что фактическая нелинейная зависимость Р(5) в окрестности исходного положения равновесия 5₀ заменена касатель­ной, наклон которой определяется величиной производной

dP

= P_Xmcosb-2P_2mcos2b,

db

вычисленной при 5 = 5₀ (рис. 3.4).

Рис. 3.4. Линеаризация Р(о)

Подставляя выражение мощности (3.7) и угла 5 = 5₀ + А5 в первое

уравнение (3.6), получим линейное (линеаризованное) дифференциаль­ное уравнение:

(3.8)

А5 = 0.

d 5

о

Т_Т d Д5 dP

со₀ dt^z

То же в операторной форме:

Tj 2 1 s dP

— p

AS +

d 8

AS = 0.

CO

0

о

Характеристическое уравнение:

= 0.

Tj ₂ dP

— p

+

<iS

CO

о

Корни характеристического уравнения:

P 1,2

В рассматриваемом случае корни могут быть либо чисто мнимые, ли- бо чисто действительные.

dP

+	со0	dP
1	' Tj	db	0

Мнимые корни появляются при условии

>0.

db

(3.9)

= ±jv.

Р\,2 = ±Л

Tj db

Решением линейного дифференциального уравнения (3.8) будет функция

AS(f) = C_xe^Plt + C₂e^Pl1 = C_xe^jvt + С₂ё

p₂t

,-jvt

При начальных условиях A5₍₀₎ = A8₀; —

d t

0, получим

(0)

A8(7) = A8₀ cos vt.

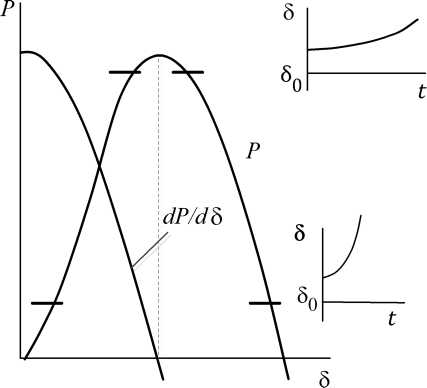
Изменение угла будет происходить в виде незатухающих гармониче­ских колебаний около 8₀ с частотою v (рис. 3.5).

dP

Действительные корни будут, если

<0.

db

При этом

^юо dP Tj db

= +

= ±a.

Pi, 2

Решением уравнения (3.8) при тех же начальных условиях будет A5(f) = С, e^ar + С₂ e~^at = ^{e^at + e~^at).

Изменение угла б будет носить апериодический характер (рис. 3.6).

Рис. 3.6 Изменение угла в случае действительных корней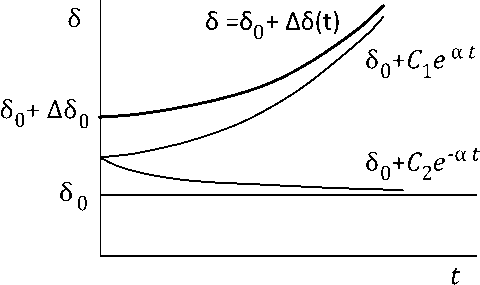

Так как при t —> оо и 5—»оо, то электроэнергетическая система не­устойчива. Неограниченное увеличение угла б, следовательно, и не­устойчивость системы, вызваны наличием положительного действительно­го корня у характеристического уравнения.

Из выражения (3.9) видно, что частота колебаний v будет тем боль­ше, чем больше dP/db. При подходе к пределу статической устойчивости частота колебаний будет уменьшаться, стремясь к нулю (рис. 3.7). В об-

^f dP

<0

изменение угла б будет носить

db

ласти неустойчивых режимов уже апериодический характер.

Рис. 3.7. Характер изменения угла 5

Вблизи предела статической устойчивости изменение угла будет очень медленным. Такой характер нарушения устойчивости называют ино­гда сползанием.

Контрольные вопросы

1. Метод малых колебаний. Последовательность анализа устойчивости методом малых колебаний.

2. Получение линеаризованной системы уравнений в стандартной форме, опи­сывающей переходный режим ЭЭС при малых возмущениях.

3. Характеристический определитель, характеристический полином, характери­стическое уравнение.

4. Каковы должны быть корни характеристического уравнения, чтобы ЭЭС была устойчивой?

5. Перечислите возможные методы анализа корней характеристического урав­нения.

6. Критерий Гурвица.

7. Метод D-разбиения.

2. РЕЖИМЫ, ПРЕДЕЛЬНЫЕ ПО СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ

Практику интересует не только проверка статической устойчивости одного какого-то режима, но главным образом определение предельных по статической устойчивости значений параметров режима при направленном изменении режима. Обычно выяснению подлежат предельные значения активных мощностей Pj_m, которые можно передавать в установившихся

режимах из одной части системы в другую через определенные сечения (пределы передаваемых мощностей сечений), а также критические уровни напряжений узлов U_iKp, ниже которых двигатели, входящие в состав ком­плексных нагрузок этих узлов, остановятся.

В рабочем режиме поток мощности Pj ₀ через каждое сечение схемы

должен быть меньше соответствующего предельного значения на некото­рую величину, а напряжение каждого нагрузочного узла U_i0 должно быть

больше соответствующего критического уровня. Коэффициенты запаса статической устойчивости по мощности k_pj для каждого сечения и по

напряжению к_ш для каждого нагрузочного узла должны быть не менее

соответствующих нормативных значений:

100 ^к_и н₀р_М-

. Oi±m>k

PJ р

jm

Для нормальных режимов к_{р норм} = 20 %, к_{и норм} =15%.

Определение указанных выше предельных параметров осуществляет­ся либо методом утяжеления режима (более точный), либо методом преоб­разования схемы.

1. Определение пределов передаваемой мощности

методом утяжеления режима

Для определения предела передаваемой мощности выбранного сече­ния задается некоторый начальный режим электроэнергетической систе-

мы, в котором переток мощности по выбранному сечению не самый тяже­лый, и рассчитываются все параметры этого режима. Проверяется устой­чивость расчитанного режима. Если режим устойчив, то задается, рассчи­тывается и проверяется на устойчивость следующий режим с несколько большей величиной потока активной мощности через выбранное сечение от генераторов передающей части системы (утяжеленный режим). Шаги утяжеления режима ведут до тех пор, пока с определенной точностью не приблизятся к пределу передаваемой мощности - к границе, которая отде­ляет устойчивые режимы от неустойчивых. Точно определить предел пе­редаваемой мощности сечения невозможно, так как процесс решения си­стемы уравнений установившегося режима вблизи предела передаваемой мощности расходится.

Задание и расчёт режима электроэнергетической системы проще начинать с задания и расчёта режима электрической сети, а затем опреде­лить параметры режима генерирующего оборудования и нагрузок. Смотри, например, рис. 4.Е Электрическая сеть на рисунке обведена пунктирной линией.

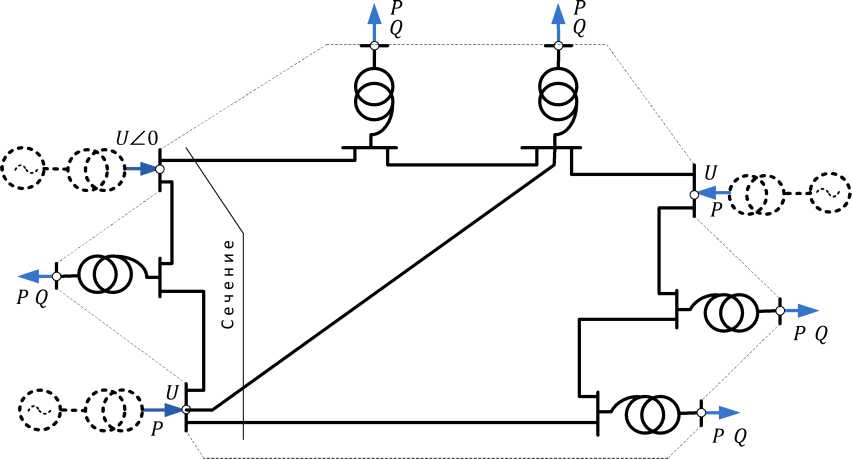
Задание режима электрической сети в рассматриваемых условиях бу­дет состоять в задании модуля и угла напряжения UZ0 в одном из узлов с подключённой генерацией (базисный и балансирующий узел), в осталь­ных узлах с подключённой генерацией в задании Р и U, в нагрузочных уз­лах -Р и Q.

Для расчёта режима электрической сети необходимо составить систе­му уравнений узловых напряжений для всех узлов сети кроме балансиру­ющего. Решить составленную систему уравнений относительно напряже­ний узлов при заданных параметрах режима. По найденным напряжениям узлов определить токи и потоки мощности по ветвям схемы сети.

Параметры режима генерирующего оборудования и нагрузок опреде­ляются, используя найденные параметры режима сети и соотношения, вы­текающие из (1.86) для установившегося режима (все производные по вре­мени в (1.86) нужно положить равными 0).

Утяжеление режима, т.е. увеличение передаваемой мощности через рассматриваемое сечение, может быть осуществлено:

• путем увеличения мощностей нагрузок в некоторой группе узлов при­емной части системы с одновременным увеличением генерируемой мощ­ности определенной группы генераторов в передающей части;

• путем уменьшения генерируемой мощности некоторой группой гене­раторов приемной части системы с одновременным увеличением генери­руемой мощности некоторой группой генераторов передающей части (пе­рераспределение генерации);

• путем утяжеления по углу. Постепенно синфазно увеличиваются фазо­вые углы определенной группы ЭДС передающей части системы так, что­бы загружалось по активной мощности выбранное сечение.

Устойчивость режима на каждом шаге утяжеления может проверяться различным образом: по корням характеристического уравнения; по знаку

свободного члена характеристического уравнения; по знаку якобиана, по критерию dP/d8 > 0.

Определение предела передаваемой мощности с контролем корней характеристического уравнения. На каждом шаге утяжеления после рас­чёта режима необходимо составлять линеаризованную систему уравнений (3.1), определять матрицу А системы уравнений (3.2). Вычислять соб­ственные числа матрицы А. Если все собственные числа будут иметь только отрицательные вещественные части, то расчитанный режим устой­чив. Этот путь наиболее точный, но очень трудоемкий.

Определение предела передаваемой мощности с контролем знака свободного члена характеристического уравнения. В этом случае поиск пределов передаваемой мощности основывается на том, что уже устранены причины возникновения самораскачивания путём соответствующей настройки систем регулирования возбуждения и скорости и причины са­мовозбуждения - наличие достаточно больших емкостных токов в генера­торах и двигателях. В таком случае возможно только апериодическое (не колебательное) нарушение статической устойчивости. Это произойдет при появлении у характеристического уравнения после очередного шага утя­желения положительного вещественного корня, чему будет соответство­вать изменение знака а_п - свободного члена характеристического уравне­ния. Этот путь предполагает: составление линеаризованной системы урав­нений (3.1), определение матрицы А системы уравнений (3.2) и затем определение свободного члена характеристического уравнения а_п=\А\.

То есть на контроль устойчивости требуется большое число арифметиче­ских операций.

Определение предела передаваемой мощности с контролем знака якобиана. Было предложено при рассчёте установившихся режимов на шагах утяжеления идеализировать регуляторы возбуждения, считать, что они поддерживают Е_х = const в некоторых точках схемы (см. п.2.3). Заод­но считается постоянной и частота в системе. Уравнения узловых напря­жений должны быть составлены в форме мощностей. В одном из генери­рующих узлов должны быть заданы Е_х и 5. В остальных генерирующих

узлах -Р и Е_х , в нагрузочных узлах - Р и Q или P(U), Q(U). Составлен­ная в этих условиях система уравнений узловых напряжений будет иметь якобиан, совпадающий по знаку с а_п системы линеаризованных диффе­ренциальных уравнений, не учитывающей электромагнитные переходные процессы в ЭЭС. Следовательно, для неустойчивых режимов якобиан бу­дет неположительным. Если решать такую систему уравнений методом Ньютона, то для неустойчивых режимов итеративный процесс будет рас­ходящимся. Таким образом, предельным по статической устойчивости бу­дет режим, который удалось рассчитать последним в процессе утяжеления. Этот подход сейчас распространен в отечественной практике.

Определение предела передаваемой мощности с контролем устой­чивости по критерию dP/dS >0. Это может применяться, если выбран способ утяжеления режима по углу.

Предел передаваемой мощности в рассматриваемом направлении пе­редачи для выбранного сечения определяется путем серии расчётов уста­новившихся режимов при постепенном увеличении фазовых углов ЭДС генераторов передающей части системы 5_г-/&) •'= ⁺ ^(k) > ^где ^(k)' ^па_

раметр утяжеления. При этом фазовые углы ЭДС генераторов приемной части системы и модули всех ЭДС системы сохраняются равными их зна­чениям в исходном режиме.

Пусть L_x и Ь₂ - множества узлов передающей и приёмной частей си­стемы, содержащих ЭДС, L₃ - множество остальных узлов системы (не

содержат ЭДС). Тогда установившееся состояние электроэнергетической системы можно описать следующей системой уравнений:

' £ f,jU_jU_i+'£ i_ljEjU_i + S_Hl(U_i) = 0;

7. ^E ^ з J

i e £3 / U ^2^

так как ЭДС полностью известны:

S/o + ^А5а)’ j^^Lv Ej = Ejo ⁵,o> j ^&L₂.

£/=£,0

Решив систему уравнений (4.1) при конкретной величине параметра утяжеления режима А 5^, определим напряжения узлов, а затем потоки

мощности ветвей, проходящих через выбранное сечение и суммарный по­ток мощности сечения. Повторяя расчёты при различных значениях АЪ_(к),

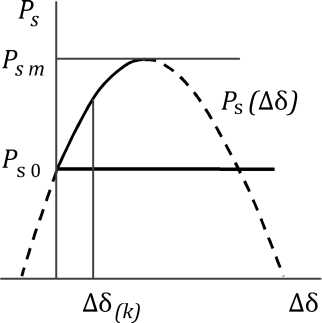
можно построить зависимость суммарного потока мощности P_s контро­лируемого сечения от параметра утяжеления А5 (рис. 4.2) и определить предел передаваемой мощности сечения P_sm .

Рис. 4.2. Характеристика мощности и предел передаваемой мощности сечения