2. Вычисление коэффициентов характеристического уравнения

Существует несколько методов вычисления коэффициентов а₁ харак­теристического полинома. Все они очень трудоемкие и численно неустой­чивые. При больших п (несколько сот, тем более тысяч) практически не­возможно получить а, с хорошей точностью, необходимой потому, что

корни алгебраического уравнения очень чувствительны к его коэффициен­там. В результате заключение об устойчивости может оказаться неверным. Ошибки при вычислении a_i «набегают» при выполнении многочисленных арифметических операций из-за округлений, вызванных ограниченной длиной разрядной сетки ЭВМ.

Объем вычислений при определении коэффициентов характеристиче­ского полинома, исходя из характеристического определителя, соизмерим с объемом вычислений при определении собственных чисел матрицы А. Знание собственных чисел матрицы А позволяет вынести заключение об устойчивости ЭЭС, тогда как знание коэффициентов характеристического уравнения потребует ещё значительного объема вычислений, чтобы отве­тить на вопрос об устойчивости ЭЭС. Именно поэтому с 60-х годов про­шлого столетия большое внимание уделялось разработке методов и алго­ритмов анализа корней характеристического уравнения без вычисления его коэффициентов.

2. Анализ корней характеристического уравнения

Можно указать следующие подходы, с помощью которых можно от­ветить на вопрос: какие знаки у вещественных частей корней характери­стического уравнения? Это непосредственное вычисление корней, приме­нение алгебраических критериев, частотных критериев, метода конформ­ных отображений.

1. Вычисление корней характеристического уравнения

При невысокой степени характеристического уравнения (3.4) для вы­числения его корней можно использовать способы вычисления корней обычного алгебраического уравнения. При высокой степени алгебраиче­ского уравнения (уже при п > 4) прямых способов вычисления его корней нет. Поэтому при больших п проблема вычисления корней характеристи­ческого уравнения рассматривается иначе. Дело в том, что корни характе­ристического уравнения (3.3) являются собственными значениями (числа­ми) матрицы А. Проблема вычисления собственных значений больших матриц продолжает активно исследоваться, и появились эффективные ме­тоды её решения. Следует отметить, что вычисление всех собственных значений больших матриц - трудоемкая задача.

Если необходимо только вынести заключение об устойчивости систе­мы, то путь непосредственного вычисления корней характеристического уравнения, скорее всего, не лучший. Однако, если необходимо проанали­зировать весь спектр корней характеристического уравнения, влияние на них параметров схемы и режима, законов регулирования, то такой подход может оказаться наилучшим.

2. Анализ корней характеристического уравнения с помощью алгебраических критериев

Корни характеристического уравнения (3.4) полностью определяются коэффициентами a_t этого уравнения. Идея алгебраических критериев со­стоит в том, чтобы указать систему правил, которым должны удовлетво­рять коэффициенты характеристического уравнения a_r i = 0,n , чтобы

корни уравнения имели только отрицательные вещественные части. Сами корни при этом не вычисляются. Предложено несколько таких критериев. Наиболее известными являются критерий Рауса и критерий Гурвица. Рас­смотрим один из них.

Критерий Гурвица. Для того чтобы корни характеристического урав­нения имели только отрицательные вещественные части, необходимо, что­бы все коэффициенты уравнения были положительны, a_t > 0, i = 0, п, и, кроме того, определитель Гурвица и все его диагональные миноры были также положительны, А; > 0, /' = 1, п.

Правило составления определителя Гурвица состоит в следующем. По главной диагонали определителя выписываются коэффициенты характери­стического уравнения, начиная с а₁ до а_п . Затем столбцы определителя

дополняются коэффициентами характеристического уравнения вверх от диагонали по возрастающим индексам, вниз - по убывающим. Если теку­щий индекс коэффициента становится меньше 0 или больше п, то соответ­ствующий элемент определителя полагается равным 0.

Например, при п = 4 определитель Гурвица Л_п будет иметь вид:

а, й₃ 0 0

а₀ а₂ а₄ 0

0 а₀ а₂ а₄

Диагональные миноры получаются из главного определителя выделе­нием 1,2,...,п строк и столбцов. Для рассматриваемого примера диаго­нальные миноры будут равны:

a j а₃

Д1 — ; Д2 —

а_х а_ъ 0

; Д₃ = а₀ а₂ а₄; Д₄ = А_п = а_п • А_п__{. 0 <2j а₃

Вычисление диагональных миноров можно осуществить с помощью метода Гаусса с делением на шаге. Пусть выполнен прямой ход Гаусса по матрице определителя Гурвица и а_х,а₂,...,а_п являются ведущими эле­ментами на соответствующих шагах вычислительного процесса Г аусса, то­гда диагональные миноры будут равны

А,- = П⁵/’ i = ^’ⁿ-

7=1

Поскольку величины диагональных миноров не нужны, а нужно толь­ко, чтобы они все были положительными, то для этого достаточно, чтобы все ведущие элементы вычислительного процесса Гаусса были положи­тельны.

3. Анализ корней характеристического уравнения с помощью частотных критериев

Существует несколько частотных критериев: критерий Михайлова, критерий Найквиста, метод D-разбиения (критерий Неймарка). Рассмотрим один из них.

Метод D-разбиения. Коэффициенты характеристического уравнения

4. связаны определенными соотношениями с параметрами электриче­ской системы. Поэтому изменение того или иного параметра электриче­ской системы влечет за собой изменение коэффициентов и, следовательно, корней характеристического уравнения. Если параметры системы изменять в каких-либо пределах, то можно установить область значений этих пара­метров, при которых все корни характеристического уравнения будут иметь только отрицательные вещественные части - область устойчивости. А также найти значения параметров системы, при которых получаются чи­сто мнимые корни - граница области устойчивости. В методе D-разбиения поступают наоборот. В характеристическом уравнении D(/?) = 0 заме­няют р чисто мнимым корнем, р = усо и, задаваясь различной величиной со в пределах от-оо до +оо, находят граничные значения интересую­щих параметров системы.

Допустим, что среди параметров электрической системы два парамет­ра К_х, К₂, входящие в характеристическое уравнение линейно, подлежат

выбору, а остальные параметры заданы. Преобразуя уравнение D{p) = 0,

можно выделить эти параметры:

Л(р)а:, + ^₂(р)а:₂ = Л(р)'

Полагая р = j со и отделяя вещественную часть от мнимой, получим систему двух уравнений с интересующими нас параметрами системы: |а₁₁(со)^₁+а₁₂(со)^₂ = а₁₀(со);

Г^а21 (^Ю)^1 ^{+ а}22 (^Ю)К-2 = ^а20 (^Ю)’

где

^а\ 1 (®) ⁺ J^a21 (^Ю) ⁼ ^ 1 (У®) ’

а_п (со) + j а 22 (со) = А₂ (у со);

а₁₀(со) + уа₂₀(со) = ^о(Ую)-

Решая систему уравнений (3.5) методом Крамера, найдем параметри­ческие уравнения границы D-разбиения:

' Л|(ю)

' ^д(“) '

<

Л,(ю)

²" Д(о) ‘

По этим выражениям, задаваясь со от -оо до +оо , можно построить границу D-разбиения в плоскости параметров К_{, К₂ (рис. 3.1).

Рис. 3.1. Область устойчивости Рис. 3.2. Область устойчивости

в плоскости параметров ЭЭС в плоскости корней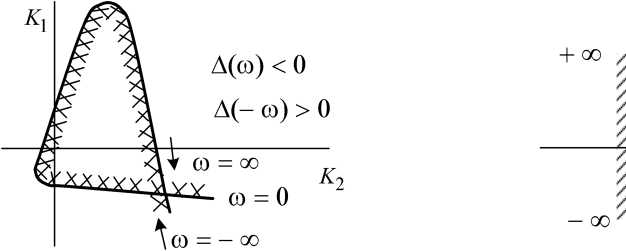

При изменении со от -оо до +оо область устойчивости в плоскости корней характеристического уравнения (рис. 3.2) лежит слева от направ­ления движения. При этом левая сторона границы области отмечена штри­ховкой.

а

О)

Для определения области устойчивости в плоскости параметров в об­щем случае нужно проверить устойчивость электрической системы с по­мощью какого-либо другого критерия (например, с помощью критерия Гурвица) при таких значениях параметров К_х, К₂, при которых соответ­

ствующая точка находилась бы внутри области, подозреваемой на область устойчивости.

В рассматриваемом случае, когда К_], К₂ входят линейно в характери­стическое уравнение, существует правило, позволяющее однозначно уста­новить область устойчивости, а именно:

• главный определитель системы уравнений (3.5) Д(со) следует состав­лять так, чтобы в первом столбце его стояли коэффициенты при том параметре, который будет откладываться по горизонтальной оси;

• при возрастании © от -оо до +оо границу D-разбиения следует штриховать слева от направления движения, если А (со) > 0, и справа,

если А(со)<0;

• область, окаймленная штриховкой, будет областью устойчивости.

В рассматриваемом случае А (со) должен быть составлен так:

А (со) =

«12 (со) а_х J (со)

^а22 (®) ^21 (®)

Для обеспечения запаса устойчивости значения параметров К_х, К₂ нужно выбирать так, чтобы соответствующая точка находилась внутри об­ласти устойчивости на некотором расстоянии от ее границы.

3.4.4. Анализ корней характеристического уравнения с использованием конформных отображений

Алгебраические критерии применимы лишь в том случае, если харак­теристическое уравнение (3.3) приведено к виду (3.4), т. е. вычислены все коэффициенты a_t. Что касается частотных критериев, то эффективность

их применения без приведения характеристического уравнения к виду (3.4) будет гораздо хуже. Поэтому был предложен другой подход к задаче ана-

лиза корней характеристического уравнения, а точнее к анализу собствен­ных чисел матрицы А.

Вычисляется вспомогательная матрица

В = Е + 2(А-Е)~\ где Е - единичная матрица.

D

Вычисляется наибольшее собственное значение X _тах этой матрицы.

При этом,

I ^в

max

если

<1, то все корни характеристического уравнения будут

иметь только отрицательные вещественные части - ЭЭС устойчива;

л в

'мпах

если

= 1, то хотя бы один корень характеристического уравне­ния является чисто мнимым - граница области устойчивости;

1^В

^дтах

если

>1, то хотя бы один корень характеристического уравне­ния имеет положительную вещественную часть - ЭЭС неустойчива.

Обычно для определения максимального по модулю собственного значения рекомендуется степенной метод. Однако этот метод плохо схо­дится, если максимальное по модулю собственное значение является ком­плексным числом, если оно кратное, если имеются два максимальных по модулю собственных значения противоположного знака или имеется соб­ственное значение, близкое по модулю к максимальному собственному значению.

Задачу можно решить с помощью хорошо разработанного QR- алгоритма, если его применить к матрице С = В~¹. Минимальное по мо­дулю собственное значение матрицы С будет равно l/A,^_ax . Поиск соб­ственных значений матрицы ^-алгоритм начинает с наименьшего соб­ственного значения.