6. Характеристики мощности и статическая устойчивость комплексных нагрузок узлов

   1. Характеристики мощности комплексных нагрузок

Нагрузки узлов электрических систем являются комплексными, т.е. состоят из большого числа различных потребителей. Состав потребителей, входящих в комплексную нагрузку, может меняться в довольно широких пределах в зависимости от района. Примерный состав городской нагрузки,

х„ 38

M = P/&_0tt = Re(u²/zy 110

X, 117

J_ 124

dt 132

^р р„, 159

р„(^и) ^z,~ в Л^и) 214

Л,(ю) 231

GKID^ а 296

екп>= : 338

(2Х2Ж- 345

В случае сложной комплексной нагрузки выявить характеристику P(U,s) отдельного асинхронного двигателя, необходимую для анализа его

устойчивости, практически невозможно. Для решения вопроса об устойчи­вости двигателей, входящих в состав комплексной нагрузки, используют статические характеристики комплексной нагрузки по напряжению Р_н (и), Q_H (U) (рис. 2.16). Прогиб характеристики Q_H (U) образуется за

счёт асинхронных двигателей.

Рис. 2.16. Статические характеристики комплексной нагрузки по напряжению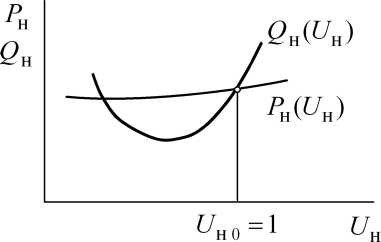

Зависимости P_H(U), 0_Н(С/) получаются экспериментально (в зоне

рабочих напряжений) или с помощью специальных расчётов и представ­ляются либо таблично, либо в форме полиномов. Например, типовая нагрузка шин 110 кВ:

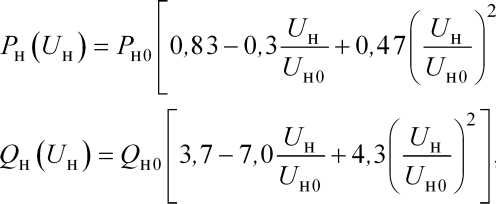
где t/_H0, Р_н0, Q_h0- напряжение и составляющие мощности комплексной нагрузки в некотором исходном режиме.

Очень важным свойством комплексной нагрузки является то, что при снижении напряжения в зоне рабочих напряжений (0,9^1,1) уменьшается потребление ею активной и реактивной мощности, что задерживает сни­жение напряжения. Это свойство называется регулирующим эффектом нагрузки. Величина регулирующего эффекта оценивается величиной про­изводных в рабочей точке и в относительных единицах вблизи U_H() со-

• ставляет:

  = 0,3-5-0,75;-^- = 1,5-5-3,5 . dU dU

1. Критерий статической устойчивости комплексной

• >0

dU

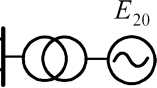Применение критерия рассмотрим на примере двухмашинной схемы, изображённой на рис. 2.17.

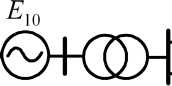
U

На рис. 2.18. приведены исходная и расчётная схемы замещения рас­сматриваемой системы. Для простоты в схемах замещения не учитываются проводимости на землю элементов системы.

U

'10

"20

-о

ьн

и

вв(и)

р„(^и) ^z,~ в Л^и)

Рис. 2.18. Исходная и расчётная схемы электрической системы

Генераторы станций в исходной схеме замещения должны быть пред­ставлены ЭДС Е_х в зависимости от типа АРВ. Величины ЭДС опреде­ляются расчётом исследуемого на устойчивость установившегося режима.

Выполнив преобразование исходной схемы, придём к расчётной схеме замещения, где

Z.Zo

Z = R + jX =

Zj + z₂

• _ £iqZ₂ +£20^1 . ⁰ Z_t + Z₂

Напряжение на шинах нагрузки и эквивалентная ЭДС в расчётной схеме замещения связаны соотношением

PJU)-jQJU)

U + Z-

и

Задаваясь напряжением на шинах нагрузки и определяя по статиче­ским характеристикам Р_я, Q_H. по приведённой формуле можно построить

зависимость E(U) (рис. 2.19).

Рис. 2.19. Зависимость Е(и) и критическое напряжение узла нагрузки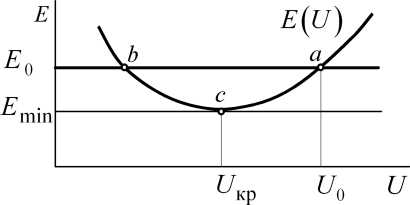

При известном уровне эквивалентной ЭДС Е ₀ возможные режимы на характеристике E(U) определяются точками а и Ь. Точка а, вкото-

dE

рой >0, соответствует устойчивому режиму. Точка b - неустойчи-

dU

вому. Предельный по статической устойчивости режим соответствует точ- dE

ке с, в которой = 0 и Е₀=Е_т-_т. Условием существования режимов

dU

будет: E₀>E_min.

dE

Уровень напряжения, соответствующий условию = 0, является

критическим, С/_кр. При более низком напряжении устойчивость нагрузки

узла, а следовательно, и системы в целом нарушается. При этом двигатели, входящие в состав комплексной нагрузки узла, останавливаются.

Запас статической устойчивости нагрузки, %, определяется по выра­жению

_к ^и°~^и*р₁₀₀, и₀

Для нормальных режимов запас статической устойчивости нагрузки должен быть не менее 15 %.

3. Критерий статической устойчивости комплексной

dAQ

нагрузки < 0

Для расчётной схемы, приведенной на рис. 2.18, поток мощности, приходящий из сети в узел нагрузки, учитывая (2.11), можно выразить так:

PJU) = -U² у -sina + Eld • v-sin(5 + a);

(2.16)

Q_C(U) = -Id¹ у -cos a + EU -^^08(5 + a),

где у = l/|z|; a = arctg(i?/X).

Последовательность расчётов при определении U_Kp будет следующей:

• задаётся модуль напряжения на шинах нагрузки и по статической характеристике Р_н (£/) определяется Р_н ;

• положив Р_с = Р_н, из первого уравнения (2.16) определяется угол 5;

• при заданном U и известном 5 из второго уравнения (2.16) опре­деляется реактивная мощность Q_c, поступающая из сети в узел;

• задаётся новый уровень напряжения узла, и расчёты повторяются.

По результатам расчётов можно построить зависимость AQ(U) = Q_C(U)-Q„ (U)

и определить критическое напряжение С/_кр? соответствующее максимуму

этой зависимости, когда ^Я- = о (рис 2.20).

dU

Рис. 2.20. Определение критического напряжения узла нагрузки по критерию dkQ/dU <0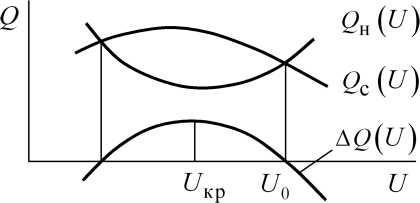

Контрольные вопросы

1. Простейшая ЭЭС с неявнополюсными генераторами и её векторная диаграм­ма токов и напряжений. Определение ЭДС.

2. Характеристика активной мощности, отдаваемой генераторами, работающи­ми в простейшей системе. Предел передаваемой мощности. Условие существования установившегося режима. Практический критерий статической устойчивости.

3. Векторная диаграмма токов и напряжений простейшей ЭЭС с явнополюсны­ми генераторами. Определение ЭДС. Характеристика активной мощности.

4. Приближённый учет действия систем регулирования возбуждения генерато­ров при рассчётах установившихся режимов.

5. Как зависит в простейшей системе предел передаваемой мощности генерато­ра от статизма его системв1 регулирования возбуждения?

6. Характеристики активных и реактивных мощностей генераторов, работаю­щих в сложной системе и процедура их получения.

7. Характеристика мощности асинхронного двигателя, вытекающая из его Г- образной схемы замещения. Максимальная мощность. Прямые критерии устойчивости. Критическое напряжение.

8. Статические характеристики мощности комплексных нагрузок узлов по напряжению. Регулирующие эффекты комплексной нагрузки.

9. Определение критического напряжения узла нагрузки в двухмашинной си­стеме по критерию dEjdU > 0.

10. Определение критического напряжения узла нагрузки в двухмашинной си­стеме по критерию dkQ/dU <0.

2. АНАЛИЗ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ СИСТЕМ С ПОМОЩЬЮ ЛИНЕАРИЗОВАННЫХ УРАВНЕНИЙ

ЗЛ. Метод малых колебаний

По определению, статическая устойчивость - это способность ЭЭС возвращаться после временного приложения малых возмущений к исход­ному или близкому к исходному положению равновесия. Так как при ма­лых возмущениях отклонения параметров режима от их исходных значе­ний также малы, то можно не считаться с нелинейными зависимостями между параметрами режима и принять их линейными. При этом переход­ные процессы в ЭЭС будут описываться системой линейных дифференци­альных уравнений, которую исследовать проще. В этом и состоит идея так называемого метода малых колебаний или метода линеаризованных урав­нений.

В общем случае при исследовании статической устойчивости электро­энергетической системы методом малых колебаний необходимо:

Z составить систему уравнений, описывающую переходные про­цессы в ЭЭС;

•S линеаризовать составленную систему уравнений в точке исследу­емого на устойчивость режима;

•S определить характеристическое уравнение системы линеаризо­ванных дифференциальных уравнений в нужной форме;

•S исследовать корни характеристического уравнения.

2. Анализ статической устойчивости

сложной электроэнергетической системы методом малых колебаний

Для исследования статической устойчивости сложной электрической системы необходимо составить систему уравнений, описывающую пере­ходные процессы, которая будет подобна (1.86). Так как исследуется

устойчивость допустимых установившихся режимов при малых (теорети­чески бесконечно малых) возмущениях, то в математическое описание пе­реходных процессов не нужно включать функции, задающие технические ограничения, какие-то релейные переключения и т. п., что может про­явиться только при больших возмущениях.

После линеаризации нелинейных зависимостей путем разложения их в ряд Тейлора с точностью до линейных членов ряда систему уравнений (1.86) можно записать так: dAX

dF dF = —AX + — AY;

(3.1)

dt dX dY

0 = —AX + — AY,

dX dY

где

	" dF{	dFx "			' dFx	dFx “
dF _	dx j	dxn		dF _		дУт
dX ~	dF n	dF n	У	dY ~	dFn	dF 11 п
	dx j	dxn_			_ dy\	дУт_
	~ дФх	dФ			~дФ1	dФi
dO _	dx j	dxn		dФ _	d}’\	дУт
dX	сФ ^ ^m	dФ		dY	дФт	dФ w п,
	dx j	dxn _			ду i	дУт
АХ = [Axj ••• Ахп		\T:		ДГ = [ДЛ-Ду„]Г.

Здесь Ax j = Xj -Xj₀, Ay j = y- - yj₀ - отклонения параметров режима x_if у j от их значений x_i0, yj₀ в режиме, в котором проверяется устойчи­вость системы.

Все частные производные должны быть вычислены в точке линеари­зации, т. е. при значениях параметров режима, равных x_i0, yj₀.

Исключив из системы уравнений (3.1) переменные A Y, придем к си­стеме линейных дифференциальных уравнений порядка п, в стандартной форме

d АХ

dt

дФ_

dY

= А- АХ, (3.2)

-1

дФ

, dF dF где А =

дХ dY

дХ

Характеристическим уравнением системы линейных дифференциаль­ных уравнений (3.2) является

\А-рЕ\ = 0, (3.3)

где \А- рЕ\ - характеристический определитель; Е— единичная матри-

ца; р - вспомогательная переменная.

В развернутом виде характеристическое уравнение представляет со­бой обычное алгебраическое уравнение для сложных электрических си­стем высокой степени:

D(р) = @ор^п + &\р^п ^ + • • • + a_n_iP^ + а_п = 0. (3-4) Решением системы дифференциальных уравнений (3.2) (при отсут­ствии кратных корней) будет набор функций

^A*;(/) ⁼ Z^C^^e/y> i = 1, п. к=\

Здесь С_ik - постоянные интегрирования, определяемые исходя из началь­ных условий; р_к= а_к + /со_к - корни характеристического уравнения (3.3) или (3.4).

Так как C_ik не зависят от времени, то характер изменения Ах j (/)

будет зависеть от функций е^Рк , которые называют собственными гармо­никами.

_еРк¹ ₌₆^(ак +^к)⁽ _=е^ак<^®к>

Множитель e^J(!>k' определяет частоту колебаний, а множитель е^ик' - изменение во времени амплитуды к-Vi гармоники.

Очевидно, что если действительные части всех корней характеристи­ческого уравнения будут отрицательны, ос^ < О, к-\,п , то возникшие от­клонения параметров режима с течением времени будут затухать. В систе­ме восстановится прежний установившийся режим. Электроэнергетиче­ская система устойчива.

Если действительная часть хотя бы одного корня характеристического уравнения будет положительна, то после какого-либо возмущения в систе­ме будут возникать колебания параметров режима с нарастающей ампли­тудой. Электроэнергетическая система неустойчива.

Возможность исследования устойчивости физических систем при ма­лых возмущениях с помощью линеаризованных уравнений была доказана А. М. Ляпуновым, 1893 г.