3 Моделирование тенденции временного ряда показателей

Так как сезонных колебаний и циклов при анализе динамики временного ряда не выявлено, то для аналитического выравнивания временного ряда применим линейную модель: y^ = a + bt

Таблица 1.5

n	t	y(t)	εt	Пов-ные точки	εt2	(εt - εср.)2	(εt - εt - 1)2	εt εt - 1	|εt/yt|
1	1	176693,6	107567,033	-	1,157E+10	1,157E+10	-	-	0,608777
2	2	312950	51702,3788	0	2,673E+09	2,673E+09	3120859560	5,561E+09	0,16521
3	3	412089,3	-41279,3752	0	1,704E+09	1,704E+09	8645606566	-2,13E+09	0,100171
4	4	535204,4	-110285,329	0	1,216E+10	1,216E+10	4761821679	4,553E+09	0,206062
5	5	708062,1	-129548,683	1	1,678E+10	1,678E+10	371076805	1,429E+10	0,182962
6	6	934328,9	-95402,937	0	9,102E+09	9,102E+09	1165931974	1,236E+10	0,102109
7	7	1295649,9	73797,0091	0	5,446E+09	5,446E+09	2,8629E+10	-7,04E+09	0,056958
8	8	1645753	231779,055	1	5,372E+10	5,372E+10	2,4958E+10	1,71E+10	0,140835
9	9	1519446,3	-86648,6988	1	7,508E+09	7,508E+09	1,014E+11	-2,01E+10	0,057026
10	10	1796535,6	-1680,45273	-	2823921,4	2823921,4	7219602839	145609042	0,000935
		Σ	9,6043E-10	3	1,207E+11	1,207E+11	1,8027E+11	2,475E+10	1,621045
		среднее	9,6043E-11

Рассчитанные а = -122994,5 и b = 192121,1

Уравнение линейного тренда будет иметь вид: y^ = -122994 + 192121·t

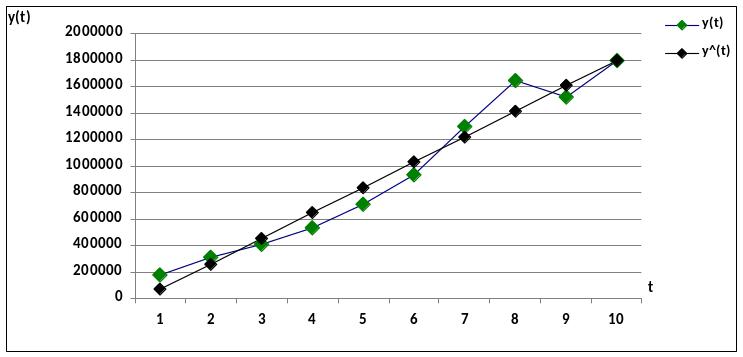
Рисунок 1.4 – Трендовая модель

Построенную модель проверим на адекватность и оценим ее точность.

Трендовая модель является адекватной, если для остаточной последовательности характерны следующие свойства:

1) Случайность колебаний уровней остаточной последовательности.

Для проверки данного свойства воспользуемся критерием пиков. Построим график остатков (рисунок 1.5)

поворотная точка;

m = 3

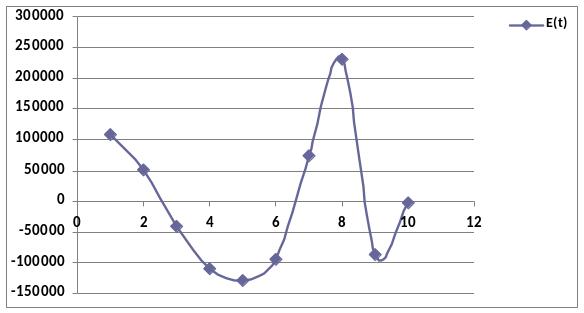
Рисунок 1.5 – Ряд остатков

Так как неравенство m > 2 выполняется, значит можно сделать вывод, что колебания уровней остаточной последовательности являются случайными.

2) Соответствие распределения случайной компоненты нормальному закону распределения:

Для проверки данного свойства воспользуемся RS - критерием:

Таблица 1.6 – Расчет значения R/S_ε

εmax	εmin	R	Sε	R/Sε	R/Sтабл.
231779,0552	-129548,683	361327,7382	115793,6741	3,12044454	(2,67; 3,57)

Так как вычисленное значение R/S - критерия попадает в интервал табличных (критических) границ, то гипотеза о нормальности распределения принимается.

3) Равенство математического ожидания случайной компоненты нулю:

Для проверки данного свойства применим t-критерий Стьюдента:

S_ε = 115793,6741

t_расч. = 2,62289E-15

t_α = 2,2622

Расчётное значение t больше табличного значения ta статистики Стьюдента с уровнем значимости a = 0,05 и числом степеней свободы n - 1 = 9, то выдвинутая гипотеза о равенстве нулю математического ожидания случайной компоненты не принимается, тренд есть.

4) Независимость значений уровней случайной компоненты:

Т.е. проверка отсутствия существенной автокорреляции в остаточной последовательности может осуществляться по d-критерию Дарбина-Уотсона:

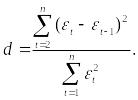
d = 1,493848865

d₁ = 0,88

d₂ = 1,32

Т.к. d2< d < 2 , то ряд остатков не коррелирован.

Таким образом, при проверке свойств остаточной последовательности, получили, что все свойства выполняются, а значит можно сделать вывод об адекватности линейной модели.

Для оценки точности линейной модели рассчитаем следующие параметры линейного тренда:

- Линейный коэффициент парной корреляции: r_ty = 0,980755831, следовательно, линейная связь весьма высокая.

- Коэффициент детерминации: R2 = 0,961882 Коэффициент детерминации R2 показывает, что около 96,19% изменения результативного признака y(t) объясняется временным диапазоном.

Для оценки качества построенной модели рассчитаем среднюю ошибку аппроксимации `A = 16,2104481

- Средняя ошибка аппроксимации `А =16,21% не превышает 25%, а значит линейную модель регрессии можно считать приемлемой для анализа связи между фактором (t) и результативным показателем (y).

Среднее квадратическое отклонение: Sy = 122817,7383

Средняя квадратическая ошибка: S = 115793,6741

: