1. Случайные события, определение. Типы: достоверное, совместимое, взаимодополнительное, благоприятствующие, полная группа событий. Привести примеры.

  Познание действительности в естественных науках происходит в результате испытаний (эксперимента, наблюдений, опыта).      Испытанием или опытом называется осуществление какого-нибудь определенного комплекса условий, который может быть воспроизведен сколь угодно большое число раз.      Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания (опыта).      Таким образом, событие рассматривается как результат испытания.      Пример. Бросание монеты – это испытание. Появление орла при бросании – событие.      Наблюдаемые нами события различаются по степени возможности их появления и по характеру их взаимосвязи.      Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.      Пример. Получение студентом положительной или отрицательной оценки на экзамене есть событие достоверное, если экзамен протекает согласно обычным правилам.      Событие называется невозможным, если оно не может произойти в результате данного испытания.      Пример. Извлечение из урны белого шара, в которой находятся лишь цветные (небелые) шары, есть событие невозможное. Отметим, что при других условиях опыта появления белого шара не исключается; таким образом, это событие невозможно лишь в условиях нашего опыта.      Далее случайные события будем обозначать большими латинскими буквами A,B,C... Достоверное событие обозначим буквой Ω, невозможное – Ø.      Два или несколько событий называются равновозможными в данном испытании, если имеются основания считать, что ни одно из этих событий не является более возможным или менее возможным, чем другие.      Пример. При одном  бросании игральной кости появление 1, 2, 3, 4, 5 и 6 очков - все это события равновозможные. Предполагается, конечно, что игральная кость изготовлена из однородного материала и имеет  правильную форму.      Два события называются несовместными в данном испытании, если появление одного из  них исключает появление другого, и совместными в противном случае.      Пример.  В ящике имеются стандартные и нестандартные детали. Берем  на удачу одну деталь. Появление стандартной детали исключает появление нестандартной детали. Эти события несовместные.      Несколько событий образуют полную группу событий в данном испытании, если в результате этого испытания обязательно наступит хотя бы одно из них.      Пример. События из примера образуют полную группу равновозможных и попарно несовместных событий.      Два несовместных события, образующих полную группу событий в данном испытании, называются противоположными событиями.      Если одно из них обозначено через A, то другое принято обозначать через  (читается «не A»).      Пример. Попадание и промах при одном выстреле по цели - события противоположные.

     Вероятность события – численная мера возможности его наступления.      Событие А называется благоприятствующим событию В, если всякий раз, когда наступает событие А, наступает и событие В.      События А₁, А₂, ..., А_n образуют схему случаев, если они:      1) равновозможны;      2) попарно несовместны;      3) образуют полную группу.      В схеме случаев (и только в этой схеме) имеет место классическое  определение вероятности P(A) события А. Здесь случаем называют каждое из событий, принадлежащих выделенной полной группе равновозможных и попарно несовместных событий.      Если n – число всех случаев в схеме, а m – число случаев, благоприятствующих событию А, то вероятность события А определяется равенством:           Из определения вероятности вытекают следующие ее свойства:      1. Вероятность достоверного события равна единице.      Действительно, если событие достоверно, то каждый случай в схеме случаев благоприятствует событию. В этом случае m = n и, следовательно,           2. Вероятность невозможного события равна нулю.      Действительно, если событие невозможно, то ни один случай из схемы случаев не благоприятствует событию. Поэтому  m=0 и, следовательно,           Вероятность случайного события есть положительное число,  заключенное между нулем и единицей.      Действительно, случайному событию благоприятствует лишь часть из общего числа случаев в схеме случаев. Поэтому 0<m<n, а, значит, 0<m/n<1 и, следовательно, 0 < P(A) < 1.      Итак, вероятность любого события удовлетворяет неравенствам      0 ≤ P(A) ≤ 1.      В настоящее время свойства вероятности определяются в виде аксиом, сформулированных А.Н. Колмогоровым.      Одним из основных достоинств классического определения вероятности является возможность вычислить вероятность события непосредственно, т.е. не прибегая к опытам, которые заменяют логическими рассуждениями.

Операции над событиями

Часто бывает полезно наглядно представить события в виде диаграммы Эйлера — Венна. Изобразим все пространство элементарных исходов прямоугольником (рис. 1). При этом, каждый элементарный исход ω соответствует точке внутри прямоугольника, а каждое событие A — некоторому множеству точек, этого прямоугольника.

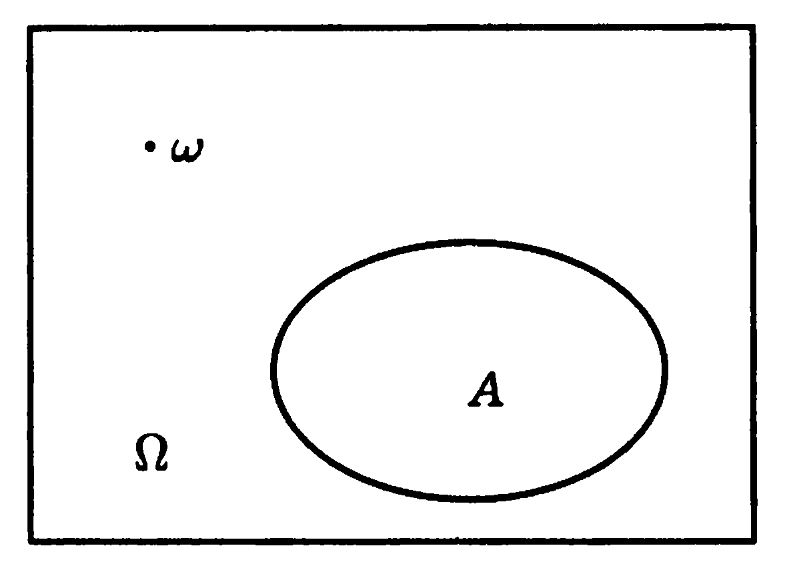
Рис. 1. Изображение диаграммы Эйлера-Венна

Рассмотрим теперь операции над событиями, которые совпадают с операциями над множествами.

Определение

Пересечением (произведением) двух событий A и B называют событие, обозначаемое A∩B или AB, происходящее тогда и только тогда, когда одновременно происходят оба события A и B, т.е. событие, состоящее из тех и только тех элементарных исходов, которые принадлежат и событию A, и событию B.

События A и B называются несовместными, или непересекающимися, если их пересечение является невозможным событием, т.е. если A∩B=∅.

События A1,A2,…,An называют попарно несовместными, если для любых i≠j, где i,j=1,n¯¯¯¯¯, события Ai и Aj несовместны.

В противном случае события называют совместными, или пересекающимися.

Определение

Объединением (суммой) двух событий A и B называют событие, обозначаемое A∪B, происходящее тогда и только тогда, когда происходит хотя бы одно из событий A или B, т.е. событие состоит из элементарных исходов, которые принадлежат хотя бы одному из множеств A или B.

Если события A и B несовместимы, то для обозначения могут использововать символ «+».

Например, поскольку невозможное событие ∅ несовместно с любым событием A, то

∅∪A=∅+A=A.

Аналогично определяют понятия произведения и суммы событий для любого конечного числа событий и даже для бесконечных последовательностей событий. Так, событие

A1A2…An=∩ni=1Ai

состоит из элементарных исходов, принадлежащих всем событиям Ai,i=1,n¯¯¯¯¯, а событие

A1∪A2∪…∪An=∪ni=1Ai

состоит из элементарных исходов, принадлежащих хотя бы одному из событий Ai,i=1,n¯¯¯¯¯.

В частности, события A1,A2,…,An называют попарно несовместными, если

AiAj=∅

для любых i,j=1,n¯¯¯¯¯,i≠j, и несовместными в совокупности, если

A1A2…An=∅.

Определение

Разностью двух событий A и B называют событие, обозначаемое A∖B, происходящее тогда и только тогда, когда происходит событие A и не происходит событие B, т.е. состоит из тех элементарных исходов, которые принадлежат событию A и не принадлежат событию B

Определение

Дополнением события A называют новое событие, обозначаемое A¯¯¯, происходящее тогда и только тогда, когда не происходит событие A. Так событие A¯¯¯можно записать в виде:

A¯¯¯=Ω∖A.

Событие A¯¯¯ называют событием, противоположным событию A.

Определение

Событие A включено в событие B, если появление за собой события A обязательно влечет за собой наступление события B, или каждый элементарный исход события A принадлежит и событию B.

Приоритеты операций

Если некоторое событие записано в виде нескольких операций над различными событиями, то сначала выполняется операция дополнения, затем умножения, и, наконец, сложение и вычитание (слева направо).

Скобки могут увеличить приоритет любой из операций.

Пример

Рассмотрим устройство из n элементов. Элементы соединены последовательно, если устройство прекращает функционировать при отказе любого из элементов, и соединены параллельно, если прекращение функционирования наступает только при отказе n элементов (рис. 1а, 1б соответственно).

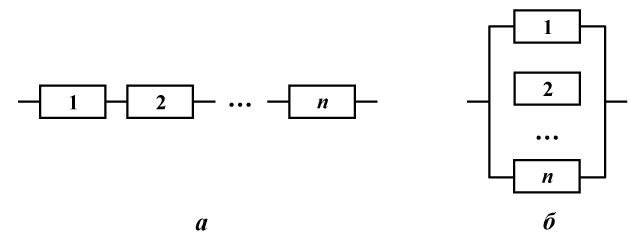
Рис 1. Последовательное и параллельное соединения

Обозначим A событие означающее отказ системы, а Ai — отказ i-го элемента (i=1,n¯¯¯¯¯). Тогда для последовательного соединения событие A представимо в виде:

A=A1∪A2∪…An,

а для параллельного соединения

A=A1∩A2∩…An.

Очевидно, что при параллельном соединении элементов событие A включено в каждое из событий Ai,i=1,n¯¯¯¯¯, а при последовательном соединении любое событие Ai,i=1,n¯¯¯¯¯ включено в событие A.

3. Статистическая вероятность, геометрическая вероятность. Классическая формула вероятности

Итак, статистическая вероятность случайного события А равна относительной частоте появления этого события в ряде испытаний, т.е.

,

где m – число испытаний, в которых появилось событие А;

n – общее число испытаний.

Согласно геометрическому определению,

вероятность случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области, т.е.

.

Классическая формула вероятности

Если множество элементарных событий Ω={ω1,ω2,…ωN},конечно и все элементарные события равновозможны, то такая вероятностная схема носит название классической. В этом случае вероятность Р{А} наступления события А, состоящего из М элементарных событий, входящих в Ω, определяется как отношение числа М элементарных событий, благоприятствующих наступлению события А, к общему числу N элементарных событий. Эта формула носит название классической формулы вероятности: Р{А}= M/N.

В частности, согласно классической формуле вероятности:

Р{ωi }=1/N (i=1,2,... , N)

Р{Ω}= N/N =1

P{}=0/N =0

Теорема сложения вероятностей несовместных событий
. Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах. В частности, если два события А и B — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С. Пусть события A и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения. Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В). Доказательство С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An).

5. Условная вероятность. Теорема о вероятности совместного появления двух и более событий.

Условной вероятностью Р(В/А) называется вероятность события В, вычисленная в предположении, что событие А уже наступило.

Теорема. Вероятность совместного появления двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:      Р(А∙В) = Р(А)∙Р(В/А).                                                  (2.2)      Два события называются независимыми, если появление любого из них не изменяет вероятность появления другого, т.е.      Р(А) = Р(А/В) или Р(В) = Р(В/А).                       (2.3)      Если события А и В независимы, то из формул (2.2) и (2.3) следует      Р(А∙В) = Р(А)∙Р(В).                                                      (2.4)      Справедливо и обратное утверждение, т.е. если для двух событий выполняется равенство (2.4), то эти события независимы. В самом деле, из формул (2.4) и (2.2) вытекает      Р(А∙В) = Р(А)∙Р(В) = Р(А) ×Р(В/А), откуда Р(А) = Р(В/А).      Формула (2.2) допускает обобщение на случай конечного числа событий А₁, А₂,…,А _n:      Р(А₁∙А₂∙…∙А _n)=Р(А₁)∙Р(А₂/А₁)∙Р(А₃/А₁А₂)∙…∙Р(А _n/А₁А₂…А _n-1).

Теорема. Вероятность совместного появления двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:      Р(А∙В) = Р(А)∙Р(В/А).                                                  (2.2)      Два события называются независимыми, если появление любого из них не изменяет вероятность появления другого, т.е.      Р(А) = Р(А/В) или Р(В) = Р(В/А).                       (2.3)      Если события А и В независимы, то из формул (2.2) и (2.3) следует      Р(А∙В) = Р(А)∙Р(В).                                                      (2.4)      Справедливо и обратное утверждение, т.е. если для двух событий выполняется равенство (2.4), то эти события независимы. В самом деле, из формул (2.4) и (2.2) вытекает      Р(А∙В) = Р(А)∙Р(В) = Р(А) ×Р(В/А), откуда Р(А) = Р(В/А).      Формула (2.2) допускает обобщение на случай конечного числа событий А₁, А₂,…,А _n:      Р(А₁∙А₂∙…∙А _n)=Р(А₁)∙Р(А₂/А₁)∙Р(А₃/А₁А₂)∙…∙Р(А _n/А₁А₂…А _n-1).

 

Теоремы сложения вероятностей

Найдем вероятность суммы событий   и   (в предположении их совместности либо несовместности).

Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:

поскольку  , как это было найдено в примере 1.

Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой "Electra Ltd" оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно  . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим  . Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события   являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.

Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).

Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:

Зависимые и независимые события. Условная вероятность

Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.

Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события  , вычисленная в предположении осуществления другого события  , называется условной вероятностью события   и обозначается  .

Условие независимости события   от события   записывают в виде  , а условие его зависимости — в виде  . Рассмотрим пример вычисления условной вероятности события.

Формулы умножения вероятностей

Пусть события   и   независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий   и  .

Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Пусть события   и   зависимые, причем вероятности   и   известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие  , и событие  .

Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.

Формула полной вероятности

Теорема 2.5. Если событие   наступает только при условии появления одного из событий  , образующих полную группу несовместных событий, то вероятность события   равна сумме произведений вероятностей каждого из событий   на соответствующую условную вероятность события  :

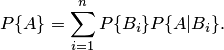
(2.1)

При этом события   называются гипотезами, а вероятности   — априорными. Эта формула называется формулой полной вероятности.

Формула Байеса

Эта формула применяется при решении практических задач, когда событие  , появляющееся совместно с каким-либо из событий  , образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез  . Априорные (до опыта) вероятности   известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности  . Для гипотезы   формула Байеса выглядит так:

Раскрывая в этом равенстве   по формуле полной вероятности (2.1), получаем

7. Формула полной вероятности. Формула Байеса.

Пусть событие А может произойти в результате осуществления одного

события из некоторой полной группы событий:

События этой группы обычно называют гипотезами.

Тогда

(формула полной вероятности), причем

формула Байеса. Пусть — полная группа событий, и — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие , если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:

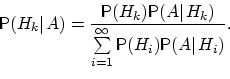
Дискретные и непрерывные случайные величины. Функции распределения случайных величин.

Одним из основных в теории вероятностей является понятие случайной величины. Случайная величина - это величина, принимающая те или иные значения в зависимости от случая. Примерами случайных величин могут быть: число выпавших очков, при подбрасывании игральной кости; число попаданий в цель при k выстрелах и т.д.  Множества всех случайных величин в зависимости от типа их распределения делится на три класса: дискретные случайные величины, непрерывные случайные величины исингулярные случайные величины. В этой статье мы рассмотрим первые два класса:дискретные случайные величины и непрерывные случайные величины. Дискретные случайные величины      Определение1: Случайная величина  называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Задание дискретной случайной величины по определению равносильно заданию закона распределения случайной величины в следующем виде:      где  Следующее утверждение отражает связь между функцией распределения дискретной случайной величины и законом распределения случайной величины.      Утверждение 1: Закон распределения и функция распределения дискретной случайной величины взаимно однозначно определяют друг друга.   Примеры дискретных случайных величин: 1) дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1 Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1.   2) дискретная биномиальная случайная величина(биномиальное распределение). Закон распределения данной дискретной случайной величины запишется следующим образом: где  Число успехов в n испытаниях схемы Бернулли имеет биномиальное распределение.   3) дискретная случайная величина Пуассона(пуассоновское распределение с параметром  ). Закон распределения дискретной случайной величины Пуассона задается следующим образом: где   - параметр.      Закон распределения случайной величины Пуассона носит название закона редких событий, поскольку оно всегда появляется там, где производится большое число испытаний, в каждом из которых с малой вероятностью происходит "редкое" событие. По закону Пуассона распределены, например, число вызовов, поступивших на телефонную станцию, число распавшихся нестабильных частиц и т.д.   4) дискретная геометрическая случайная величина (геометрическое распределение). Закон распределения геометрической дискретной случайной величины имеет вид Пусть производятся независимые испытания, причем в каждом испытании возможны два исхода - "успех" с вероятностью p или "неуспех" с вероятностью 1 - p  ,  0 < p < 1 . Обозначим через  число испытаний до первого появления "успеха", тогда  будет дискретной геометрической случайной величиной.   Непрерывные случайные величины        Определение 2: Распределение случайной величины  называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого , где   - интегрируемая по Лебегу функция. Функция   называется плотностью распределения случайной величины  .      Теорема 1: Для того чтобы случайная величина   была непрерывной случайной величиной, необходимо и достаточно, чтобы для любого           (1)      Замечание 1: Из представления (1) видно, что функция распределения непрерывной случайной величины является непрерывной функцией.         Свойства плотности распределения: 1) 2)  почти всюду. 3)  для любых х, являющихся точками непрерывности плотности.        Теорема 2: Для того, чтобы функция p = p(x) была плотностью распределения некоторой случайной величины  , необходимо и достаточно, чтобы она удовлетворяла свойствам 1) и 2) плотности.   Примеры непрерывных случайных величин:   1) нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение). Непрерывная случайная величина   имеет нормальное (гауссовское) распределение, если её плотность распределения имеет вид      Если  , то распределение называется стандартным нормальным распределением.      Важная роль этого распределения объясняется тем, что оно обычно возникает в явлениях, подверженных действию большого числа малых случайных величин. Так, математическая теория выборочного метода в статистике для расчета некоторых показателей широко использует нормальное распределение.   2)экспоненциальная (показательная) непрерывная случайная величина(экспоненциальное распределение).  Непрерывная случайная величина   имеет экспоненциальное(показательное) распределение с параметром  , если её плотность имеет вид      Экспоненциальному распределению подчиняется время распада ядер атомов различных элементов. Оно обладает важным свойством - отсутствием последствия. Несложно убедиться в том, что вероятность распада ядра за время  при условии, что перед этим оно уже прожило время  , совпадает с безусловной вероятностью распада того же самого ядра за время . Именно это свойство и представляет собой отсутствие последствия.   3) Равномерная на [a;b] непрерывная случайная величина(равномерное на отрезке [a;b] распределение). Равномерно распределенная на отрезке [a;b] непрерывная случайная величина  имеет плотность распределения      Равномерное распределение реализует принцип геометрической вероятности при бросании точки на отрезок [a;b].

9. Операции над случайными величинами.

  Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий (в одном и том же испытании).      Сумма А₁ + А₂ + … + А_n обозначается так:       или .      Пример. Бросаются две игральные кости. Пусть событие А состоит в выпадении 4 очков на 1 кости, а событие В – в выпадении 5 очков на другой кости. События А и В совместны. Поэтому событие А +В состоит в выпадении 4 очков на первой кости, или 5 очков на второй кости, или 4 очков на первой кости и 5 очков на второй одновременно.      Пример. СобытиеА – выигрыш по 1 займу, событие В – выигрыш по 2 займу. Тогда событие А+В – выигрыш хотя бы по одному займу (возможно по двум сразу).      Произведением или пересечением нескольких событий называется событие, состоящее в совместном появлении всех этих событий (в одном и том же испытании).      Произведение В событий А₁, А₂, …, А_n обозначается так:      .      Пример. События А и В состоят в успешном прохождении I и II туров соответственно при поступлении в институт. Тогда событие А×В состоит в успешном прохождении обоих туров.      Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию. Пусть событие А есть попадание точки в область А, а событие В – попадание точки в область В. Тогда событие А+В есть попадание точки в объединение этих областей (рис. 2.1), а событие АВ есть попадание точки в пересечение этих областей (рис. 2.2). 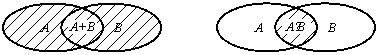          Рис. 2.1                              Рис. 2.2      Теорема. Если события A_i(i = 1, 2, …, n) попарно несовместны, то вероятность суммы событий равна сумме вероятностей этих событий:      .      Пусть А и Ā – противоположные события, т.е. А + Ā = Ω, где Ω – достоверное событие. Из теоремы сложения вытекает, что      Р(Ω) = Р(А) + Р(Ā) = 1, поэтому      Р(Ā) = 1 – Р(А).      Если события А₁ и А₂  совместны, то вероятность суммы двух совместных событий равна:      Р(А₁ + А₂) = Р(А₁) + Р(А₂) – Р(А₁×А₂).      Теоремы сложения вероятностей позволяют перейти от непосредственного подсчета вероятностей к определению вероятностей наступления сложных событий.

 

10. Ряд распределения случайной величины. Многоугольник распределения вероятностей. Закон распределения дискретной случайной величины.

Достаточно часто на практике рассматриваются такие испытания, в результате реализации которых случайным образом получается некоторое число. Например, при бросании игрального кубика выпадает число очков от 1 до 6, при взятии 6 карт из колоды можно получить от 0 до 4 тузов. За определенный промежуток времени (скажем, день или месяц) в городе регистрируется то или иное количество преступлений, происходит какое-то количество дорожно-транспортных происшествий. Из орудия производится выстрел. Дальность полета снаряда также принимает какое-либо значение случайным образом.

Во всех перечисленных испытаниях мы сталкиваемся с так называемыми случайными величинами.

Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называетсяслучайной величиной.

Понятие случайной величины играет весьма важную роль в теории вероятностей. Если «классическая» теория вероятностей изучала главным образом случайные события, то современная теория вероятностей преимущественно имеет дело со случайными величинами.

Далее будем обозначать случайные величины прописными латинскими буквами X, Y, Z и т.д., а их возможные значения – соответствующими строчными x, y, z. Например, если случайная величина имеет три возможных значения, то будем обозначать их так: ,  ,  .

Итак, примерами случайных величин могут быть:

1)           количество очков, выпавших на верхней грани игрального кубика:

2)           число тузов, при взятии из колоды 6 карт;

3)           количество зарегистрированных преступлений за день или месяц;

4)           число попаданий в мишень при четырех выстрелов из пистолета;

5)           расстояние, которое пролетит снаряд при выстреле из орудия;

6)           рост случайно взятого человека.

Можно заметить, что в первом примере случайная величина может принять одно из шести возможных значений: 1, 2, 3, 4, 5 и 6. Во втором и четвертом примерах число возможных значений случайной величины пять: 0, 1, 2, 3, 4. В третьем примере значением случайной величины может быть любое (теоретически) натуральное число или 0. В пятом и шестом примерах случайная величина может принимать любое действительное значение из определенного промежутка (а, b).

Если случайная величина может принимать конечное или счетное множество значений, то она называется дискретной(дискретно распределенной).

Непрерывной случайной величиной называется такая случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Для задания случайной величины недостаточно перечислить ее всевозможные значения. Например, во втором и в третьем примерах случайные величины могли принимать одни и те же значения: 0, 1, 2, 3 и 4. Однако вероятности, с которыми эти случайные величины принимают свои значения, будут совершенно разными. Поэтому для задания дискретной случайной величины кроме перечня ее всех возможных значений нужно еще указать их вероятности.

Соответствие между возможными значениями случайной величины и их вероятностями называют законом распределениядискретной случайной величины.

Закон распределения можно задать в виде таблицы, формулы или графически.

При табличном задании закона распределения в первой строке таблицы записываются возможные значения случайной величины, а во второй – соответствующие значениям вероятности:

X			…
p			…

 

Такая таблица называется рядом распределения дискретной случайной величины X.

Так как случайная величина в результате испытания примет одно и только одно значение, то события: Х= , Х= , …, Х= образуют полную группу. Следовательно, из следствия 1 теоремы сложения вероятностей сумма вероятностей этих событий равна единице:

+ +…+ = =1.

Для наглядности ряд распределения случайной величины можно изобразить графически. Для этого в прямоугольной системе координат по оси абсцисс ОХ  будем откладывать значения случайной величины  , k=1, 2, …,  n, а по оси ординат OY – соответствующие им вероятности  . Полученные точки соединяются отрезками прямых. Построенная таким образом фигура называется многоугольником распределения(рис.6.1).

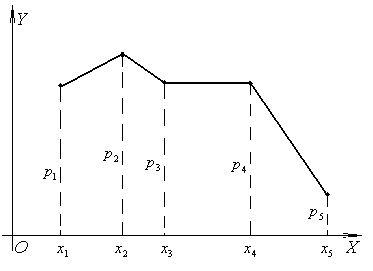
Рис. 6.1

 

Многоугольник распределения, также как и ряд распределения, полностью характеризует случайную величину. Он является одним из форм закона распределения.

Пример 6.1. Случайным образом бросается монета. Построить ряд и многоугольник распределения числа выпавших гербов.

Случайная величина, равная количеству выпавших гербов, может принимать два значения: 0 и 1. Значение 1 соответствует событию - выпадение герба, значение 0 – выпадению решки. Вероятности выпадения герба и выпадения решки одинаковы и равны . Т.е. вероятности, с которыми случайная величина принимает значения 0 и 1, равны  . Ряд распределения имеет вид:

 

X	0	1
p

 

Многоугольник распределения изображен на рис.6.2.

 

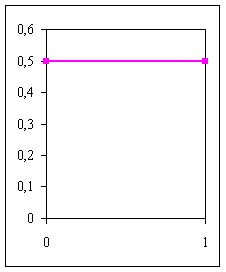
Рис. 6.2

 

Пример 6.2. Построить ряд распределения числа очков, выпавших при броске кубика.

Случайная величина Х принимает следующие значения: Х=1, 2, 3, 4, 5, 6, соответствующие выпадениям «единицы», «двойки», «тройки», «четверки», «пятерки», «шестерки» на верхней грани кубика. Так как все эти события равновозможны, то соответствующие значениям случайной величины вероятности равны  . Значит, ряд распределения запишется в таком виде:

X	1	2	3	4	5	6
p

 

Биномиальное распределение

Пример 6.3.  Построить ряд распределения числа выпавших гербов при двух бросках монеты.

Случайная величина – количество выпавших гербов при двух подбрасываниях монеты, в отличие от примера 6.1, может принимать три значения: 0, 1 и 2. Значение  =0 соответствует тому, что герб не выпал ни разу, значение  =1 соответствует выпадению герба ирешки или решки и герба, значение  =2  – выпадению двух гербов. Соответствующие вероятности можно найти по формуле Бернулли, но еще легче по теоремам умножения и сложения вероятностей:  ;   ;   .   .

Ряд распределения запишется в виде:

 

X	0	1	2
p

 

Пример 6.4. Стрелок производит три выстрела по мишени. Вероятность попадания при каждом выстреле равна 0,6. Построить ряд и многоугольник распределения числа попаданий в мишень.

Случайная величина Х – число попаданий в мишень при трех выстрелах. Возможные значения Х:  =0,  =1,  =2,  =3. Вероятность того, что произойдут k попаданий (k=0, 1,  2, 3) при трех выстрелах подсчитывается по формуле Бернулли (5.7):

   (0 k 3),

где вероятность попадания при одном выстреле p=0,6 , q  - вероятность промаха, q=1–0,6=0,4.

 

= = =0,064;

= = =3 =0,288;

= = =3 =0,432;

= = =0,216.

 

          Ряд распределения случайной величины Х имеет вид:

 

X	0	1	2	3
p	0,064	0,288	0,432	0,216

         

Можно проверить, что, действительно,  =0,064+0,288+0,432+ +0,216=1.

          Многоугольник распределения числа попаданий при трех выстрелах изображен на рис.6.3.

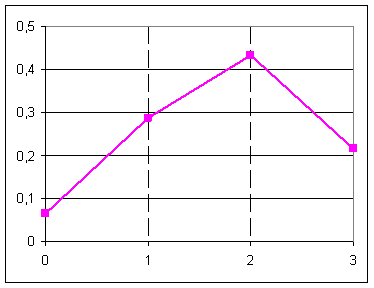
Рис. 6.3

         

          Распределения случайных величин в примерах 6.3 и 6.4 являются частными случаями биномиального распределения вероятностей при n=2 и n=3.

Биномиальным называется распределение вероятностей, определяемое формулой Бернулли:

 (0 k n).                                          (6.1)

          Формула (6.1) является аналитическим выражением биномиального закона распределения.

          По биномиальному закону распределена случайная величина Хчисла появлений события А при проведении n независимых испытаний, если вероятность появления события А в каждом испытании одинакова и равна p (q=1–p). В n испытаниях событие Аможет вообще не появиться, появиться 1 раз, 2 раза, 3 раза, …, n раз. Таким образом, возможные значения Х таковы:  =0,  =1,  =2,  =3, …,  =n. А соответствующие им вероятности подсчитываются по формуле Бернулли (6.1). Ряд распределения в этом случае будет таким:

X	0	1	2	…	k	…
p				…		…

          Cумма вероятностей, соответствующих возможным значениям случайной величины, записывается в виде бинома Ньютона:

+ + +…+ +…+ = = .   (6.2)

          Естественно, что в формуле (6.2) p+q=1 и поэтому  =1.

Геометрическое распределение

Пример 6.5. Стрелком производятся выстрелы по мишени до первого попадания. Вероятность попадания в каждом выстреле равнаp=0,6. Построить ряд распределения количества произведенных выстрелов.

Обозначим через Х дискретную случайную величину – число произведенных выстрелов до первого попадания. Возможными значениями Х являются натуральные числа  =1,  =2,  =3, …. Множество значений Х является бесконечным счетным множеством, как и ряд натуральных чисел.

Вероятность того, что случайная величина принимает значение  =1, т.е. попадание происходит при 1-м выстреле, по условию задачи равна  =p=0,6. Вероятность принятия случайной величиной значения  =2 (попадание происходит при 2-м выстреле) подсчитывается как вероятность сложного события по теореме умножения вероятностей. Непопадание в мишень в первом выстреле и попадание во втором – события независимые. Поэтому  =(1–p)p=(1–0,6)0,6=0,40,6=0,24. Аналогичным образом находятся вероятность   значения случайной величины  =3:  =(1–p)(1–p)p=(1–0,6) (1–0,6)0,6=0,40,40,6=0,096, вероятность  = 0,6= 0,6=0,0384,  = 0,6= 0,6=0,01536 и т.д.

Подсчитаем вероятность того, что случайная величина принимает значение  =k. Это означает, что попадание произошло лишь в k-м выстреле, а до этого был k-1 промах. Так как все выстрелы независимы друг от друга, то по теореме умножения вероятностей  = .

Таким образом, ряд распределения случайной величины запишется так:

X	1	2	3	4	5	…	k	…
p	0,6	0,24	0,096	0,0384	0,01536	…		…

 

Многоугольник распределения случайной величины построен на рис.6.4 до значения  =5 (множество значений дискретной случайной величины – бесконечное)

Рис. 6.4

 

Можно заметить, что ряд вероятностей, соответствующих значениям случайной величины, образует бесконечную убывающую геометрическую прогрессию со знаменателем q=0,4 и первым членом p=0,6:

0,6; 0,60,4; 0,6 ; 0,6 ; 0,6 ; … .

Поэтому распределение случайной величины в примере (6.5) называют геометрическим.

Геометрическим называется распределение вероятностей случайной величины Х, которое определяется следующим законом:

,   k1.

          Здесь p – вероятность наступления события А, q - вероятность того, что событие А не произойдет: q=1–p. Случайная величина Х определяется как число независимых испытаний, которые нужно произвести до первого появления события А.

          Очевидно, что возможными значениями Х является множество натуральных чисел xN. То, что случайная величина принимает значение  =k, означает, что в первых k-1 испытаниях А не наступило, а в k-м появилось. Вероятность этого подсчитывается по теореме умножения вероятностей для независимых событий:  = . Сумма вероятностей всех значений определяется по формуле суммы членов убывающей геометрической прогрессии со знаменателем q и первым членом p:

+ +…+ +…= = = =1.

11. Коэффициент асимметрии и эксцесс.

  Выборочным коэффициентом асимметрии называется число , определяемое формулой      .      Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона (см. далее) вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.      В случае отрицательного коэффициента асимметрии более пологий «спуск» полигона наблюдается слева, в противном случае – справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.      Выборочным эксцессом или коэффициентом крутизны называется число E^˜k, определяемое формулой      .      Выборочный эксцесс служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Ранее подчеркивалось, что эксцесс для случайной величины, распределенной нормально, равен нулю. Поэтому за стандартное значение выборочного эксцесса принимают E^˜k = 0. Если выборочному распределению соответствует отрицательный эксцесс, то соответствующий полигон имеет более пологую вершину по сравнению с нормальной кривой. В случае положительного эксцесса полигон более крутой по сравнению с нормальной кривой.

Равномерным распределением называют такое распределение случайной величины, когда она с одинаковой вероятностью может принимать любое значение в заданных пределах.

Равномерное распределение случайной величины показано на рис. 1

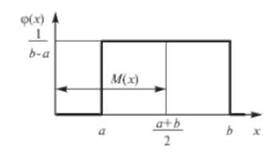
Рис. 1. Плотность вероятности (дифференциальная функция) равномерного распределения

Очевидно, что площадь под графиком этой функции равна единице и  . Поэтому    является плотностью распределения.

Плотность вероятности равномерного распределения имеет вид:

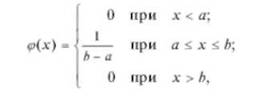
где а и Ь - параметры закона, определяющие пределы изменения случайной величины X.

 Непрерывная функция распределения в этом случае имеет вид: 

 

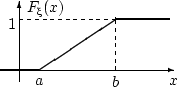
Математическое ожидание и дисперсия случайной непрерывной величины X вычисляется следующим образом:

 

M(X)=	a+b
	2

D(X)=	(b-a)^2
	12

откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]: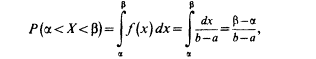 

Геометрически эта вероятность представляет  собой  площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

Пример1. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут. Найти вероятность того, что пассажир, подошедший к остановке. Будет ожидать очередной автобус менее 3 минут.

Решение:

СВ- время ожидания автобуса имеет равномерное распределение. Тогда искомая вероятность будет равна: 

Пример2. Ребро куба х измерено приближенно. Причем

  

Рассматривая ребро куба как случайную величину, распределенную равномерно в интервале (a, b), найти математическое ожидание и дисперсию объема куба.

Решение:

Объем куба- случайная величина, определяемая выражением У= Х³. Тогда математическое ожидание равно:

Дисперсия:

 

13. Распределения связанные с нормальным распределением: распределение Пирсона, Стьюдента, Фишера.

«Хи-квадрат» распределение Пирсона с f степенями свободы, распределение вероятностей суммы квадратов c^2 = X1^2+...+Xf^2, независимых случайных величин X1,..., Xf, подчиняющихся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией. Функция «Х.-к.» р. выражается интегралом Первые три момента (математическое ожидание дисперсия и третий центральный момент) суммы c2 равны соответственно f, 2f, 8f. Сумма двух независимых случайных величин c1^2 и c2^2, с f^1 и f^2 степенями свободы подчиняется «Х.-к.» р. с f^1 + f^2 степенями свободы. Примерами «Х.-к.» р. могут служить распределения квадратов случайных величин, подчиняющихся Рэлея распределению и Максвелла распределению. В терминах «Х.-к.» р. с чётным числом степеней свободы выражается Пуассона распределение: Если количество слагаемых f суммы c2 неограниченно увеличивается, то согласно центральной предельной теореме распределение нормированного отношения сходится к стандартному нормальному распределению: где Следствием этого факта является другое предельное соотношение, удобное для вычисления Ff (x) при больших значениях f: Распределение Стьюдента - распределение получило свое название от псевдонима Student, которым английский ученый Госсет подписывал свои работы по статистике. Пусть -- независимые стандартные нормальные случайные величины. Распределением Стьюдента с степенями свободы называется распределениеследующей случайной величины: (46) Если вспомнить введенную формулой (44) случайную величину , то можно сказать, что отношение имеет распределение Стьюдента. Плотность этого распределения представляет собой симметричную функцию, задаваемую формулой По форме график функции напоминает график плотности стандартного нормального закона, но с более медленным убыванием ``хвостов''. При последовательность функций сходится к функции , которая есть плотность распределения . Чтобы понять, почему этот факт имеет место, следует обратить внимание на то, что по закону больших чисел знаменатель выражения (46) при стремится к Теорема Фишера для нормальных выборок В этом параграфе мы приводим теорему, впервые доказанную Р.А. Фишером в 1925 г. Она существенно облегчает статистический анализ независимых выборок из нормального распределения. Теорема Фишера. Пусть независимая выборка из распределения Тогда 1. выборочное среднее и выборочная дисперсия независимы; 2. имеет -распределение с степенью свободы.

Примечание: (1-p)=q это стандартное обозначение вероятности неудачи.

Определение

Биномиальное распределение — дискретное распределение вероятностей одной случайной величины   принимающей целочисленные значения   с вероятностями:

Данное распределение характеризуется двумя параметрами: целым числом   называемым числом испытаний, и вещественным числом     называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из   независимых испытаний, в каждом из которых может произойти "успех" с вероятностью   то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы   независимых слагаемых, имеющих распределение Бернулли.

Основные свойства

Характеристическая функция: 

Моменты:

Математическое ожидание: 

Дисперсия: 

Асимметрия:   при  распределение симметрично относительно центра 

Пример

Пусть     Оценим вероятность того, что число успехов будет отличаться от наиболее вероятного значения   не более чем на  . Заметим, что значение   очень мало, поэтому применение нормального приближения здесь довольно ненадежно.

Точная вероятность рассматриваемого события равна

Применим нормальное приближение с той расстановкой неравенств, которая дана выше (снизу строгое, сверху нестрогое):

О шибка приближения равна  .

Т еперь построим приближение, используя интервал с концами в полуцелых точках:

Ошибка приближения равна   — примерно в 5 раз меньше, чем в предыдущем подходе.

15. Показательное распределение.

Показательное распределение -   распределение вероятностей на действительной прямой с плотностью вероятностей f_ξ (х), равной при х ≥ 0 показательной функции αe^-αx, λ > 0 и при х < 0 — нулю. Вероятность того, что случайная величина X, имеющая П. р., примет значения, превосходящие некоторое произвольное число х, будет при этом равна e^αx

Говорят, что имеет показательное (экспоненциальное) распределение с параметром , и пишут: , если имеет следующую плотность распределения:

   

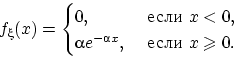
Функция распределения случайной величины непрерывна:

Генеральная совокупность и выборка.

Генеральная совокупность – совокупность элементов, удовлетворяющих неким заданным условиям; именуется также изучаемой совокупностью. Генеральная совокупность (Universe) - все множество объектов (субъектов) исследования, из которого выбираются (могут выбираться) объекты (субъекты) для обследования (опроса).

    ВЫБОРКА или выборочная совокупность (Sample) — это множество объектов (субъектов), отобранных специальным образом  для обследования (опроса). Любые данные, полученные на основании выборочного обследования (опроса), имеют вероятностный характер. На практике это означает, что в ходе исследования определяется не конкретное значение, а интервал, в котором определяемое значение находится.

Характеристики выборки:

- Качественная характеристика выборки – что именно мы выбираем и какие способы построения выборки мы для этого используем.

- Количественная характеристика выборки – сколько случаев выбираем, другими словами объём выборки.

Необходимость выборки:

- Объект исследования очень обширный. Например, потребители продукции глобальной компании – огромное количество территориально разбросанных рынков.

- Существует необходимость в сборе первичной информации.

Объём выборки — число случаев, включённых в выборочную совокупность.

Зависимые и независимые выборки.

При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми.

В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми.

Типы выборки.

Выборки делятся на два типа:

- вероятностные;

- не вероятностные;

     Репрезентативная выборка — выборочная совокупность, в которой основные характеристики совпадают с характеристиками генеральной совокупности. Только для этого типа выборки результаты обследования части единиц (объектов) можно распространять на всю генеральную совокупность. Необходимое условие для построения репрезентативной выборки — наличие информации о генеральной совокупности, т.е. либо полный список единиц (субъектов) генеральной совокупности, либо информация о структуре по характеристикам, существенно влияющим на отношение к предмету исследования.

17. Дискретный вариационный ряд, ранжирование, частота, частность.

Вариационным рядом (статистическим рядом) – называется последовательность вариант, записанных в порядке возрастания и соответствующих им весов. Вариационный ряд может быть дискретным (выборка значений дискретной случайной величины) и непрерывным (интервальным) (выборка значений непрерывной случайной величины). Дискретный вариационный ряд имеет вид: 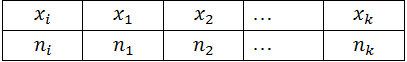Наблюдаемые значения случайной величины х1, х2, …, хk называются вариантами, а изменение этих значений называются варьированием. Выборка (выборочная совокупность) – совокупность наблюдений, отобранных случайным образом из генеральной совокупности. Число наблюдений в совокупности называется ее объемом. N – объем генеральной совокупности. n– объем выборки(сумма всех частот ряда). Частотой варианты хi называется число ni (i=1,…,k), показывающее, сколько раз эта варианта встречается в выборке. Частостью (относительной частотой, долей) варианты хi (i=1,…,k) называется отношение ее частоты ni к объему выборки n. wi=ni/n Ранжирование опытных данных - операция, заключающаяся в том, что результаты наблюдений над случайной величиной, т. е. наблюдаемые значения случайной величины, располагают в порядке неубывания. Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов хi с соответствующими им частотами или частностями.