25* Динамиканың негігі зандары

- Еркін нүктенің қозғаушы күш әсерінен алған үдеуі осы күш бағытында болып, мөлшері осы күш мөлшеріне пропорционал болады (14.1-сурет). Бұл заңның математикалық өрнегі төмендегідей жазылады:

F=mа (14.1)

Мұндағы Ғ - қозғаушы күш, m - нүктенің массасы, а - оның үдеуі. (14.1) түрінде берілген векторлық теңдеу нүкте динамикасының негізгі теңдеуі делінеді. (14.1)-ден көретініміз, белгілі күш әсерінде нүктенің алатын үдеуі тек күш мөлшеріне байланысты ғана болмастан, нүктенің массасына да байланысты екендігі.

Егер нүкте тек өзінің ауырлық күші ( G) әсерінде жерге еркін түсетін болса, Ғ= G, а=g болып, (14.1) өрнек

G=mg (14.2)

түріне келеді. Демек, нүктенің ауырлық күші мен массасы өзара (14.2) теңдікпен байланысты екен.

Егер нүктенің ауырлық күші белгілі болса, оның массасын (14.2) ге сәйкес

m=  (14.3)

формуладан табу мүмкіндігі туады.

Халықаралық бірліктер жүйесі (СИ) де масса бірлігі үшін кг, уақыт бірлігі үшін секунд (1с), ұзындық бірлігі үшін метр (1м) қабылданған. Онда күш бірлігі төмендегідей болады:

[F] = [m][a]=кг = Н (Ньютон).

Демек, массасы 1кг болатын нүктеге 1м/с² үдеу беретін күш Ньютон деп аталады.

26* Материялық нүкте қозғалысының дифференциалдық теңдеулері - Еркін нүкте   күшінің әсерінен қозғалыста болсын (14.4-сурет).Бұл жағдайда динамиканың негізгі теңдеуі (14.1) түрінде жазылады. (14.1) теңдеудегі   үдеу векторын   радиус - векторы арқылы өрнектейміз:

  . (14.7)

 

14.4 - сурет

(14.7) - ні (14.1)-ге қойсақ, онда

 (14.8)

келіп шығады. (14.8) теңдеуі еркін нүкте қозғалысының дифференциал теңдеуінің векторлық өрнегі. (14.8) векторлық өрнектің Декарт координата өстеріндегі проекциялары төмендегідей болады:

 (14.9)

Бұл өрнектерде   арқылы   күшінің координата өстеріндегі проекциялары белгіленген, x,y,z арқылы   радиус- вектордың проекциялары, яғни М нүктенің координаттары. (14.9) теңдеулер, қисық сызықты қозғалыстағы нүкте қозғалысының дифференциал теңдеулері координат әдісімен берілген делінеді. Егер нүктенің қозғалыс бағыты мен күш бағыты бір түзу бойымен болса, нүкте қозғалысы түзу сызықты болады. Бұл жағдайда нүктенің қозғалыс бағыты үшін О_х өсін алсақ, оның диффренциал теңдеуі төмендегідей жазылады:

 (14.10)

Егер нүктенің қозғалысы жазықтықта болса, онда (14.9) теңдеулердің алғашқы екеуі (қозғалыс О_хү жазықтығында) жазылады. (14.1) теңдеулердің табиғи координата өстеріндегі проекциялары төмендегідей болады (14.5-сурет):

( 14.11)

 

Кинематикадан бізге белгілі:

=d /dt,  ² / , a_b =0 (14.12)

 

(14.12) өрнекті (14.11) теңдеулер жүйесіне апарып қойсақ, онда

 

m , F_n =m ² / , F_b = 0 (14.13)

 

келіп шығады.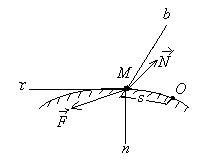

 

 

 

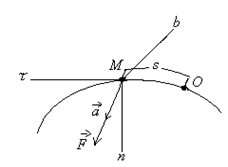
 14.5 - сурет 14.6 - сурет

 Нәтижеде табылған (14.13) теңдеулер, нүкте қозғалысы табиғи әдіспен берілген кездегі оның дифференциал теңдеулері болып есептелінеді.

Енді нүкте жылжымайтын жылтыр сызық үстінде қозғалып бара жатқан болсын (14.6-сурет). Санақ жүйесінің басын О деп, Мнүктенің қисық сызықты координатасын   деп қабылдаймыз. Қозғалмайтын жылтыр сызықтың нүктеге көрсететін әсерін реакция   күшімен ауыстырып, нүктені байланыстан ойша босатамыз.

Нәтижеде еріксіз нүкте динамикасының негізгі теңдеуі төмендегідей жазылады

, немесе

. (14.14)

Бұл теңдеуді Декарт координат өстеріне проекцияласақ, еріксіз нүкте қозғалысының дифференциал теңдеулерінің координат тәсілдеріндегі өрнегі келіп шығады:

, ,  (14.15)

(14.14) векторлық теңдеуді табиғи координат өстеріне проекциялаймыз. Онда

.

Қозғалмайтын сызық жылтыр болғандықтан   реакция күшінің жанамаға болған проекциясы нөлге тең, яғни 

Демек,

 (14.16)

(14.16) материялық нүктенің қозғалмайтын жылтыр сызық үстіндегі қозғалысының дифференциал теңдеулерінің табиғи тәсілде өрнектелуі.

Дербес жағдайда   күші жанама жазықтықта орналасса, онда Ғ_b=0 болып нормал реакция күші траекторияның бас нормалымен бағыттас болады.