21* Нүктенің күрделі қозғалысы - Нүктенің күрделі қозғалысы. Қатты дененің күрделі қозғалысы

Нүкте немесе қатты дене бірнеше қозғалысқа қатысса, онда бұл нүктенің немесе қатты дененің қозғалысын күрделі қозғалыс деп атайды.

Нүктенің немесе дененің жылжымалы координаттық системасына қатысты қозғалысын салыстырмалы қозғалыс деп атайды.

Нүктенің немесе дененің жылжымалы координаттық системасымен бірге қозғалмайтын координаттық системаға қатысты қозғалысын орын ауыстыру немесе тасымал қозғалыс деп атайды.

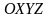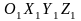М нүктесі координаттық системасына қатысты қозғалғанда ол координаттық система осы нүктемен бірге, қозғалмайтын координаттық системасына қатысты қозғалыста.

Салыстырмалы қозғалыстың жылдамдықта-рына, үдеулеріне, қозғалу заңын белгілейтін теңдеулерге төменгі 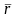индексі, ал тасымал қозғалыстың кинематикалық күйін сипаттайтын шамаларға е индексі беріледі. Салыстырмалы қозғалыстағы жылдамдық пен үдеу ретімен 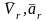деп, ал тасымал қозғалысындағы осы шамаларды 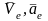деп белгілейді.

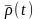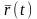нүктенің кординаттық системасындағы, ал нүктенің координаттық системасындағы қозғалуын береді.

нүктенің 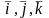бірлік векторлары координаттық система қозғалғанда бағыттарын өзгертуіне байланысты пайда болады. Осы вектордан уақытқа қатысты туынды анықталады:

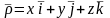
Өрнектің екі жағынан уақытқа қатысты бір туынды алсақ, ол былай өрнектеледі:

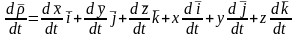
Өрнектің оң жағындағы бірінші жазылған үш қосынды векторының системасына қатысты өзгеруін сипаттайды, сондықтан бұл мүшелерді салыстырмалы туынды деп атайды.

Егер векторларының уақытқа қатысты туындыларын түрлендіргенде:

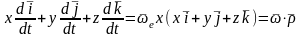
Сонда векторының абсолют туындысын былай жазуға болады:

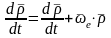
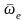мен 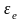жылжымалы координаттық системаның қозғалмайтын системаға қатысты айналмалы қозғалысының бұрыштық жылдамдығы мен бұрыштық үдеуі.

22* Жылдамдықтарды қосу туралы теорема - Жылдамдықтарды қосу туралы теорема

Теорема: нүктенің күрделі қозғалыстағы жылдамдығы оның салыстырмалы және тасымал жылдамдықтарының векторлық қосындысына тең: 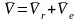, мұндағы 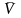- нүктенің күрделі қозғалысындағы жылдамдығы немесе абсолют жылдамдық деп атайды.

Радиус векторларының байланыстары:

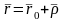
Нүктенің абсолют жылдамдығын уақытқа қатысты бірінші туындысы ретінде жазуға болады:

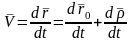
мұндағы ,

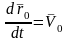сондықтан

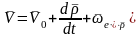
23* Үдеулерды қосу туралы теорема (Кориолис теоремасы). - Үдеулерді қосу туралы теорема

Теорема: Нүктенің күрделі қозғалыстағы үдеуі оның салыстырмалы, тасымал және бұрылу үдеулерінің векторлық қосындысына тең.

Бұл теорема былай өрнектеледі:

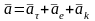
Мұндағы ретіменен нүктенің салыстырмалы, тасымал және бұрылу үдеулері, - нүктенің абсолют үдеуі.

24* Қатты дененің күрделі қозғалысы. - Нүкте немесе қатты дене бірнеше қозғалысқа қатысса, онда бұл нүктенің немесе қатты дененің қозғалысын күрделі қозғалыс деп атайды.

Нүктенің немесе дененің жылжымалы координаттық системасына қатысты қозғалысын салыстырмалы қозғалыс деп атайды.

Нүктенің немесе дененің жылжымалы координаттық системасымен бірге қозғалмайтын координаттық системаға қатысты қозғалысын орын ауыстыру немесе тасымал қозғалыс деп атайды.

М нүктесі координаттық системасына қатысты қозғалғанда ол координаттық система осы нүктемен бірге, қозғалмайтын координаттық системасына қатысты қозғалыста.

Салыстырмалы қозғалыстың жылдамдықта-рына, үдеулеріне, қозғалу заңын белгілейтін теңдеулерге төменгі индексі, ал тасымал қозғалыстың кинематикалық күйін сипаттайтын шамаларға е индексі беріледі. Салыстырмалы қозғалыстағы жылдамдық пен үдеу ретімен деп, ал тасымал қозғалысындағы осы шамаларды деп белгілейді.

нүктенің кординаттық системасындағы, ал нүктенің координаттық системасындағы қозғалуын береді.

нүктенің бірлік векторлары координаттық система қозғалғанда бағыттарын өзгертуіне байланысты пайда болады. Осы вектордан уақытқа қатысты туынды анықталады:

Өрнектің екі жағынан уақытқа қатысты бір туынды алсақ, ол былай өрнектеледі:

Өрнектің оң жағындағы бірінші жазылған үш қосынды векторының системасына қатысты өзгеруін сипаттайды, сондықтан бұл мүшелерді салыстырмалы туынды деп атайды.

Егер векторларының уақытқа қатысты туындыларын түрлендіргенде:

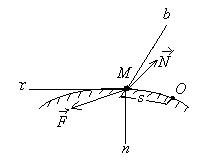
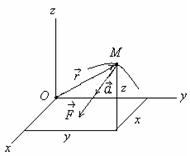
Сонда векторының абсолют туындысын былай жазуға болады:

мен жылжымалы координаттық системаның қозғалмайтын системаға қатысты айналмалы қозғалысының бұрыштық жылдамдығы мен бұрыштық үдеуі.