17* Қатты дененің жазық-параллель қозғалысы.
Қатты дененің қимасындағы нүктелер қозғалмайтын жазықтыққа параллель жылжитын болса, ол дененің қозғалуын жазықтыққа параллель қозғалыс деп атайды.
Қатты
дене
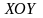жазықтығына
параллель қозғалатын болсын. Анықтама
бойынша дене қозғалғанда, оның қимасы
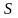жылжымайтын
жазықтығына
параллель қозғалады. Бұл шарт дене
║
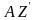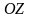осіне
байланысты айналғанда да
осімен
бірге ілгерілемелі қозғалғанда да
бұзылмайды, демек жазықтыққа параллель
қозғалысты осы қарапайым қозғалыстардан
құрастыруға болады.
Дене
жазықтыққа параллель қозғалғанда қимада
жатқан А нүктесімен ілгерілемелі және
сол нүктеге қатысты айналмалы қозғалыста
болады, сондықтан оның қозғалу заңын
былай жазуға болады:
,
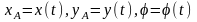мұндағы А таңдалып алынған S қимасында
жататын
нүкте. Бұдан кейінгі ілгерілемелі қозғалатын нүктені полюс деп атаймыз. Қимаға перпендикуляр әр остің бойындағы нүктелер дене жазықтыққа параллель қозғалғанда бірдей жылдамдықпен, бірдей үдеумен жылжиды.
В әріптерімен белгіленген қатты дененің нүктелері полюспен, яғни А-мен бірге ілгерілемелі жылжығанда да, полюске қатысты айналмалы қлзғалғанда да бірдей жылдамдықпен және бірдей үдеумен қозғалады.
18* Қатты дененің жазық-параллель қозғалысытағы нүктелеріның жылдамдығы
Жазықтыққа
параллель қозғалып жатқан қатты дененің
қимасын бөлек алып қарастырамыз.Полюсты
А деп белгілеп, оның қозғалуын
-
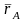радиус-векторымен анықтаймыз. Сонда
қимадағы кез-келген В нүктесінің
радиус-векторы
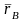полюстың
- радиус-векторымен мынадай байланыста
болады:
,
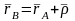мұндағы
.
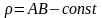В нүктесінің жылдамдығын табу үшін
өрнектің екі жағынан уақыт бойынша бір
туынды аламыз:
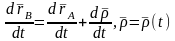
Бұл
өрнекте
,
,
-
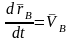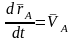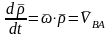
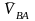В нүктесінің полюске қатысты айналмалы
қозғалысындағы жылдамдығы. S қимасындағы
В нүктесінің жылдамдығы былай анықталады:
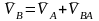
Сонымен, жазықтыққа параллель қозғалып жатқан қимадағы кез-келген нүктенің жылдамдығы полюспен бірге ілгерілемелі және полюске қатысты айналмалы қозғалыстағы нүктенің жылдамдықтарының векторлық қосындысына тең.
Егер жылдамдыққа паралель қозғалыстағы дененің қозғалу заңы берілсе, онда өрнектің оң жағындағы шамалар былай табылады:
,
,
,
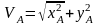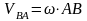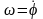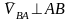
Сонан
соң В нүктесінің жылдамдығының шамасы
мына түрде жазылады:
^
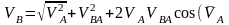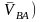
20* Қатты дененің жазық-параллель қозғалысытағы нүктелеріның үдеуі.
Жазықтыққа параллель қозғалатын қимадағы
нүктелердің үдеулерін анықтау
,
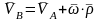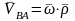
Бұл өрнекті уақытқа қатысты бір туынды аламыз:
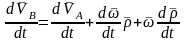
19* Жылдамдықтардың лездік центрі.
Лездік жылдамдықтар центрі
Қима жазықтыққа параллель қозғалғанда жылдамдығы нөлге тең қиманың нүктесін лездік жылдамдықтар центрі деп аталады.
Айналмалы қозғалыстың анықтамасы бойынша жылдамдығы нөлге тең нүкте, яғни қозғалмайтын нүкте, айналу осінде жатады, демек лездік жылдамдықтар центрі де солай орналасады. Сонда қимадағы нүктелердің барлығы лездік жылдамдықтар центріне қатысты айналмалы қозғалыста деп алуға болады.
Лездік
жылдамдықтар центрін Р деп белгілеп,
оны полюс ретінде қолдансақ, В нүктесінің
жылдамдығын өрнек бойынша мына түрде
жазуға болады:
,
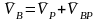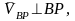
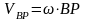
мұнда
анықтама бойынша
,
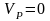сондықтан
,
,
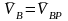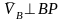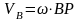
А
нүктесінің жылдамдығы мына түрде
жазылады:
,
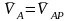
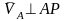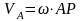
Бұл
теңдеулерден
;
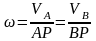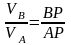
Жоғарыдағы өрнектерден мынадай нәтижелер байқауға болады:
Қимадағы кез-келген нүктенің жылдамдығы лездік жылдамдықтар центріне дейінгі кесіндіге перпендикуляр бағытталады. Жылдамдықтар центріне дейінгі кесіндінің бұрыштық жылдамдыққа көбейтіндісі ретінде анықталады.
Бұрыштық жылдамдық қимадағы кез-келген нүктенің жылдамдығының лездік жылдамдықтар центріне дейінгі кесіндіге қатынасы ретінде анықталады.
Кез-келген екі нүктенің жылдамдықтарының қатынасы сол нүктелерден лездік жылдамдықтар центріне дейінгі кесінділердің қатынасына тең.
Лездік жылдамдықтар центрі қимадағы кез-келген екі нүктеден жылдамдықтарға өткізілген перпендикулярлардың түйісу нүктесінде орналасады.
Егер жылдамдықтардың шамалары өзара тең болмай бағыттары параллель түзулерде жатса, онда лездік жылдамдықтар центрі нүктелерден жылдамдықтарға түсірілген перпендикуляр және олардың ұшынан жүргізілген түзу түйіскен нүктеде орналасады. Егер бір дене жазықтыққа параллель қозғалғанда ол екінші дененің немесе жазықтықтың бетімен сырғымай жанасатын болса, онда лездік жылдамдықтар центрі жанасу нүктесінде орналасады.
Егер нүктелердің жылдамдықтары өзара тең және параллель болса, онда лездік жылдамдықтар центрі шексіз алыста орналасады да, дененің қозғалуы лездік ілгерілемелі қозғалыс деп аталады.
Нүктелердің жылдамдықтары параллель түзулерде орналасқан жағдайда дененің бұрыштық жылдамдығы былай анықталады:
,
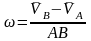Мұнда жылдамдықтар АВ кесіндісіне перпендикуляр оське проекцияланып әрқайсысы өз таңбасымен жазылады.
Уақыттың өзгеруіне қарай лездік жылдамдықтар центрінің орны да ауысып отырады. Олардың жылжымайтын жазықтықтағы геометриялық орындары қозғалмайтын, ал жылжымалы жазықтықтағы геометриялық орындары жылжымалы центронда деп аталады.