15* Қатты дененің ілгермелі қозғалысы

- Дененің кез-келген екі нүктесін жалғайтын дене қозғалғанда өзіне-өзі параллель болатын болса, онда дененің қозғалуы ілгерілемелі деп аталады.

Дене ілгерілемелі қозғалыста болсын. Анықтама бойынша кез-келген екі нүктелерден өткізілген АВ түзуі дене ілгерілемелі қозғалғанда ұдайы өзіне-өзі параллель жылжиды, сондықтан 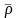векторының бағыты да, шамасы да өщгермейді, яғни 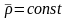. Нүктелердің қозғалуын 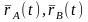- радиус-векторымен анықтайтын болсақ, онда:

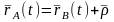
Анықтама бойынша:

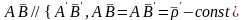
Нүктелердің жылдамдықтарының арасындағы тәуелділігін табу үшін, өрнектің екі жағынан уақытқа қатысты бір туынды аламыз:

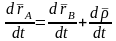, мұндағы

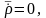
өйткені

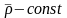
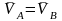
Енді жоғарыдағы теңдеуден уақытқа қатысты бір туынды алатын болсақ, онда , немесе

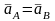
Ілгерілемелі қозғалыстағы дененің барлық нүктелерінің жылдамдықтары, үдеулері өзара тең болады да нүктелері бірдей траекториялармен жылжиды. Ол траекториялар қисық сызықты да, түзу сызықты да болады.

Ілгерілемелі қозғалыстағы дененің қозғалуын зерттеу үшін сол дененің кез-келген жалғыз нүктесін алып зерттеуге болады. Ілгерілемелі қозғалыстағы дененің еркіндік дәрежесі еркін жалғыз нүктенің еркіндік дәрежесіне, яғни үшке тең, сондықтан ілгерілемелі қозғалатын дененің қозғалу заңын былай жазуға болады:

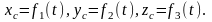
16* Қатты дененің өске қатысты айналмалы қозғалысы.

Бұрыштық жылдамдық пен бұрыштық үдеу. Сызықтық жылдамдық пен бұрыштық үдеу- Егер дене қозғалып тұрған кезінде ондағы екі нүкте жылжымайтын болса, онда бұл қозғалыс айналмалы қозғалыс делінеді (9.2 сурет).

Жылжымайтын О және А нүктелерден жүргізілген түзу дененің айналу өсі деп аталады. Дененің айналмалы қозғалысын зерттеу үшін жылжымайтын Р₀ және денемен бірге қозғалатын Р жазықтықты аламыз.

Олар арасындағы бұрыш

 болсын.

Дене қозғалғанда, Р₀ және Р жазықтықтар арасындағы бұрыш өзгеріп барады. Нәтижеде осы бұрыш уақыттың функциясы болады:

 (9.5)

 

(9.5) дененің бұрылу немесе айналу бұрышы делінеді және ол радианмен 9.2 сурет

өлшенеді. (9.5) теңдеуі қатты дененің

жылжымайтын өсь төңірегіндегі 9.2 сурет

айналмалы қозғалысының заңы немесе айналу қозғалысының теңдеуі делінеді.

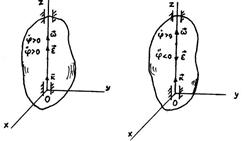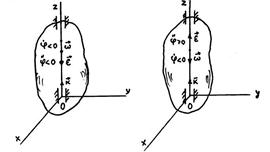А йталық, t=t₀ де дененің бұрылу б ұрышы  , ал t=t₁ де   болсын. Бұл жағдайда уақыт өзгеруі  , бұрылу бұрышының өзгеруі   болады.

Бұрылу бұрышының өзгеруінің уақыт өзгеруіне қатынасы дененің орташа бұрыштық жылдамдығы делінеді және   мен белгіленеді.

 (9.6)

Дененің кез-келген шақтағы бұрыштық жылдамдығын табу үшін   нөлгеұмтылғанда (9.6)-өрнектен шек аламыз, яғни

=

немесе

ω= =  (9.7)

Демек, дененің бұрыштық жылдамдығы оның бұрылу бұрышынан уақыт бойынша алынған бірінші туындыға тең. Оның өлшем бірлігі рад/с немесе 1/с-тен тұрады. Дененің бұрыштық жылдамдығы оның бұрылу бұрышының қаншалықты жылдам өзгеруін және өзгеру бағыты қандай екенін анықтайды.

Сондықтан дененің бұрыштық жылдамдығын вектор түрінде өрнектейді. Осы векторды дене айналу өсінің кезкелген нүктесіне қоямыз және бағытын сондай таңдаймыз, оның төбесінен қарағанда дене әрқашан сағат тіліне қарсы бағытта айналсын (9.3 сурет).

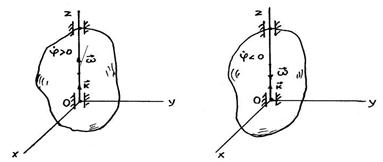
а ә

9.3 сурет

Oz өсті дененің айналу өсі ретінде қабылдап алсақ, оның бұрыштық жылдамдығының векторы былай жазылады:

 (9.8)

Мұнда   оz өсінің бірлік векторы.

Жалпы жағдайда дененің бұрыштық жылдамдығы уақыт өтуімен өзгереді. Егер t=t₀ болғанда бұрыштық жылдамдық  , ал t=t₁де   болсын. Бұрыштық жылдамдық өзгеруінің ( ) уақыт өзгеруіне ( ) қатынасы дененің орташа үдеуі деп аталады:

 . (9.9)

Мұндағы  -ні нөлге ұмтылтырып, шекке өтсек:   ,

немесе   (9.10)

(9.10) - өрнетктен көретініміз, дененің бұрыштық үдеуі оның бұрыштық жылдамдығынан уақыт бойынша бірінші немесе бұрылу бұрышынан алынған екінші туындыға тең екен.

Дененің бұрыштық үдеуінің векторын  айналу өсі бойынша бейнелеу мүмкін (2.4-сурет):

 

 

 

 

 

  а                                              ә                                     б                                     в

9.4 сурет

 

= = ,

немесе   . (9.11)

Дене бұрыштық үдеуінің өлшем бірлігі рад/с² немесе 1/с² болады. Дененің айналмалы қозғалысының дербес жағдайлары төмендегілерден тұрады:

Егер бұрыштық жылдамдық ( ) тұрақты болса,

Бұл жағдайда  .

Бұдан   (9.12)

келіп шығады.

(9.12) теңдеу дененің бір қалыпты айналмалы қозғалыс заңын өрнектейді. Егер   болса,

φ= ωt , ω=   (9.13)

болады.

Техникалық есептерді шешкен кезде көбінесе дененің 1 минуттағы айналу саны n берілген болады. Бұл жағдайда  ,  болып, (2.13) тен

ω= =  (2.14)

табамыз.

Кейбір мәселелерде кезкелген t₁ уақыттағы айналу санын табу талап етіледі. Бұл жағдайда айналу саны N-мен белгіленіп, ол төмендегі формула көмегінде анықталады:

φ=2πN,   (2.15)

2. Егер дененің бұрыштық үдеуі   тұрақты болса, дене қозғалысы бір қалыпты айнымалы қозғалыстан тұрады. Бұл жағдайда:

.

Бұдан  ,   (9.16)

келіп шығады.

(9.16) нің екінші теңдеуі дененің бір қалыпты айнымалы қозғалыс заңын өрнектейді. Егер қозғалыс бір қалыпты үдемелі болса, есепті шешуде   алдындағы таңба оң, бір қалыпты кемімелі болса,   алдындағы таңба теріс деп алынады (9.4 - сурет, ә,в).

Дене қозғалысы бір қалыпты үдемелі болғанда бұрыштық жылдамдық және бұрыштық үдеулердің таңбалары бірдей болады (9.4 - сурет, а,б).