12* Нүктенің әр түрлі берілу әдістегі жылдамдығы Нүктенің жылдамдығы

Нүктенің қозғалысы оның заңына байланысты түрлі бағытта, түрлі шапшаңдықпен өтеді. Қозғалу шапшаңдығын және бағытын сипаттайтын векторлық шаманы жылдамдық деп атайды.

1. Қозғалыс векторлық әдіспен берілген нүктенің жылдамдығы

М нүктесінің қозғалуы векторлық әдіспен берілсе: r=r(t). Келесі t₁ мерзімде нүкте М₁- де r₁ радиус-векторымен беріледі. Сонда радиус-вектор Δt=t₁-t уақытында мынадай өсімшесін алады: Δr=r₁-r=r(t+Δt)-r(t).

Орын ауыстыру векторының Δr сәйкес уақыт өсімшесіне Δt қатсынасы нүктенің орташа жылдамдығы деп аталады: V_орт= Δr/ Δt. Орташа жылдамдық орын ауыстыру векторына бағыттас. Ол Δr-дің уақыт бірлігінде өзгеруін сипаттайды. Δt мерзімі аз болған сайын Δr траекторияға жақындайды. Нүктенің t мезеттегі жылдамдығы V нүктенің лездік жылдамдығы деп аталады.

Егер нүкте түзу сызықтық қозғалыста болса, онда лездік жылдамдықта, орташа жылдамдықта нүктеден түзу бойымен бағытталады. Бұл жағдайда жылдамдықтың шамасы, уақыт өзгеруіне қарай, өзгеріп отырады. егер нүкет қисық сызықтық қозғалыста болса, онда лездік жылдамдықтың бағыты да, шамасы да айнымалы болады.

2. Қозғалысы координаттық әдіспен берілген нүктенің жылдамдығы.

М нүктесінің қозғалысы координаттық әдіспен берілсе: x=x(t), y=y(t), z=z(t). x,y,z радиус-вектордың координаттық остердегі проекциялары болғандықтан: r=xi+yj+zk

V=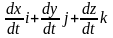

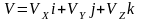; мұндағы 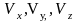- лездік жылдамдықтардың остердегі проекциялары.

3. Қозғалысы табиғи әдіспен берілген нүктенің жылдамдығы.

М нүктесінің қозғалуы табиғи әдіспен берілсе: S=S(t), V_орт= Δ S / Δt.

13* Нүктенің векторлық және координаталық берілу әдістегі үдеуілері- Нүктенің үдеуі

Төменде орын үнемдеу мақсатта лездік жылдамдықты – жылдамдық деп атаймыз.жылдамдық векторының өзгеру шапшаңдығын сипаттайтын векторлық шаманы үдеу деп атайды.бір қалыпты түзу сызықтық қозғалыста жылдамдықтың шамасы да, бағыты да өзгермейді, сондықтан тек осы қозғалыста үдеу нольге тең.

1. Қозғалысы векторлық әдіспен берілген нүктенің үдеуі.

М нүктесінің қозғалуы векторлық әдіспен берілсе, Δt уақыт арасында нүктенің жылдамдығы ΔV өсімшесін алады: Δt=t₁-t, ΔV = V₁- V₂. Жылдамдықтың өсімшесінің уақыт өсімшесіне қатынасы а_орт= Δ V / Δt – орташа үдеу деп аталады. Орташа үдеу а_орт жылдамдықтың өсімшесімен бағытталады да соның уақыт өсімшесінің арасындағы өзгеру шапшаңдығын жуық шамамен сипаттайды. Жылдамдықтың өзгеруін толық сипаттайтын вектор Δ t→0 болғандағы орташа үдеудің шегіне тең:

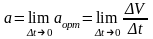; бұл векторлық шама лездік үдеу деп аталады.

Туындының анықтамасы бойынша өрнек былай көшіріледі:

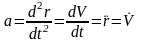
Нүктенің үдеуі радиус-вектордан уақыт бойынша алынған екінші, немесе жылдамдықтан уақыт бойынша алынған бірінші туындыға тең.

2. Қозғалысы координаттық тәсілмен берілген нүктенің үдеуі.

М нүктесінің қозғалысы координаттық тәсілмен берілсін: x=x(t), y=y(t), z=z(t).

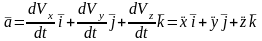
Үдеу векторының проекцияларын қолданып 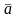шамасын табамыз:

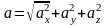
14* Нүктенің табиғи берілу әдістегі үдеуі.

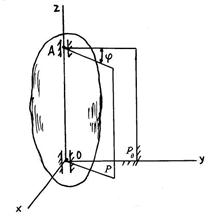
Қозғалысы табиғи әдіспен берілген нүктенің үдеуі.

М нүктесінің қозғалуы табиғи әдіспен берілсе: S=S(t). Нүктенің жылдамдығы жанама бойымен нүктенің қозғалу бағытына қарай бағытталады. М нүктесінің үдеуін анықтауда табиғи үшжақтық остерді қолданамыз. Бұл остердің бағыттары бірлік векторлармен беріледі: 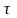- жанама, n – нормаль, в – бинормаль остері М нүктесінен аттас бірлік векторлар бойымен бағытталады да олардың құрастырып тұрған жазықтықтар жанасушы, түзулеуші, нормаль жазықтықтар деп аталады.

М нүктесі траектория бойымен жылжығанда бұл остер нүктемен бірге жылжиды. 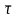бірлік векторы М нүктесінен траекторияға жанасып өтеді, ал қалған бірлік векторлар -ға перпендикуляр бағытталады. М нүктесі қозғалғанда векторының бағыты қалай өзгеретінін анықтаймыз. Δt уақыт арасында нүкте М-нен М₁ орнына ауысады да жанама бірлік векторы Δ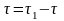 өсімшесіне алады. Сол арада доғалық координата да өзгеріп ΔS=S₁- S өсімшесін алады. Δ - дың ΔS-ке қатынасы Δ векторының М нүктесіне қатысты айналуын сипаттайды. Бұл векторлық шама орташа қисықтық деп аталады. ММ₁ доғасының орташа қисықтығы

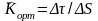
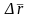бағытына параллель жүргізіледі. М₁ нүктесі М – ге ұмтылғанда 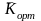шегі: 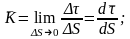траекторияның М нүктесіндегі қисықтығы деп аталады.

Қисықтық векторы нормаль бірлік вектор бойымен бағытталады, өйткені және Δ -дан құрап тұрған үшбұрышта мынадай қатынастар орындалады: 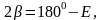егер 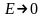болса, онда

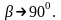
Математикалық анализде қисықтық векторының шамасы: 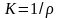; мұндағы 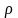- қисықтық радиусы. Осы өрнекті қолданып қисықтық векторын мына түрде өрнектейміз:

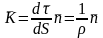
Шеңбердің қисықтық радиусы шеңбердің радиусына, ал түзу түзу сызықтың қисықтық радиусы 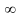- ке тең. Енді осыдан нүктенің үдеуін анықтаймыз. Жылдамдықты бірлік векторды пайдаланып, былай жазамыз: 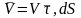>0, мұндағы V – жылдамдықтың шамасы, - жанама бірлік вектор.

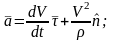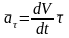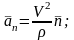бұл өрнектің бірінші қосындысы жылдамдықтың шамасының өзгеруін сипаттайды да нүктеден траекторияға жүргізілген жанама бойымен бағытталады. Оны жанама үдеу деп атайды, ол мына түрде жазалады: , ал екінші қосындысы жылдамдықтың бағытының өзгеруін сипаттайды да нүктенің траекторияның ойыс жағына қарай нормаль бірлік векторының бойымен бағытталады, оны нормаль үдеу деп атайды. Нүктенің үдеуі жанама үдеу мен нормаль үдеуінің векторлық қосындысына тең:

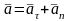
Нүктенің үдеуінің шамасы мен бағыты былай анықталады: 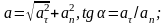мұндағы 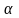- үдеу векторы мен нормаль бірлік векторының арасындағы бұрыш.