10* Ауырлық центрі. Қарапайым біртекті денелердің ауырлық центрлері

Жер бетіне жақын болған қатты дененің әрбір бөлігіне жер центріне қарай бағытталған ауырлық күші әсер етеді. Қарастырылып жатқан дене өлшемдері жер өлшемдеріне қатысты өте кіші болғандықтан әсер ететін ауырлық күштерін параллель деп қарастыру мүмкін. Демек, параллель күштер центрі дененің ауырлық центрінен тұрады. Сонымен, дененің ауырлық центрі (7.5) формуладан анықталады.Дене бөліктеріне әсер ететін ауырлық күштерінің тең

әсерлісін G десек,

Нәтижеде (7.5) төмендегідей жазылады:

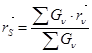 (7.6)

7.3 сурет

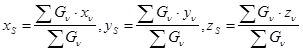. (7.7)

Қарапайым біртекті денелердің ауырлық центрлері

Бір текті дененің салмағы оның көлеміне пропорционал болсын. Бұл жағдайда

 (7.8)

мұндағы  - бір бірлік көлемнің салмағы,  - дененің V - бөлігінің көлемі.

 (7.8) ді (7.7) ге қойсақ:

 

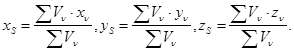 (7.9)

Координаттары (7.9) формуламен анықталатын нүкте, дене көлемінің ауырлық центрі делінеді (7.4 сурет)

Дене ауданының ауырлық центрін анықтау үшін одан S_V ауданды бөліп аламыз. (7.5 сурет). Бұл аудан салмағы:

 (7.10)

М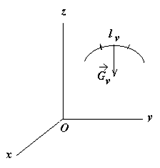 ұнда  - бір бірлік аудан салмағы; SV- дененің V- бөлігінің ауданы.

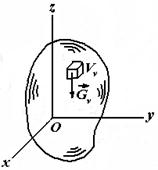
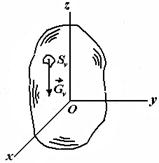
7.4 сурет 7.5 сурет 7.6 сурет

 

(7.10) ды (7.7) ге қойсақ:

 

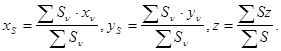 (7.11)

(7.11) дене ауданы ауырлық центрінің координаттарын анықтайтын формула.

Қисық сызықты доғаның ауырлық центрінің координаттарын табу үшін, одан  - доғаны бөліп аламыз. Бұл доғаның салмағы:

 (7.12)

Мұнда р- ұзындығы бір бірлікті беретін доғаның салмағы;   - дененің V- бөлігінің ұзындығы (7.6 сурет).

(7.12) ні (7.7) ге қойсақ:

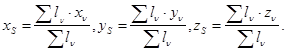 (7.13)

(7.13) тен қисық сызықты доғаның ауырлық центрінің координаттары анықталады.

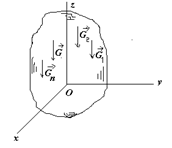
9* Параллель күштер центрі.

Кеңістікте бір жаққа қарай бағытталған параллель   күштер дененің   нүктелеріне қойылған болсын (7.2 сурет). Күштер қойылған нүктелердің радиус векторларын сәйкес   деп белгілейік. Жоғардағы тақырыпқа негізделіп, әуелі   және   күштерін қоссақ:

 

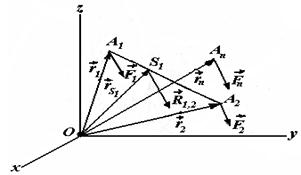
7.2 сурет

S₁ нүктенің радиус-векторын   десек, онда 

Бұл өрнектен 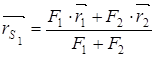  келіп шығады.

Әрі қарай қосуды жалғастырсақ:

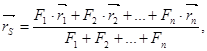
немесе

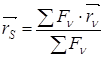 (7.5)

болады.

(7.5) формула көмегімен анықталатын S нүкте параллель болған күштер центрі (орталығы) делінеді.

11* Нүкте қозғалысының берілу әдістері

Әдетте нүкте қозғалысын төмендегі үш әдістердің бірімен береді:

1. Векторлық әдіс

2. Координаттық әдіс

3. Табиғи әдіс

1. Векторлық әдісте нүктенің әр сәтте кеңістіктегі орнын жылжымайтын нүктеден жүргізілген радиус-вектор анықтайды.

М әрпімен белгіленген нүкте кеңістікте жылжуына қарай ОМ радиус-векторының шамасы мен бағыты өзгеріп отырады: r=r(t). Бұл радиус вектордың шамасы М нүктесі жылжымайтын О нүктесінен қаншалықты ұзаққа қозғалып кеткенін, ал оның бағыты нүктенің қайсы бағытта жылжығанын белгілейді. Жоғарыдағы өрнек М нүктесінің қозғалу заңы, немесе векторлық қозғалу иеңдеуі деп аталады.

2. Координаттық әдісте нүктенің әр кеңістіктегі орнын оның координаталары анықтайды. М нүктесі OXYZ кеңістігінде қозғалуына қарай оның координаталары да өзгеріп отырады: x=x(t), y=y(t), z=z(t).

Бұл теңдеулер уақыттың өзгеруіне қарай нүктенің кеңістіктегі орнын анықтайды, яғни нүктенің қозғалуын координаттық әдіспен береді. Жоғарыдағы теңдеулерді координаттық әдіспен берілген нүктенің қозғалу заңы деп атайды.

Егер нүкте қозғалғанда OXY жазықтығында орналасса, онда теңдеулер мына түрде жазылады: x=x(t), y=y(t). Бұл жағдайда нүктенің қозғалуын полярлық координаттармен анықтауға болады: r=r(t), .

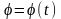мұндағы, r – полярлық радиус;

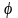- полярлық бұрыш,  - нүктенің цилиндрлік координаталары.

3. Табиғи әдісте нүктенің әр сәтте кеңістіктегі немесе жазықтықтағы орнын доғалық координатамен траекторияның бойынан анықтайды. Бұл әдісті нүктенің траекториясы белгілі болған жағдайда қолданады. Траекториядан санақ нүктесін таңдап алып, одан траекториямен қозғалу бағытының оң және кері жолын белгілейді де, нүктенің әр сәттегі орнын доғалық координатамен анықтайды. Доғалық координата S уақыттың өзгеруіне қарай өзгереді де, нүктенің траектория бойымен қозғалуын кез-келген мерзімде береді: S=S(t).