*3 Бiр нүктеге жинақталған күштер жүйесiнiң тепе-теңдiк шарты

 Қатты дене алғашқы кезде тыныштықта немесе бiр қалыпты түзу сызықтық қозғалыста болсын. Дененiң бұл күйiн тепе-теңдiк деп атаймыз.Дене бұл күйiнде қалу үшiн жаңадан түсiрiлген күштер тек теңгерiлген күштер болуы тиiстi. Теңгерiлген күштер жүйесiнiң тең әсер етушi күшi нольге тең болады, сондықтан бiр нүктеге жинақталған күштер системасы тепе-теңдiкте болу шарты былай жазылады:

 (2.8)

Бiр нүктеге жинақталған күштер жүйесi тепе-теңдiкте болу үшiн күштер көпбұрышы тұйық болуы қажеттi де жеткiлiктi.

Бұл тепе-теңдiк шартты бiз бұдан былай бiр нүктеге жинақталған күштер жүйесiнiң векторлық тепе-теңдiк шарты деп атаймыз. Кейде бұл шартты геометриялық шарт деп атайды. Егер бұл шарт орындалса, онда күштер көпбұрышының тұйықтаушы қабырғасы, яғни   нольге тең болады, сондықтан соңғы бағытталған күштiң соңғы нүктесi бiрiншi күштiң түсiп тұрған нүктесiне дәл орналасып қалады.

Кеңiстiктегi бiр нүктеге жинақталған күштер жүйесiнiң аналитикалық тепе-теңдiк шарты мына өрнектермен берiледi:

,  ,   (2.9)

Кеңiстiктегi бiр нүктеге жинақталған күштер жүйесi тепе-теңдiкте болу үшiн тiкбұрышты координаттық жүйенiң әр өсiне түсiрiлген барлық күштердiң проекцияларының қосындысы нольге тең болуы қажеттi де жеткiлiктi.

Егер бiр нүктеде жинақталған күштер жүйесi ОХУ жазықтығында орналасқан болса, онда аналитикалық тепе-теңдiк шарт былай жазылады

,  , (2.10)

 

өйткенi  -дiң ОZ өсiне проекциясы бұл жағдайда ұдайы нольге тең. Сонымен бұл шарттың анықтамасын былай жазуға болады:

"Жазықтықта бiр нүктеге жинақталған күштер жүйесi тепе-теңдiкте болу үшiн тiкбұрышты координаттық жүйенiң әрбiр өсiне түсiрiлген барлық күштердiң проекцияларының қосындысы нольге тең болуы қажеттi де жеткiлiктi".

7* . Жазықтыққа кез келген бағыттағы күштер системасының аналитикалық тепе теңдік шарттары

Кез-келген бағыттағы күштер системасы тепе-теңдікте болуы үшін системаның бас векторы және бас моменті нөлге тең болуы қажет, яғни

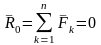
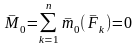
Егер системаның бас векторы мен бас моменті нөлге тең болса онда күштер системасы нөлге эквивалентті болғаны;

Егер күштер системасының бас векторы мен бас моменті бірдей нөлге тең болмаса онда система қос күшке келтіріледі.

6* Кез-келген бағыттағы күштер системасы ның тепе-теңдік шарты

Кез-келген бағыттағы күштер системасы тепе-теңдікте болуы үшін системаның бас векторы және бас моменті нөлге тең болуы қажет, яғни

Егер системаның бас векторы мен бас моменті нөлге тең болса онда күштер системасы нөлге эквивалентті болғаны;

Егер күштер системасының бас векторы мен бас моменті бірдей нөлге тең болмаса онда система қос күшке келтіріледі.

8* Айналу үйкелісі және домалау үйкелісі. Домалау үйкелісі. Айналу үйкелісі.

Бір дененің екінші дененің бетімен домалауына қарсы әсерді домалау үйкелісі деп атайды. Горизонталь кедір-бұдыр жазықтықпен салмағы Р-ға, радиусы R-ге тең қатты материалдан жасалған цилиндр К нүктесімен жанасып, F күшінің әсерінен жанасу нүктесіне қатысты сырғамай домалауға бейімделген.

Цилиндрге түсіп тұрған oxy жазықтығында кез-келген бағыттағы күштер системасының тепе-теңдік теңдеулерін анықтаймыз:

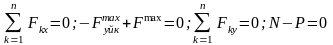
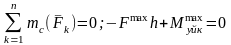Бұл теңдеулерден

;

;

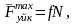
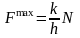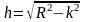
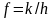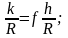
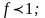
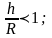
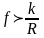
Сондықтан домалау үйкелісі сырғану үйкелісіне қарағанда кем кедергі етеді.

Техникада сырғанау үйкелісін домалау үйкелісіне алмастыруға болады. Цилиндрдің сырғанау және домалау шарттарын анықтаймыз.

Егер цилиндр тепе-теңдікте болса, онда ;

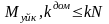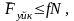
Осы шарт бұзылғанда цилиндр жылжи бастайды. Егер мына шарт орындалса цилиндр сырғымай домалайды:

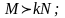
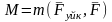
Цилиндр домаламай сырғу үшін мына шарт орындалуы қажет: ; 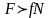. Егер мына шарт орындалса, онда цилиндр әрі домалап, әрі сырғып, жылжиды:

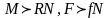
Бірақ 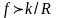болғандықтан, цилиндр тыныштықта алдымен домалай шығады да сонан соң сырғи бастайды.

Егер білік қуыс цилиндрлік тірек ішінде айналса, онда оған айналу үйкелісі кедергі береді. Айналу үйкелісінің моменті мына өрнекпен анықталады:

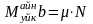
бұл жерде 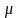-айналу үйкеліс коэффициенті; 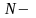жанасу сызығына жайылып түскен нормаль реакция.

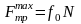
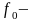тыныштық үйкеліс коэффициенті;

нормаль реакция

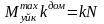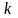; - домалау үйкеліс коэффициенті;

нормаль реакция

шектік домалау үйкеліс моменті;

- метрмен өлшенеді.

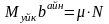-айналу үйкеліс коэффициенті;

нормаль реакция (жанасу сызығына жайылып түсіп тұрған нормаль реакция)

Күштерді 0 нүктесіне келтіреміз, сонда байланыстардың реакцияларынан өзге денеге бас вектор мен басмомент әсер етеді.

Бас моментті, моменті М₀-ге тең қос күшке түрлендіріп, денеге түсіп тұрған жазықтықта кез-келген бағыттағы күштер системасының, тепе-теңдік теңдеулерін анықтаймыз:

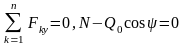
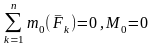. Соңғы теңдеу бойынша тепе-теңдіктегі дене келтіру нүктесіне қатысты айналмайды.

Екінші теңдеуден нормаль реакциясының шамасы анықталады: .

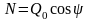Дене тепе-теңдікте болған кезде мына теңсіздік орындалады:

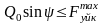
Сонымен денені жылжытуға бейімделген күштің кедергі етуші бетке жүргізілген нормальмен жасайтын бұрышы 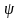үйкеліс бұрышынан кем болса дене тепе-теңдікте болады. Жылжытуға бейімделген күш кеңістікте де бағытталуы мүмкін, сондықтан тыныштық аумағы үйкеліс конусымен қамтылады.

Егер жанасу беттерінің кедергі жасау қабулеті біркелкі болса, онда үйкеліс конусы дөңгелек конус, ал біркелкі болмаса онда конустың табаны басқа бір тұйық фигура болады.

Күш конус бетінен тайғаг замат дене жылжи бастайды, конус ішінде не оның бетінде орналасса, онда күштің шамасы қандай болғанда да дене тепе-теңдікте болады. 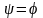болғанда үйкеліс конусының бетіне орналасады да дене шектік тыныштық күйін сақтап тұрады.