• 60. Динамиканың жалпы теңдеуі.

20.1 Динамиканың жалпы теңдеуі

 

Динамиканың жалпы теңдеуін келтіріп шығару үшін идеал және босатпайтын байланыстағы механикалық жүйе нүктелері үшін Даламбер принципін жазамыз:

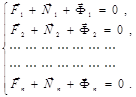 (20.1)

Жүйе нүктелеріне мүмкін болатын көшулер беріп (20.1) теңдеулерді сәйкес   терге скаляр көбейтіп, алынған өрнектерді мүшелеп қоссақ,

келіп шығады. Жүйе идеал байланыста болғандықтан

.

Сонымен,

 (20.2)

өрнекке ие боламыз.

(20.2) теңдеу аналитикалық тәсілде Декарт координат өстеріндегі проекциялары арқылы төмендегідей жазылады:

 (20.3)

(20.2) немесе (20.3) динамиканың жалпы теңдеуі делінеді және келесі теоремамен баяндалады:

Идеал және босатпайтын байланыстар қойылған механикалық жүйеге әсер ететін актив күштердің және инерция күштерінің әр қандай мүмкін болатын көшудегі элементтер жұмыстарының қосындысы нөлге тең.

Динамиканың жалпы теңдеуі Даламбер және Лагранж принциптерін бірге қарастырудан келіп шыққандығы себепті, (20.2) Даламбер- Лагранж теңдеуі деп те аталады.

59. Условие равновесия в обобщенных координатах

Согласно принципу виртуальных перемещений, условие     является необходимым и достаточным для равновесия системы с идеальными и стационарными связями. Переходя к обобщенным координатам, находим     Þ         .

 

Пусть связи, наложенные на систему, являются голономными. В силу независимости вариаций обобщенных координат равенство нулю возможно только в том случае, когда все коэффициенты при вариациях обобщенных координат равны нулю. 

 

Для равновесия механической системы с идеальными, стационарными и голономными связями необходимо и достаточно, чтобы все обобщенные силы были равны нулю

 

Для консервативных механических систем необходимым и достаточным условием равновесия является система  равенств: