58. Жалпыланған координаттар және жалпыланған күштер.
19.2. Жалпыланған координаттар. Жүйенің еркіндік дәрежесі.
Еріксіз механикалық жүйе нүктелерінің көшуі еркін болмастан, қандайда бір себеппен шегараланатыны белгілі. Бұл жүйе нүктелерінің барлық координаттары еркін түрде өзгермейтінін көрсетеді. Ал еріксіз координаталар байланыс теңдеулерінен табылады.
Айталық,
жүйе 
нүктелерден
құралған болып, оған s голономды
байланыс қойылған:
Демек, жүйе нүктелерінің 3n координаттары арасында s байланыс бар, яғни s координат еріксіз. Ал, жүйе нүктелерінің еркін координаттар саны k=3n-s координат арқылы анықталады.
Голономды байланыста болған жүйенің бірден-бір орнын анықтайтын өзара тәуелді болмаған параметрлер саны системаның еркіндік дәрежесі деп аталады.
Мысалы,
19.1-суретте көрсетілген кривошип-шатунды
механизмді алатын болсақ, оның кез-келген
уақытта алатын орнын 
арқылы
анықтауға болады. Егер механизмнің
орнын x2 арқылы
анықтайтын болсақ, онда x3және y2 лерді
(19.5) теңдеулер жүйесінен табуға болады.
Механизмнің кез-келген уақытта алатын
орнын анықтау үшін OAкривошиптің
айналу
бұрышын
алуға да болады. Демек, бұл механизмнің
еркіндік дәрежесі бірге тең.
Системаның
кеңістіктегі алатын орнын бірден-бір
анықтайтын өзара тәуелді болмаған
параметрлер жалпыланған координаталар
делінеді және оларды 
деп
белгілейді. Жалпыланған
координаталардың өлшем бірлігі әртүрлі
болуы мүмкін ( мәселен, метр,
радиан, м2 , м3 ).
19.1-суретте көрсетілген кривошип-шатунды
механизмнің кез-келген уақытта алатын
орнын бір ғана координата 
арқылы
анықтауға болады.
Демек, голономды байланыстағы системаның еркіндік дәрежесі оның жалпыланған координаталар санына тең. Біз бұл бөлімде тек голономды байланыстағы системаны қарастырамыз.
Егер
системаға 
голономды
болмаған байланыс қойылған болса, оның
жалпыланған координаталар арасында
белгілі бір қатынас болады. Мұндай
системаның еркіндік дәрежесі 
ге
тең.
Голономды
стационар байланыста болған механикалық
система n нүктеден
тұрады деп есептейік және оның еркіндік
дәрежесі k ға
тең болсын. Бұл голономды жүйенің
жалпыланған координаталарын 
десек,
онда қарастырылып жатқан система
нүктелерінің радиус-векторларын немесе
Декарт өстеріндегі координаталарын
жалпыланған координаталар арқылы
төмендегідей өрнектермен өрнектеуге
болады, яғни:
(19.7)
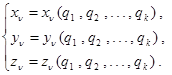(19.8)
Олай болса, голономды байланыста тұрған механикалық
системаның қозғалыс теңдеулерін жалпыланған координаталар арқылы төмендегідей түрде жазуға болады:
(19.9)
Жалпыланған координаталардан уақыт бойынша алынған бірінші туынды жалпыланған жылдамдық, екінші туынды жалпыланған үдеу
деп
аталады және
олар былай жазылады: 
(19.10)
Жалпыланған жылдамдықтың өлшем бірлігі жалпыланған координатаның өлшем бірлігі мен уақыт бірлігінің қатынасына тең.
19.4 Жалпыланған күш
Сонымен,
системага қойылған күштердің мүмкін
болған көшу кезіндегі атқарған
жұмыстарының қосындысы (19.11) формуласымен
анықталады екен. Егер (19.11) өрнекте (19.7)
ні назарға алсақ, система
нүктесінің
мүмкін болған 
көшуі
жалпыланған координаталар арқылы
төмендегідей жазылады:
(19.14)
(19.14) ті (19.11) ге апарып қойсақ:
.
(19.15)
Төмендегідей белгілеу енгізейік:
.
(19.16)
(19.16) - белгілеуге байланысты (19.15) өрнек
(19.17)
көрініске ие болады.
(19.16)
тенгликпен анықталушы 
өрнегі 
жалпыланған
координатаға сәйкес келетін жалпыланған
күш деп аталады.
Жалпыланған күшті есептеген кезде мынандай әдісті де қолдануға болады. Жалпыланған күшті есептеу үшін мүмкін болған көшудің тек ге сәйкес келетін жалпыланған координатасы ғана өзгереді деп қабылданады, қалған жалпыланған координаталар бойынша мүмкін болған көшу нөлге тең деп қаралады және орын ауыстыру кезінде мүмкін болған жұмыс есептелінеді:
.
Ол жағдайда
.
(19.18)
Сондай-ақ жалпыланған күшті аналитикалық тәсілмен төмендегідей есептеу мүмкін:
(19.19)
(19.18) ден көретініміз, жалпыланған күштің өлшемі жұмыс өлшем бірлігінің жалпыланған координат өлшем бірлігінің бөлінгеніне тең. Егер жалпыланған координат ұзындық бірлігінде өлшенсе, жалпылаған күш Ньютонда өрнектеледі, жалпыланған координата үшін бұрыш алынса, жалпыланған күш бірлігі күш моментінің бірлігі Нм- ден тұрады.
Жүйеге әсер ететін күштер потенциалдық болғанда жалпыланған күш қалай есептелінетін көрейік.
Жүйеге әсер ететін күштер потенциалдық болса,
(19.20)
(19.8) формулаға сәйкес:
Сол үшін (19.20) ны төмендегідей түрде жазу мүмкін:
(19.21)
(19.17) мен (19.21) ді салыстырсақ :
Немесе
(19.22)
келіп шығады.
Бірақ
жүйе потенцалдық энергиясы 
болғандығы
себепті жалпыланған күш потенциалдық
энергия арқылы төмендегідей өрнектеледі:
(19.23)