• 54. Байланыстар. Байланыстардың классификациясы.

19.1 - Байланыстар классификациясы

Бірнеше денеден құрылған жүйенің тепе-теңдігін қарастырғанда Лагранждың мүмкін болған көшу принціпінен пайдалану мақсатқа сай. Мүмкін болған көшу принципін беруден алдын біз байланыс түрлерімен танысайык.

Жүйе нүктелерінің қозғалысын шектейтін (яғни жүйені еріксіз ететін) шарт байланыс деп аталады. Жүйеге қойылған байланыстардың себебінен жүйе нүктелерінің координаттары, жылдамдықтары еркін өзгере алмайды. Байланыстардың жүйеге немесе оның нүктелерінің қозғалысына тигізетін әсерін схемалық түрде геометриялық сызықтар, беттер арқылы елестете аламыз. Осыған сәйкес байланыстардың денеге көрсеткен әсерлерін математикалық теңдеулер түрінде өрнектеу мүмкін. Бұл теңдеулер байланыс теңдеулері деп аталады. Байланыс теңдеулері жүйеге қатысты нүктелердің координаталары, олардың жылдамдықтары және уақыт арқылы өрнектелуі мүмкін. Жүйе нүктелерінің тек координаталарына ғана шек қоятын байланыстар геометриялық байланыстар деп аталады және төмендегідей көріністегі теңдеулер арқылы өрнектеледі:

,  (19.1)

 (19.2)

Егер байланыс жүйе нүктелерінің тек координаталарына ғана шек қоймай олардың жылдамдықтарына да шек қоятын болса, онда мұндай байланыс кинематикалық (дифференциалды) байланыс деп аталады. Бұл байланыстың теңдеуі

 (19.3)

 (19.4)

к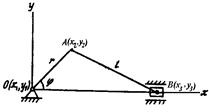

19.1 сурет

өріністерінде жазылады.

Егер (19.3) және (19.4) теңдеулер интегралланатын болса, онда ол голономды, олай болмаған жағдайда голономды емес байланыс делінеді.

Байланыс теңдеуі уақытқа тікелей тәуелді болмаса, онда мұндай байланыс стационар байланыс, ал уақытқа тікелей байланысты болса, онда мұндай байланыс стационар емес байланыс деп аталады. Демек (19.1) және (19.3) стационар, (19.2) мен (19.4) стационар емес байланыстардың теңдеулерін береді. Мәселен, 19.1-суретте көрсетілген кривошип-шатунды механизмнің кез-келген уақытта алатын орнын оның O , A және B нүктелерінің алатын орындары арқылы анықтау үшін байланыстардың төмендегідей теңдеулерін жазамыз:

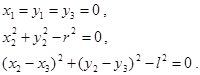
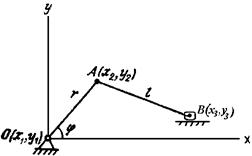
 19.2-сурет

 (19.5)

(19.5) байланыс теңдеулері О нүктенің қозғалмайтындығын , ОА және АВстержендердің ұзындықтарының өзгермейтіндігін, сонымен қатар В нүктенің  өсі бойымен жылжуын сипаттайды. (19.5) арқылы анықталатын байланыс теңдеулері уақытқа тікелей байланысты емес. Сол үшін себептен де олар стационар байланыстарды өрнектейді.

Енді кривошип-шатунды механизмнің

 19.2-сурет ползуны еденнің бетінде сырғанай отырып вертикаль бағытта   заңы бойынша гармоникалық тербелісте болсын. Онда қарастырылып жатқан жүйенің байланыс теңдеулері төмендегідей:

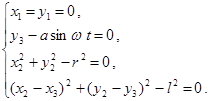 (19.6)

(19.6) теңдеудің екіншісі уақытқа байланысты. Демек , бұл байланыс стационар емес байланыс.

Жүйеге қойылған байланыстар босатылатын және босатылмайтын болып бөлінеді. Егер байланыс теңдік арқылы өрнектелсе босатылмайтын, ал байланыс теңдеуі теңсіздік түрінде өрнектелетін болса, онда ол босатылатын байланыс делінеді.

• 55. Идеал байланыстар.

Системаға қойылған байланыстардың реакция күштерінің жүйенің мүмкін болған орын ауыстыруының кезіндегі атқарған жұмыстарының қосындысы нөлге тең болса, онда мұндай байланыстар идеал байланыстар деп аталады. Система нүктелеріне қойылған байланыстардың реакция күштерін   деп белгілесек, онда идеал байланыстың шартын былай жазуға болады:

 (19.13)

56.ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ

       

(виртуальные перемещения), элементарные (бесконечно малые) перемещения, которые точки механич. системы могут совершать из занимаемого ими в данный момент времени положения, не нарушая наложенных на систему связей. В. п.— понятия чисто геометрические, не зависящие от действующих сил; они определяются только видом наложенных на систему связей и вводятся как хар-ки этих связей, показывающие, какие перемещения при наложенных связях остаются для системы возможными. Напр., если связью для точки явл. к.-н. поверхность и точка находится на ней в данный момент в положении М (рис.),

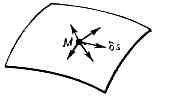
то В. п. точки в этот момент будут элем. отрезки (векторы) длиной ds, направленные по касательной к поверхности в точке М. Перемещение по любому другому направлению не будет В. п., т. к. при этом нарушится связь (точка не останется на поверхности). Понятие «В. п.» относится и к покоящейся и к движущейся точке. Если связь со временем не изменяется, то истинное элем. перемещение ds движущейся точки из положения М совпадает с одним из В. п.

Понятием «В. п.» пользуются для определения условий равновесия и ур-ний движения механич. системы, а также при нахождении числа степеней свободы системы.

57. При́нцип возмо́жных перемеще́ний — один из вариационных принципов в теоретической механике, устанавливающий общее условие равновесия механической системы. Согласно этому принципу для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма работ   всех приложенных к системе активных сил на любом возможном перемещении системы была равна нулю.

Количество линейно независимых уравнений равновесия, которые можно составить для механической системы, исходя из принципа возможных перемещений, равно количеству степеней свободы этой механической системы.

Возможными (или виртуальными) перемещениями несвободной механической системы называются воображаемые бесконечно малые перемещения, допускаемые в данный момент наложенными на систему связями (при этом время, входящее явно в уравнения нестационарных связей, считается зафиксированным). Проекции возможных перемещений на декартовы координатные оси называются вариациями декартовых координат.

Возможные перемещения, вообще говоря, не имеют отношения к процессу движения системы — они вводятся лишь для того, чтобы выявить существующие в системе соотношения сил и получить условия равновесия. Малость же перемещений нужна для того, чтобы можно было считать реакции идеальных связей неизменными.