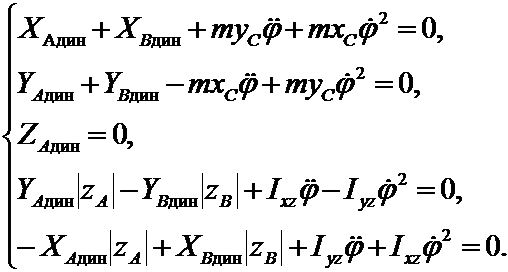• 51. Механикалық энергияның сақталу заңы.

16.29 Механикалық энергияның сақталу заңы

 

Механикалық жүйе потенциялдық күш өрісінде қозғалсын. Бұл жағдайда жүйеге қойылған сыртқы және ішкі күштер жұмыстарының қосындысы   болып, жүйе кинетикалық энергиясының өзгеруін өрнектейтін (3.128) теңдік төмендегідей жазылады:

,

немесе

 (16.134)

 

 

Мұнда   лар арқылы сәйкес жүйе нүктелеріне әсер ететің барлық күштердің бастапқы және кез келген кезге сәйкес келетін потенциалдық энергиялары белгіленген.

Жүйе потенциалдық энергиясы мен кинетикалық энергиясының қосындысы жүйеның механикалық энергиясы деп аталады.

(16.134) тен көретініміз потенциалдық күш өрісінде қозғалатын жүйенің механикалық энергиясы өзгермейды екен. Бұл механикалық эхнергияның сақталу заңы делінеді.

Материялық нүктенің механикалық энергиясының сақталу заңы төмендегідей:

 (16.135)

 Демек, потенциалдық күш өрісінде қозғалатын материялық нүктенің механикалық энергиясы өзгермейтін шама.

• 52. Даламбер принципі.

18.1 Материялық нукте үшін Даламбер принципі.  

Динамиканың мәселелерін шешкен кезде барлық әдістер Ньютон заңдарынан келіп шығатын теңдеулерге немесе динамиканың жалпы теоремаларына негізделеді.

Техникада кездесетін көптеген мәселелерді шешкен кезде механиканың жалпы принциптерінен пайдалану өте қолайлы. Бұл принциптердің бірі Даламбер принципі. Даламбер принципінде динамика теңдеулеріне статика теңдеулерінің түрі беріледі.

Еркін материялық нүкте үшін Даламбер принципін келтіріп шығару үшін

динамиканың негізгі теңдеуінен пайдаланамыз:

,

немесе

. (18.1)

Шамасы материялық нүктенің массасы мен оның үдеуінің көбейтіндісіне тең болып, бағыты үдеу векторының бағытына қарама-қарсы бағытталған вектор инерция күші деп аталады, яғни

 (18.2)

 (18.2) ні (18.1) ге қойсақ

 (18.3)келіп шығады.

( 18.3) өрнегі еркін қозғалатын материялық нүкте үшін Даламбер принципін анықтайды: Материялық нүктеге әсер ететін актив күш инерция күшімен бірге тепе-теңдікте тұрған күштер жүйесін құрайды (18.1- сурет).

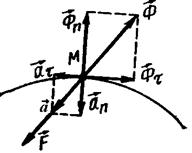
Егер материялық нүкте қисық сызық бойлап қозғалатын болса, онда инерция күші жанама және нормал құраушыларға ажратылады:

.

Мұнда немесе 18.1-сурет

 , 

Егер материялық нүкте түзу сызық бойлап қозғалатын болса, онда 

Еркін емес материялық нүкте үшін Даламбер принципі төмендегідей жазылады:  (18.4)

Бұл өрнектегі   байланыс реакция күшін білдіреді.

 

18.2 Система үшін Даламбер принципі

Механикалық жүйе бір-бірімен байланыста болған   материялық нүктелер құрамынан тұрсын. Бұл системаға әсер ететін күштерді сыртқы және ішкі күштерге ажыратсақ, онда жүйенің әр-бір нүктесі үшін Даламбер принципін төмендегідей көріністе жазамыз:

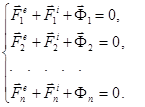 (18.5)

Демек, механикалық жүйенің әр-бір нүктесіне әсер ететін сыртқы және ішкі күштер инерция күшімен бірге алынғанда олар әр кезде тепе-теңдікті құрайды. (18.5) арқылы өрнектелген теңдеулерді бірме-бір қоссақ, онда

 (18.6)

келіп шығады. (18.6) өрнектегі  сыртқы күштердің бас векторы,  ішкі күштердің бас векторы,  инерция күштерінің бас векторы.

Ішкі күштердің қасиетіне сәйкес 

Нәтижеде (18.6) өрнегін төмендегідей көріністе жазуға болады, яғни

. (18.7)

Сонымен: Системаға әсер етуші сыртқы күштердің бас векторы мен инерция күштерінің бас векторының геометриялық қосындысы нольге тең.

Егер (18.6) - өрнекті нүктелердің   радиус-векторларына векторлік көбейтіп бұдан пайда болған натижелерді бір-біріне қоссақ, онда

 (18.8)

келіп шығады. Бұл жердегі  О нүктеге қатысты сыртқы күштердің моменті; инерция күштерінің бас моменті;  ішкі күштердің бас моменті; бірақ ішкі күштердің қасиеттерінен  . Бұл жағдайда (18.8) - өрнекті төмендегідей көріністе жазуға болады:

. (18.9)

Яғни, системага әсер етуші сыртқы күштер мен оның нүктелерінің инерция күштерінен бірер-бір орталыққа қатысты алынған моменттерінің қосындысы нөлге тең. Біргелікте алынған (18.7) және (18.9) теңдеулері механикалық жүйе үшін Даламбер принципінің векторлік көрінісін береді.

Бұл өрнектерді Декарт координата өстеріне проекцияласақ, онда механикалық жүйе үшін Даламбер принципінің аналитикалық шартын өрнектейтін теңдеулерді табамыз:

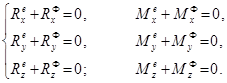 (18.10)

Егер біз системаның масса орталығының қозғалысы және кинетикалық моментінің өзгеруі жөніндегі теоремаларды

 (18.11)

 (18.12)

(18.7),(18.9) өрнектермен салыстырсақ, онда инерция күштерінің бас векторы және бірер-бір орталыққа қатысты олардың бас моментін анықтайтын формулаларды анықтаймыз, яғни

 

 (18.13)

 (18.14)

(18.13) мен (18.14) өрнектерден инерция күштерінің бас векторі дененің массасы мен инерция орталығының үдеу-векторінің көбейтіндісіне тең болып, бағыты үдеу-вектордің бағытына қарама-қарсы екені көрінеді. Инерция күштерінің бірер-бір орталыққа қатысты бас моменті системанинг осы орталыққа қатысты кинетикалық моментінен уақыт бойынша алынған бірінші туындысына тескері таңбалы өрнекке тең. (18.13) пен анықталатын векторлық шаманың жанама және нормаль құраушылары төмендегідей формулалардан табылады

 

 (18.15)

 

Енді кейбір жеке жағдайлар үшін (18.13), (18.14) формулаларынан пайдаланып инерция күштерінің бас векторі мен бас моментінің есептелетін формулаларын келтіріп шығарайық.

1.Дене ілгерілемелі қозғалыста болсын. Бұл жағдайда дене инерция орталығы төңірегінде айланбайды. Демек  болып, инерция күштері тең әсер етуші күшке келтіріледі және ол инерция күштерінің бас векторы сияқты анықталады .

2.Қозғалыстағы дене симметрия жазықтығына ие болып, ол осы жазықтыққа тік бағытталған қозғалмайтын өсь төңірегінде айналып тұрған болсын. Онда инерция күштерінің бас векторы (18.13), ал инерция күштерінің бас моменті (18.14) теңдеулерін қозғалмайтын өске проекциялаудан анықталады:

. (18.16)

 

Егер айлану өсі дене массасының орталығынан өтсе, онда   болады. 3.Дене симметрия жазықтығына ие болып, оған параллель қозғалатын болса, онда инерция күштерінің бас векторі   болады. Оның өстерге болған проекциялары , ал бас моменті    18.2- сурет

Бұл жердегі   дененің инерция орталығына қатысты инерция моменті.

Демек, жазық-параллель қозғалатын денеге қойылатын инерция күштері бір бас вектор мен бір бас моментке келтіріледі (18.2-сурет).

53

Силой инерции материальной точки (обозначается )  называется сила, равная по модулю произведению массы точки на ее ускорение и направленная в сторону противоположную ускорению. То есть

.

Принцип д’Аламбера для точки. Если в фиксированный момент движения, кроме действующих на точку сил, добавить силу инерции, то система сил будет уравновешенной.

Принцип д’Аламбера для механической системы. Если в фиксированный момент времени к каждой точке механической системы, кроме действующих сил, добавить силы инерции, то система сил будет уравновешенной.

Систему сил инерции, приложенных к точкам твердого тела, в общем случае можно заменить силой и парой сил. Сила приложена в центре приведения и равна главному вектору сил инерции, момент пары равен главному моменту сил инерции относительно центра приведения. Если центр приведения – центр масс механической системы, то

, .

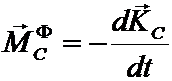При поступательном движении твердого тела система сил инерции приводится к равнодействующей, которая приложена в центре масс и определяется равенством

.

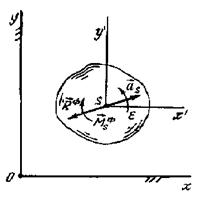
При вращении тела имеющего плоскость материальной симметрии, вокруг оси, проходящей через центр масс перпендикулярно этой плоскости, система сил приводится к паре сил, лежащей в плоскости материальной симметрии тела. Вектор момента этой пары определяется равенством

.

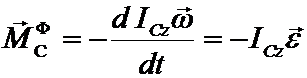Алгебраический момент пары сил инерции может быть вычислен по формулам:

.

При плоском движении твердого тела (рис. 3.8.2), имеющего плоскость материальной симметрии, система сил инерции приводится к силе и к паре сил, лежащей в плоскости материальной симметрии

, ,

где  − момент инерции относительно оси, проходящей через центр масс перпендикулярно плоскости материальной симметрии.

Аналогично рассматривается приведение системы сил инерции при вращении тела, имеющего плоскость материальной симметрии, вокруг оси, не проходящей через центр масс. При этом за центр приведения может выбираться как центр масс, так и неподвижная точка на оси вращения. Если в качестве центра приведения принимается точка , лежащая на оси вращения в плоскости симметрии, то главный момент сил инерции равен

,

где   момент инерции тела относительно оси вращения  

При движении несвободного твердого тела реакции связей, действующие на это тело, складываются из статических и добавочных динамических составляющих

,

где  − главный вектор статических реакций,  − главный вектор динамических реакций.

Статические реакции определяются из уравнений статики, а динамические  обусловлены движением тела и определяются только силами инерции.

Динамические реакции подшипников при вращении твердого тела вокруг неподвижной оси с учетом принципа д’Аламбера можно определить из следующей системы уравнений