16.28 Материялық нүкте кинетикалық энергиясының өзгеруі туралы теорема

 

М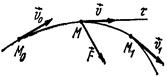 ассасы m болатын  еркін нүкте   күш әсерінде қозғалады (16.28-сурет).

Бұл жағдайда (16.129) төмендегідей жазылады:

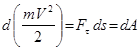 (16.131)

 

16.28-сурет

(16.123) тен көрінетіні, материялық нүкте кинетикалық энергиясының дифференциалы оған әсер ететін күштердің элементар жұмысына тең.

Материялық нүктеге әсер ететін күштің   ге көшуіндегі жұмысы мен кинетикалық энергиясы арасындағы қатынас

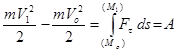 (16.132)

түрінде жазылады.

Демек, материялық нүкте кинетикалық энергиясының қандайда бір шектелген аралықтағы өзгеруі оған әсер ететін күштің осы аралықтағы жұмысына тең.

(16.130) формуланы материялық нүкте үшін төмендегідей түрде жазуға болады:

 (16.133)

• 49. Потенциалдық күш өрісі.

16.22 Потенциалдық күш өрісі. Күш функциясы. Потенциалдық күш

Материалдық нүктеге әсер ететін күштің нүкте өзінің орнын ауыстырған кездегі атқарған жұмысы нүктенің қозғалыс заңына байланысты. Дегенменде табиғатта сондай бір күштер бар (мысалы: ауырлық күші, серпімділік күші) олардың атқарған жұмыстары нүктенің қозғалыс заңына байланысты болмайды. Мұндай күштер потенциалдық күштер деп аталады.

Кеңістіктің бір бөлігіне енгізілген материялық нүктеге нүкте координаталары мен уақыттың функциясына байланысты күш әсер етсе, онда мұндай бөлік күш өрісі деп аталады. Егер уақыт өткен сайын нүктеге әсер ететін күштер өзгермесе, онда күш өрісі стационар делінеді. Сонымен қатар уақыт өткен сайын нүктеге әсер ететін күштер өзгеріп отыратын болса, яғни уақытқа тәуелді болса, онда мұндай күш өрісі стационар емес өріс деп аталады. Күш өрісіне мысал ретінде, планеталар немесе Күннің тарту күштерінің өрісі, электр немесе электромагнит өрістерін алуға болады. Бізге белгілі, нүктеге әсер ететін   күшінің элементар жұмысы төмендегі формуладан анықталады:

.

Бұл өрнектің оң жағы жалпы алғанда нүкте координаталарына байланысты бірер-бір функцияның толық дифференциалы болмайды. Егер де бұл бірер-бір   функцияның толық дифференциалы болатын күш өрісі болса, онда ол потенциалдық күш өрісі деп аталады. Бұл жағдайда

dA = dU,

немесе

 

болады.

Бұдан:

 (16.112)

табамыз.

(16.112) шартты қанағаттандырушы күш потенциалдық немесе консервативтік күш, U = U ( x , y , z ) күштік функция делінеді.

тердің көріністеріне қарап, бұл күштің потенциалдық екенін анықтау үшін (3.112) өрнектен дербес туындылар аламыз:

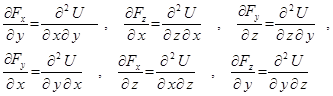
Бұдан   (16.113)

келіп шығады.

Күш проекциялары арасындағы байланыстарды анықтаушы (16.113) тың орындалуы күш өрісінің потенциалдық болуының кажетті және жеткілікті шарты.

• 50. Материялық нүкте мен механикалық жүйенің потенциалдық энергиясы.

16.23 Потенциалдық күш өрісіндегі жұмыс. Потенциалдық энергия

 

Потенциалдық күштің жұмысы туралы теореманы қарастырайық.

Күш өрісінде қозғалып бара жатқан материялық нүктеге әсер ететін потенциалдық күш жұмысы нүктенің жүрген жолына байланысты болмастан, оның тек бастапқы және соңғы орнына байланысты.

Теореманы дәлелдеу үшін   күштің элементар жұмыс өрнегін төмендегідей жазамыз:

Материялық нүкте бастапқы кезде M₀ де болып, оған қойылған күштік функция U₀ болсын. Шамалы уақыттан соң, нүкте М-ге келсін, оған тиісті күштік функция U болсын. Бұл жағдайда   күштің жұмысы

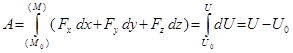 (16.114)

 

яғни, бұл күштің атқарған жұмысы функциясының тек соңғы және бастапқы орнына байланысты болады.

Күш потенциалдық болған жағдайда күш функциясы U мен бір қатарда потенциалдық энергия ұғымы да енгізіледі.

Нүктенің соңғы орны М нен бастапқы орны M₀ ге көшкен кездегі потенциалдық күштің атқарған жұмысы материялық нүктенің М жағдайдағы потенциалдық энергиясы деп аталады және төмендегідей жазылады: (16.96) формулаға сәйкес p

.

Координаттар басы нүктенің бастапқы орнына сәйкес келгенде  .

Демек, потенциалдық энергия потенциалдық функцияның теріс таңбамен алынған мәніне тең.