• 43. Қозғалыс мөлшері моментінің сақталу заңы.

16.18 Жүйе және материялық нукте кинетикалық моментінің сақталу заңы

 

Жүйе кинетикалық моментінің өзгеруі туралы теоремадан томендегі дербес жағдайлар келіп шығады.

1. Жүйеге әсер ететін сыртқы күштердің кез келген О нүктеге қатысты моменті   болса, онда жүйенің осы центрге қатысты кинетикалық моменті  дің мөлшері және бағыты өзгермейді:

 (16.82)

2. Жүйеге әсер ететін сыртқы куштердін кез келген өске қатысты моментерінің қосындысы нөлге тең болса жүйенің осы өске қатысты кинетикалық моменті өзгермейтін болады.

Мысалы. 

 (16.83)

 

Осыған ұқсас материялық нүкте кинетикалық моментінің сақталу заның баяндау мүмкін.

3. Материялық нүктеге әсер ететің күштің кез келген центрге қатысты моменті нөлге тең болса, онда нүкте қозғалыс мөлшерінің осы центрге қатысты моменті өзгермейтін болады яғни:

 

 (16.84)

4. Материялық нүктеге әсер ететің күштің кез келген өске қатысты моменті нөлге тең болса, нүктенің осы өске қатысты кинетикалық моменті озгермейтін болады.

Мысалы  .

5.Қозғалмайтын өсь төңірегінде айналып қозғалатын дененің кинетикалық моментінің сақталу заңы төмендегідей баяндалады:

Қозғалмайтын өсь төңірегінде айналатын денеге әсер ететін сыртқы күштердың айналу өсіне қарасты моменттерінің қосындысы нөлге тең болса, онда дененің осы өске қатысты кинетикалық моменті өзгермейтын болады:

немесе

. (16.85)

(16.85)-тегі   және  сәйкесінше дененің бастапқы кездегі инерция моменті және бұрыштық жылдамдығы ал  және кез келген t уақыттағы инерция моменті және бұрыштық жылдамдығы.

Қозғалмайтын өсъ төңірегін айланып қозғалатын дененің кинетикалық моментінің сақталу заңына Жуковский орындығы мысал бола алады. Жуковский орындығының горизонтал платформасына қолында тас ұстаған адам тұрғанан кейін оған бастапқы  бұрыштық жылдамдық берілсе (16.85) орынды болады. Себебі адамның тастары мен платформаның ауырлық күштері айналу өсіне параллелъ бағытталған немесе тіректі подшипникте пайда болатын реакция күші айналу өсін қиып өтеді. Сондықтан олардың айналу өсіне қатысты моменті нөлге тең.

• 44. Механикалық жүйенің қозғалмайтын өске қатысты айналмалы қозғалысының дифференциалдық теңдееуі.

16.17 Қатты дененің қозғалмайтын өсь төңірегін айнала қозғалысының дифференциялдық теңдеуі

 

Қатты дененің қозғалмайтын өсь төңірегін айнала қозғалысы техникада көп кездесетін қозғалыстардың бірі. Сол үшін дененің айналу өсіне қатысты кинетикалық моментін анықтау және дифференциялдық тендеуін келтіріп шығару аса манызға ие.

Дене қозғалмайтын Oz өсь төңірегінде   бұрыштық жылдамдықпен айналып жатқан болсын (16.16-сурет). Дененің  нуктесінен айналу өсіне дейін болған қашықтықты   десек (16.66) формулаға сәйкес:

 (16.78)

Бірақ  , соңдықтан (16.78) төмендегідей жазылады:

 (16.79)

.

 

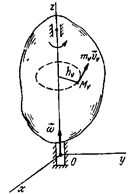
16.16-сурет

 

Демек, (16.79)-дан

 (16.80)

келіп шығады. (16.80) нен көретініміз, дененің айналу өсіне қатысты кинетикалық моменті оның осы өске қатысты инерция моментімен

бұрыштық жылдамдығының көбейтіндісіне тең болған шаманы айтады.

(16.80)-ді (16.70)-тің үшіншісіне қойсақ қатты дененің қозғалмайтын өсь төңірегін айнала қозғалысының дифференциалдық теңдеуі келіп шығады:

 

немесе:

. (16.81)

(16.81) дифференциал теңдеуді материялық нүкте қозғалысының дифференциалдық теңдеуімен (14.8) салыстырып инерция моменті айналу қозғалысындағы дененің инерттік өлшемін өрнектейтінін көреміз.