• 39. Механикалық жүйе массалары центрінің қозғалысы туралы теорема.

16.2 Механикалық жүйе массасы және масса центрі

 

Механикалық жүйенің қозғалысы тек жер күштеріне ғана байланысты болмастан, массаның үлестірілуіне де б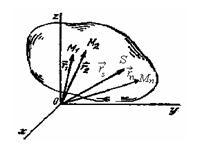 айланысты. Бұндай шамалар туралы білімдер массалар геометриясы деп аталады.

Механикалық жүйе  ,  ,...,  материялық ңүктелерден қүралған болып, олардың массалары сәйкесінше  , ,...,  болсын.

Жүйе нүктелері массаларының арифметикалық қосындысына жүйенің массасы делінеді және ол төмендегідей жазылады:

 

16.2 сурет 

Радиус векторы

 (16.4)

формула көмегінде анықталатын геометриялық нүкте-S жүйенің инерция (масса) центрі аталады. (16.4)-ті Декарт координат өстеріне проекцияласақ,

 (16.5)

келіп шығады.

Ауырлық центрінің радиус-векторы төмендегідей анықталатыны белгілі:

 

 (16.6)

 

(16.4) формуланың сыртқы көрінісі (16.6)-ке ұқсаса да мазмұны тұрғысынан бөлек. Ауырлық центрі денеге әсер ететін ауырлық күштерінің тең әсерлісінің қойылу нүктесі. Ауырлық центрі түсінігі тек қатты денелерге ғана тиісті. Инерция центрі түсінігі кез келген материялық нүктелер жүйесіне тиісті болып, ол жүйедегі масса үлестірілуінің сипаттамасынан тұрады. Және де, бұл түсінік жүйеге қандай күштер әсер ететініне байланысты емес.

(16.4), (16.5)-тен сәйкесінше

 (16.7)

және

 (16.8)

 

келіп шығады.

(16.7) жүйенің полярға қатысты статикалық моменті, ал (16.8) жүйенің OYZ, OXZ, OXY жазықтықтарға қатысты статикалық моменті деп аталады.

Жүйенің инерция орталығы оның ауырлық орталығы болса, онда осы орталыққа қатысты алынған системаның статикалық моменті нөлге тең болады:

Мұнда   мен   арқалы нүктенің инерция центрінің радиус-векторы белгіленген.

Жүйенің инерция центрінен өтетін кезкелген жазықтыққа қатысты статикалық момент те нөлге тең болады

• 40. Материялық нүкте мен материялық жүйенің қозғалысы мөлшерінің моменті.

16.14 Материялық нүкте және механикалық жүйенің қөзғалыс мөлшерінің моменті

Механика есептерін шешуде қөзғалыс мөлшері ұғымымен бір қатарда қөзғалыс мөлшері моменті немесе кинетикалық момент ұғымынан да пайданылады.   күш әсеріндегі   материялық нүкте   жылдамдықпен қозғалыста болсын (16.13-сурет).

М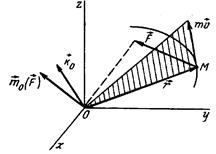 нүктенің кезкелген   центрге қатысты кинетикалық моменты деп осы нүкте радиусы - векторы мен қозғалыс мөлшері векторының векторлық көбейтіндісіне айтады және төмендегідей жазылады:

 

16.13 сурет

 (16.63)

Материялық нүкте кинетикалық моменті векторының бағыты   және   жатқан жазықтыққа перпендикуляр болады. (16.63) ті Декарт координат өстеріне проекцияласақ материялық нүкте қозғалыс мөлшерінің өске қатысты м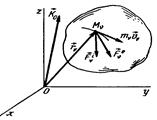 оменті келіп шығады;

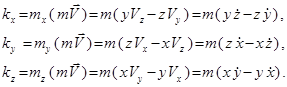 (16.64)

 

 

16.14 сурет

Кинетикалық моменттің СИ ге сәйкес өлшем бірлігі кгм/с немесе Нмс-ке тең.

Механикалық жүйенің кезкелген центрге қатысты кинетикалық моменті жүйені құрайтын барлық материялық нүктелердің осы центрге қатысты кинетикалық моменттерінің геометриялық қосындысына тең (16.14-сурет).

 (16.65)

 

(16.65) ті Декарт координата өстеріне проекциялаймыз:

 

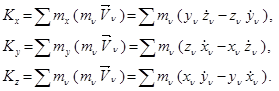 (16.66)

• 42. Материялық нүкте мен материялық жүйенің қозғалыс мөлшер моментінің өзгеруі туралы теорема.

16.15 Механикалық жүйе және материялық нүкте кинетикалық моменттерінің өзгеруі турасындағы теорема

 

Жүйе кинетикалық моментінің өзгеруі туралы теореманы келтіріп шығару үшін (16.65) тен уақыт бойынша туынды аламыз:

 (16.67)

Мұндағы

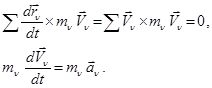
Жүйенің   нүктесіне қойылған сыртқы және ішкі күштердің тең әсерлі күштерін сәйкесінше  ,   (16.14-сурет) десек, (16.18)-ге сәйкес:

.

Нәтижеде (16.67) төмндегідей жазылады:

.

Ішкі күштердің қасиеттерін еске алсақ, яғни

,

онда

 

 , (16.68)

немесе

 (16.69)

 

(16.69) өрнек жүйе кинетикалық моментінің өзгеруі туралы теореманы береді: механикалық жүйенің центрге қатысты кинетикалық моментінен уақыт бойынша алынған бірінші ретті туынды оған әсер ететін сыртқы күштердің осы центрге қатысты бас моментіне тең.

(16.69) ді Декарт координат өстеріне проекциялаймыз:

 (16.70)

Мұндағы

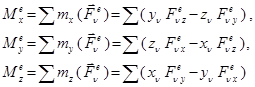 (16.71)

 

(16.70) ті төмендегідей баяндау мүмкін: механикалық жүйенің қозғалмайтын өске қатысты кинетикалық моментінен уақыт бойынша алынған бірінші ретті туынды оған әсер ететін сыртқы күштердің осы өске қатысты моменттерінің қосындысына тең.

(16.69) дан дербес жағдай ретінде материялық нүкте қозғалыс мөлшерінің центрге қатысты моментінің өзгеруі туралы теореманы алуға болады: материялдық нүкте қозғалыс мөлшерінің кез-келген центрге қатысты моментінен уакыт бойынша алынган бірінші туынды нүктеге әсер ететін күштің осы центрге қатысты моментіне тең:

 (16.72)

немесе

. (16.73)

Егер материялық нүкте бірнеше күштер әсерінде болса (16.72) немесе (16.73) тегі   - ті ос ы күштердің тең әсерлісі деп қарастыру керек.

(16.73)-ті Декарт координат өстеріне проекцияласақ, материялық нүкте қозғалыс мөлшерінің өске қатысты моментінің өзгеруі туралы теорема келіп шығады.

, (16.74)

немесе

 

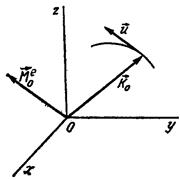
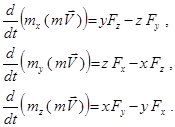 (16.75)

Демек, материялық нүкте қозғалыс мөлшерінің кез-келген өске қатысты моментінен уақыт бойынша алынған бірінші туынды оған әсер ететін күштің осы өске қатысты моментіне тең.