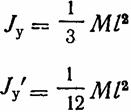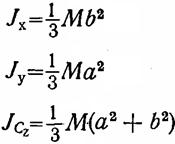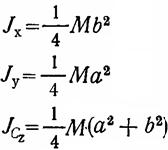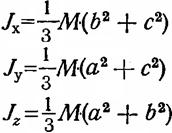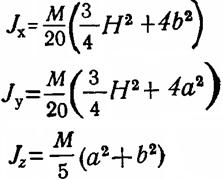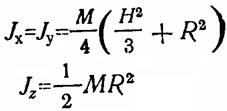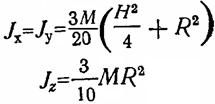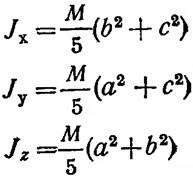- •4*Қос күштер. Қос күштер жүйесінің тепе-теңдік шарттары. Қос күш қос күш моменті.
- •1 Салдар.
- •Жылтыр бет.
- •Жылжымалы топса.
- •Жылжымайтын топса.
- •Жіп, арқан, шынжыр, салмақсыз стержень.
- •Подшипник.
- •Подпятник
- •Сфералық топса.
- •*3 Бiр нүктеге жинақталған күштер жүйесiнiң тепе-теңдiк шарты
- •7* . Жазықтыққа кез келген бағыттағы күштер системасының аналитикалық тепе теңдік шарттары
- •8* Айналу үйкелісі және домалау үйкелісі. Домалау үйкелісі. Айналу үйкелісі.
- •10* Ауырлық центрі. Қарапайым біртекті денелердің ауырлық центрлері
- •11* Нүкте қозғалысының берілу әдістері
- •12* Нүктенің әр түрлі берілу әдістегі жылдамдығы Нүктенің жылдамдығы
- •13* Нүктенің векторлық және координаталық берілу әдістегі үдеуілері- Нүктенің үдеуі
- •14* Нүктенің табиғи берілу әдістегі үдеуі.
- •15* Қатты дененің ілгермелі қозғалысы
- •17* Қатты дененің жазық-параллель қозғалысы.
- •18* Қатты дененің жазық-параллель қозғалысытағы нүктелеріның жылдамдығы
- •19* Жылдамдықтардың лездік центрі.
- •21* Нүктенің күрделі қозғалысы - Нүктенің күрделі қозғалысы. Қатты дененің күрделі қозғалысы
- •22* Жылдамдықтарды қосу туралы теорема - Жылдамдықтарды қосу туралы теорема
- •24* Қатты дененің күрделі қозғалысы. - Нүкте немесе қатты дене бірнеше қозғалысқа қатысса, онда бұл нүктенің немесе қатты дененің қозғалысын күрделі қозғалыс деп атайды.
- •25* Динамиканың негігі зандары
- •27* Нүкте динамикасының екі мәселесі. -
- •28. Дифференциальные уравнения относительного движения материальной точки
- •29. Условия относительного покоя
- •33. Теорема Гюйгенса-Штейнера
- •41. Момент количества движения твердого тела, вращающегося вокруг неподвижной оси
- •31. Механикалық жүйенің және қатты дененің өске және центрге қатысты инерция моменттері.
- •32. Қарапайым біртекті қатты денелердің инерция моменттері.
- •16.4 Кейбір бір текті денелердің инерция моменттері
- •34. Сыртқы және ішкі күштер, ішкі күштердің қасиеттері.
- •16.1 Механикалык жүйе. Ішкі және сыртқы күштер.
- •35. Материялық жүйенің дифференциалдық теңдеулері.
- •16.5 Механикалық жүйе қозғалысының дифференциал теңдеулері
- •36. Материялық нүкте мен материялық жүйенің қозғалыс мөлшерінің. Күштің импульсы.
- •16.10 Материялық нүкте және механикалық жүйенің қозғалыс мөлшері
- •16.9 Күш импульсі
- •39. Механикалық жүйе массалары центрінің қозғалысы туралы теорема.
- •16.2 Механикалық жүйе массасы және масса центрі
- •40. Материялық нүкте мен материялық жүйенің қозғалысы мөлшерінің моменті.
- •16.14 Материялық нүкте және механикалық жүйенің қөзғалыс мөлшерінің моменті
- •42. Материялық нүкте мен материялық жүйенің қозғалыс мөлшер моментінің өзгеруі туралы теорема.
- •16.15 Механикалық жүйе және материялық нүкте кинетикалық моменттерінің өзгеруі турасындағы теорема
- •43. Қозғалыс мөлшері моментінің сақталу заңы.
- •16.18 Жүйе және материялық нукте кинетикалық моментінің сақталу заңы
- •44. Механикалық жүйенің қозғалмайтын өске қатысты айналмалы қозғалысының дифференциалдық теңдееуі.
- •16.17 Қатты дененің қозғалмайтын өсь төңірегін айнала қозғалысының дифференциялдық теңдеуі
- •45. Материялық нүкте мен механикалық жүйенің кинетикалық энергиясы.
- •16.24 Материялық нүкте және механикалық жүйенің кинетикалық энергиясы
- •16.25 Кёниг теоремасы
- •48. Материялық нүкте мен механикалық жүйенің кинетикалық энергияның өзгеруі туралы теоремалар.
- •16.27 Жүйе кинетикалық энергиясының өзгеруі туралы теорема
- •16.28 Материялық нүкте кинетикалық энергиясының өзгеруі туралы теорема
- •49. Потенциалдық күш өрісі.
- •16.22 Потенциалдық күш өрісі. Күш функциясы. Потенциалдық күш
- •50. Материялық нүкте мен механикалық жүйенің потенциалдық энергиясы.
- •16.23 Потенциалдық күш өрісіндегі жұмыс. Потенциалдық энергия
- •51. Механикалық энергияның сақталу заңы.
- •16.29 Механикалық энергияның сақталу заңы
- •52. Даламбер принципі.
- •54. Байланыстар. Байланыстардың классификациясы.
- •55. Идеал байланыстар.
- •58. Жалпыланған координаттар және жалпыланған күштер.
- •19.2. Жалпыланған координаттар. Жүйенің еркіндік дәрежесі.
- •19.4 Жалпыланған күш
- •60. Динамиканың жалпы теңдеуі.
- •20.1 Динамиканың жалпы теңдеуі
- •59. Условие равновесия в обобщенных координатах
32. Қарапайым біртекті қатты денелердің инерция моменттері.
16.4 Кейбір бір текті денелердің инерция моменттері
Дене түрі |
Дене формасы |
Инерция моменті |
1 |
2 |
3 |
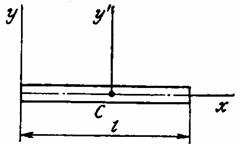
Жіңішке стержень |
|
|
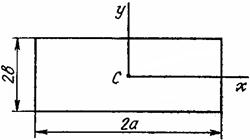
Тік төртбұрыш |
|
|
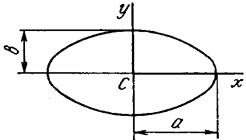
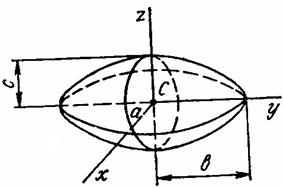
эллипс |
|
|
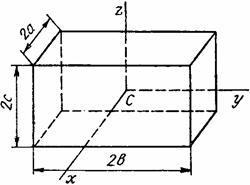
Тік бұрышты параллелепипед |
|
|
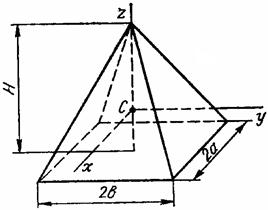
Тік бұрышты пирамида |
|
|
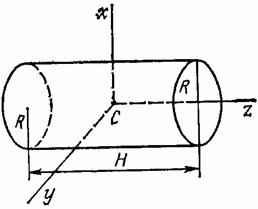
Дөнгелек цилиндр |
|
|
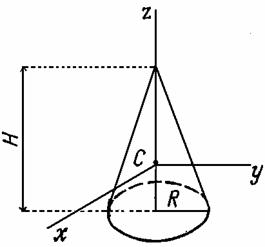
Дөңгелек конус |
|
|
эллипсоид |
|
|
34. Сыртқы және ішкі күштер, ішкі күштердің қасиеттері.
16.1 Механикалык жүйе. Ішкі және сыртқы күштер.
Қозғалыстары өзара бір-бірімен байланыста болған материялық нүктелер жүйесі механикалық жүйе делінеді. Механикалық жүйе еркін және байланыста болуы мүмкін.
Механикалық жүйе нүктелерінің қозғалысы ешқандай себеппен шектелмеген, яғни нүктелер арасындағы байланыстар өзара жердің тартылу күшінен ғана тұратын болса, осы жүйе еркін болады.
Механикалық жүйе нүктелерінің қозғалысы бір себеппен шектелген, яғни осы жүйе нүктелеріне байланыстар қойылған болса, ол байланыстағы жүйе деп атлады.
Еркін механикалық жүйеге мысал ретінде Күн жүйесін алу мүмкін, себебі Күн және планеталар өзара бүкіл әлемдік тартылыс күші әсерінде болады.
Байлныстағы механикалық жүйеге әр қандай машина механизмдерін мысал етуге болады. Себебі машина механизмдерінің бөліктері бір-бірімен топсалар, стержендер, қайыстар немесе тісті дөңгелектер арқылы байланысқан болады.
Жүйенің кезкелген екі нүктесі арасындағы қашықтық өзгермейтін болса, ол өзгермейтін жүйе деп аталады. Бұндай жүйеге қатты дене мысал болады.
М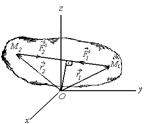 еханикалык
жүйеге әсер ететін күштер шартты түрде
ішкі және сыртқы күштерге бөлінеді.
Механикалық жүйені құрайтын нүктелердің
өзара бір-біріне болған әсері ішкі
күштер делінеді.
еханикалык
жүйеге әсер ететін күштер шартты түрде
ішкі және сыртқы күштерге бөлінеді.
Механикалық жүйені құрайтын нүктелердің
өзара бір-біріне болған әсері ішкі
күштер делінеді.
Механикалық
жүйе құрамына енбейтін денелер (нүктелер)
тарапынан (16.1-сурет) қойылған күштер
сыртқы күштер деп аталады. Ішкі күштер ![]() ,
сыртқы
,
сыртқы
16.1
сурет күштер ![]() сондай-ақ
ішкі күштер бас векторы
сондай-ақ
ішкі күштер бас векторы ![]() ,
,
сыртқы
күштер бас векторы ![]() мен
белгіленеді.
мен
белгіленеді.
Бір жүйе үшін сыртқы деп есептелетін күш екінші жүйеге қатысты ішкі күш болуы да мүмкін. Мысалы бүкіл Күн жүйесінің қозғалысы зерттелгенде планеталардың өзара тартылыс күші ішкі күш есептелінеді. Жердің өзінің орбитасы бойымен күн төңірегіндегі қозғалысы зерттелгенде тартылыс күші сыртқы күш болады.
Ішкі күштер қасиеттерін қарастырамыз.
1.Жүйе ішкі күштерінің бас векторы нөлге тең. Шынында да Ньютонның 3-заңына сәйкес жүйенің кезкелген екі және нүктелерінің өзара әсерлесу күштері мөлшер жағынан тең және бір түзу сызық бойымен қарама-қарсы жаққа бағытталған (16.1-сурет)
![]()
бұдан ![]() .
Бұл қорытындыны жүйенің барлық нүктелері
үшін қолдану мүмкін. Сонымен,
.
Бұл қорытындыны жүйенің барлық нүктелері
үшін қолдану мүмкін. Сонымен,
![]() .
(16.1)
.
(16.1)
(16.1)-ді Декарт координата өстеріне проекцияласақ,
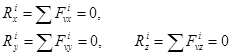 (16.2)
(16.2)
алынады.
2. Ішкі күштердің бір нүктеге қатысты бас моменті нөлге тең.
![]() (16.3)
(16.3)
Бұл қасиеттің орынды екендігі Ньютонның үшінші заңын пайдаланып көрсетіледі.
(16.3)-ті Декарт координата өстеріне проекцияласақ,
![]()
келіп шығады.
Ішкі күштердің бұл қасиеттерінен ішкі кұштер өзара тепе-теңдікте болады деген нәтиже келіп шықпайды, себебі бұл күштер жүйенің әртүрлі нүктелеріне қойылған. Сол үшін ішкі күштер жүйе нүктелерінің озара көшуіне әсер етеді. Абсолют қатты дене қарастырылғанда ішкі күштер тепе-теңдікте болатын күштер жүйесін құрайды.