29. Условия относительного покоя

F+R+Jk=0

Найдем такие системы координат, в которых выполняется первый закон Ньютона, для этого достаточно потребовать, чтобы при отсутствии сил точка двигалась равномерно и прямолинейно

Je+Jk=0

Для того, чтобы подвижная система координат была инерциальной, достаточно, чтобы

a=0

ώ=0

ma=F+R

33. Теорема Гюйгенса-Штейнера

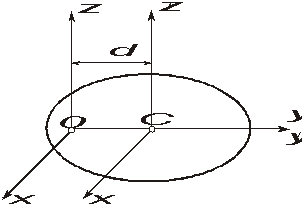
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

где — полная масса тела.

41. Момент количества движения твердого тела, вращающегося вокруг неподвижной оси

Ко=J2 m2

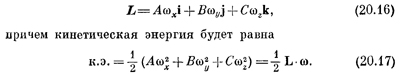
30* Механикалық жүйенің қозғалысы тек жер күштеріне ғана байланысты болмастан, массаның үлестірілуіне де байланысты. Бұндай шамалар туралы білімдер массалар геометриясы деп аталады.

Механикалық жүйе  ,  ,...,  материялық ңүктелерден қүралған болып, олардың массалары сәйкесінше  , ,...,  болсын.

Жүйе нүктелері массаларының арифметикалық қосындысына жүйенің массасы делінеді және ол төмендегідей жазылады:

 

16.2 сурет 

Радиус векторы

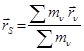 (16.4)

формула көмегінде анықталатын геометриялық нүкте-S жүйенің инерция (масса) центрі аталады. (16.4)-ті Декарт координат өстеріне проекцияласақ,

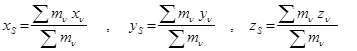 (16.5)

келіп шығады.

Ауырлық центрінің радиус-векторы төмендегідей анықталатыны белгілі:

 

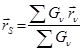 (16.6)

 

(16.4) формуланың сыртқы көрінісі (16.6)-ке ұқсаса да мазмұны тұрғысынан бөлек. Ауырлық центрі денеге әсер ететін ауырлық күштерінің тең әсерлісінің қойылу нүктесі. Ауырлық центрі түсінігі тек қатты денелерге ғана тиісті. Инерция центрі түсінігі кез келген материялық нүктелер жүйесіне тиісті болып, ол жүйедегі масса үлестірілуінің сипаттамасынан тұрады. Және де, бұл түсінік жүйеге қандай күштер әсер ететініне байланысты емес.

(16.4), (16.5)-тен сәйкесінше

 (16.7)

және

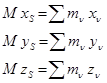 (16.8)

 

келіп шығады.

(16.7) жүйенің полярға қатысты статикалық моменті, ал (16.8) жүйенің OYZ, OXZ, OXY жазықтықтарға қатысты статикалық моменті деп аталады.

Жүйенің инерция орталығы оның ауырлық орталығы болса, онда осы орталыққа қатысты алынған системаның статикалық моменті нөлге тең болады:

Мұнда   мен   арқалы нүктенің инерция центрінің радиус-векторы белгіленген.

Жүйенің инерция центрінен өтетін кезкелген жазықтыққа қатысты статикалық момент те нөлге тең болады.

• 31. Механикалық жүйенің және қатты дененің өске және центрге қатысты инерция моменттері.

Жүйенің инерция моменті. Инерция радиусы

 

Масса центрінің орны жүйеде масса үлестірімін толық сипаттамайды. Мысалы: Oz өстен h қашықтықта тұратын екі бірдей Ажәне В шарлардың орнын бірдей қашықтыққа өзгертсек (16.3-сурет), жүйе масса центрінің орны өзгермейді. Бірақ жүйеде масса үлестірімі өзгереді, яғни А және В шарлардың Oz өсь төңірегінде айналуы жылдамдайды не баяулайды.

 

 

 

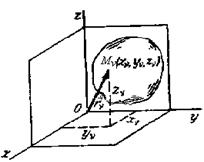
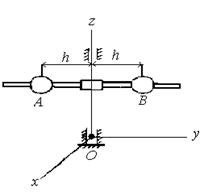
 16.3 сурет 16.4 сурет

Механикалық жүйенің (системаның) айланған кездегі оның массасының үлестірілуін анықтайтын шама инерция моменті деп аталады. Системаның

өске, нүктеге және жазықтыққа қатысты инерция моменттері ұғымдарымен танысып шығайық. Бұл үшін кез келген О нүктеден өтетін бір-біріне перпендикуляр үш өсті және үш жазықтықты алайық (16.4-сурет). Системаның өске қатысты инерция моменті деп сол жүйенің әрбір бөлшегінің массасын осы бөлшектен өске дейінгі болған жақын арақашықтықтың квадратына көбейткендегі пайда болған шаманы бүтін система бөлшектері бойынша алып қосқанға айтады.

Механикалық жүйенің Oz өсіне қатысты инерция моментін   деп белгілесек, онда берген анықтамаға сәйкес

. (16.9)

Бұл жердегі   нүктеден өске дейінгі болған арақашықтық.

Инерция моментінің СИ системадағы өлшем бірлігі кгм²,техникалық жүйеде кгмс² болады. Өске қатысты инерция моментін есептегенде система бөлшектерінен өске дейінгі болған арақашықтықты осы бөлшектердің координаталары арқылы өрнектеуге болады. Егер   нүктенің координаталарын   деп белгілесек, онда системаның Ox , Oy , Oz өстерге қатысты инерция моменттері төмендегідей жазылады:

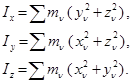 (16.10)

Системаның координаталар басына қатысты инерция моменті

 

 (16.11)

болады.

Егер (16.10) өрнектерді бір-бірімен өзара қосып, табылғанды (16.11) мен салыстырсақ төмендегідей байланыс шығады:

 (16.12)

Системаның yOz , xOz және xOy жазықтықтарға қатысты инерция моменттері

 

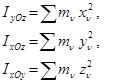 (16.13)

формулалардан табылады.

Бір текті дененің кез келген өске қатысты инерция моментін оның осы өске қатысты инерция радиусы деп аталатын сызықтық шама   ны пайдаланып та анықтауға болады, яғни

 (16.14)

Бір текті дененің өске қатысты иенрция радиусы тәжірибелер көмегінде анықталып, кестелерде берілген болады.

Егер дененің кезкелген өске қатысты инерция моменті анық болса , оның осы өске қатысты инерция радиусын (16.14)-ке сәйкес

 (16.15)

формуладан анықтау мүмкін.

Қатты дененнің центрден тепкіш инерция моменттері төмендегідей табылады:

 (16.16)