27* Нүкте динамикасының екі мәселесі. -

Материялық нүктенің қозғалыс заңы белгілі болса, динамиканың бірінші мәселесін шешу оңай. Бұл мәселе төмендегі ретпен шешіледі:

1.Егер мәселе шартында санақ жүйесі берілмеген болса, ол таңдап алынады.

2.Материялық нүктеге әсер ететін күштер суретте кескінделеді.

3.Егер нүкте байланыста болса, ол ойша байланыстан босатылады және оның реакция күштері суретте көрсетіледі

4.Таңдап алынған санақ жүйесінде материялық нүкте қозғалысының дифференциал теңдеулері құрылады.

5.Берілген қозғалыс заңынан пайдаланып, материялық нүкте үдеуінің санақ жүйесіне қатысты проекциялары анықталады.

6.Үдеудің табылған проекциялары дифференциал теңдеулерге қойылып белгісіз күш анықталады.

Техникаға қатысты көптеген мәселелерді шешу динамиканың екінші негізгі мәселесін шешуге алып келеді.

Динамиканың екінші негізгі мәселесі нүктеге қойылған күш қандай сипатта өзгеруіне қарай диффренциал теңдеулерді шешудің түрлі тәсілдерін қолданады.

Ең қарапайым жағдай күш тұрақты болғанда. Кейбір жағдайлар күш уақыттың, немесе нүкте орнының, немесе нүкте жылдамдығының функциясы болуы мүмкін. Сондай-ақ бір жола уақыт, жол, жылдамдық және кейде үдеу функциясынан тұратын жағдайлар кездеседі.

Динамиканың бұл негізгі мәселесін шешу үшін (14.8), (14.9), (14.13)-(14.16) түріндегі екінші реттік диффренциал теңдеулердің бірін құру және оны интегралдау керек. Интегралдау нәтижесінде дифференциал теңдеулердің шешіміне кез-келген тұрақтылар енеді. Әрбір нақты есепті шешкен кезде бұл тұрақтыларды анықтау керек. Тұрақтыларды анықтау үшін материялық нүктенің бастапқы уақыттағы алған орны мен жылдамдығын өрнектейтін шарттардан пайдаланылады.

Динамиканың екінші негізгі мәселесі бойынша дифференциал теңдеулер шешіліп, нүктенің қозғалыс заңы анықталады. Бұл жол динамиканың кері мәселесі деп те аталады.

Динамиканың кері мәселесі төмендегі ретпен шешіледі.

1. Егер есеп шартында санақ жүйесі берілмеген болса, онда ол таңдап алынады.

2.Суретте материялық нүктенің кез келген жағдайы белгіленіп, оған әсер ететін күштер кескінделеді.

3. Егер нүкте байланыста болса, оны байланыстан ойша босатып, байланыс реакция күштері суретте көрсетіледі.

4. Материялық нүкте қозғалысының бастапқы шарттары жазылады.

5. Материялық нүкте қозғалысының таңдап алынған санақ жүйесіндегі дифференциал теңдеулері құрылады.

7. Бастапқы шарттарды пайдаланып, интегралдау нәтижесінде алынған тұрақтылар анықталады.

8. Материялық нүктенің анықталған қозғалыс теңдеуінен керек болған белгісіздер табылады.

28. Дифференциальные уравнения относительного движения материальной точки

Уравнение второго основного закона динамики для абсолютного движения точки массой m имеет вид

Абсолютное ускорение точки в сложном движении определяется как геометрическая сумма трех ускорений: переносного aпер , относительного aотн и кориолисова aкор , т.е.

Проецируя уравнение (7.3) на оси подвижной декартовой системы координат, получим дифференциальные уравнения относительного движения точки

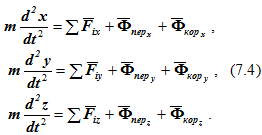
Дифференциальные уравнения относительного движения отличаются от дифференциальных уравнений абсолютного движения наличием в правой части уравнений проекций на соответствующие оси переносной и кориолисовой сил инерции.