Теория квазиоптимума

Возникновение монополии даже на одном рынке нарушает Парето-эффективное распределение ресурсов во всей экономике:

; P_X^M>P_X^C.

В результате искажаются:

• цены на всех рынках, а не только на монополизированном;

• объемы производства, по сравнению с эффективными объемами производства на конкурентных рынках;

• распределение ресурсов на всех рынках, поскольку неиспользуемые монополией ресурсы поглощаются другими отраслями.

Следствие. В случае, когда в одной отрасли или группе отраслей искажения не могут быть устранены, лучше отказаться от эффективности в другой отрасли (отраслях) с тем, чтобы сбалансировать экономику в целом.

Поскольку общее равновесие трудно достижимо, наиболее реальным является субоптимальное решение задачи оптимизации функционирования общественного производства (так называемая ситуация «second best»), достигаемое путем государственного регулирования экономики.

Пример № 1

Общее экономическое равновесие в потреблении (распределении). Кривая доступных полезностей

Пусть экономика состоит из двух групп потребителей (А и В), каждая из которых потребляет два вида продуктов (№1 и №2) и обладает соответствующей функцией полезности: , . Первоначальные запасы благ в данной экономике у этих групп составляют соответственно , , , .

Определим конечное распределение продуктов между потребителями.

Поскольку функция полезности в данном примере имеет вид зависимостей Кобба–Дугласа, функции маршалианского спроса на соответствующие товары для каждой группы потребителей задаются следующими соотношениями:

где и – доходы двух групп потребителей.

Принимаем цену второго товара равной единице. Тогда функции спроса на него принимают вид:

Доходы можно найти исходя из первоначальных запасов продуктов у потребителей, но до этого необходимо найти цену первого блага

Каждое из двух предыдущих равенств дает

Тогда

Отсюда можно получить конечное распределение продуктов между потребителями:

Выведем уравнение линии контрактов. Для этого рассчитаем предельные нормы замещения первым благом второго для каждого потребителя:

, .

Кроме того, из ресурсных ограничений для каждой из групп потребителей известно, что запасы первого продукта в данной экономике составляют 12 ед., а капитала – 6 ед. Поэтому для данной экономики справедливы следующие соотношения между потреблением продуктов этими двумя группами: =12– , =6– . Из данных условий получаем отношения между затратами факторов производства:

,

откуда следует уравнение кривой контрактов:

=0,5 .

Ее график будет диагональю в прямоугольнике Эджуорта (рис. 12).

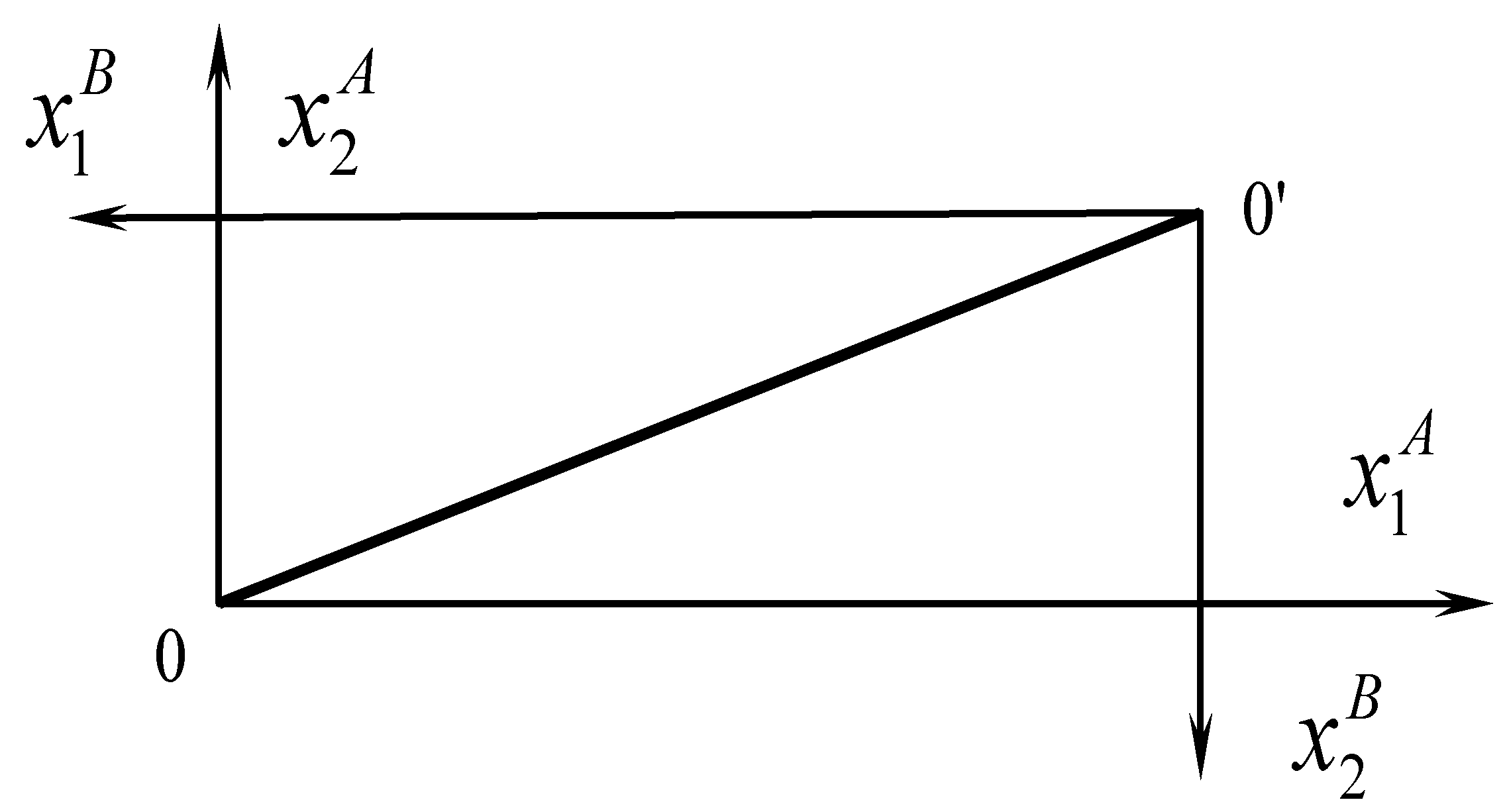
Рис. 12. Пример линии контрактов

В силу линейности линии контрактов состояние общего равновесия в потреблении имеет существенную особенность: относительная цена первого товара равна 0,5 независимо от первоначального распределения запаса товаров между потребителями

.

Выведем теперь уравнение потребительских возможностей (границу доступных полезностей) общества. Используя уравнение линии контрактов, получаем соотношение между объемом потребления второго товара индивидом А и уровнем реализуемой им полезности:

,

.

Тогда уровень полезности потребителя В может быть следующим образом выражен через уровень полезности потребителя А:

На рис. 13 построена граница доступных полезностей. Первая производная функции полезности потребителя В по полезности индивида A – отрицательна, значит, зависимость убывающая. Вторая производная при любых положительных значениях функции полезности потребителя А положительна, что свидетельствует о том, что зависимость выпукла (вниз). Точки пересечения границы возможных полезностей с осями координат показывают максимально возможные величины полезностей каждого из потребителей в том случае, если все запасы благ обоих благ будут находиться в собственности соответствующего потребителя.

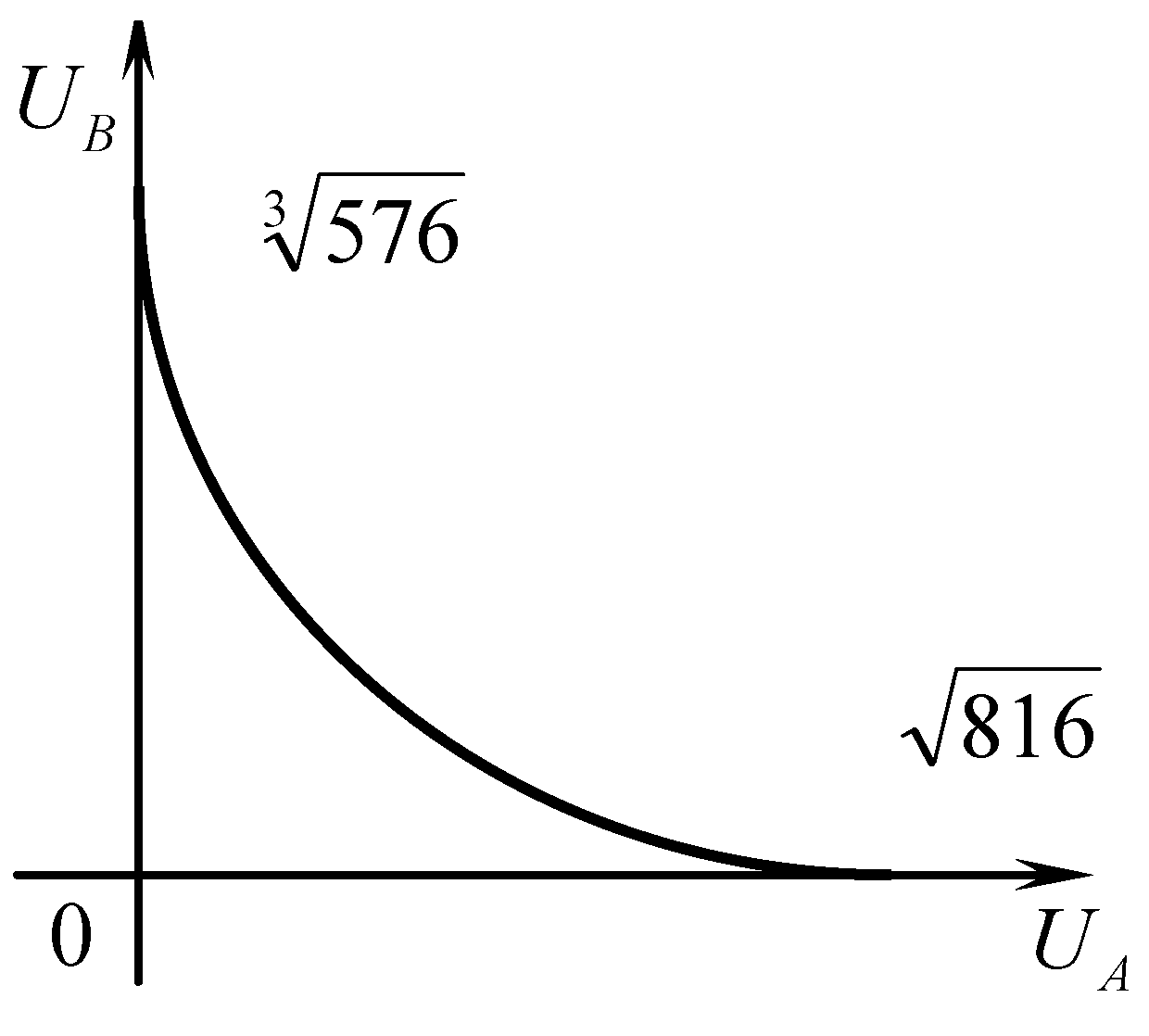
Рис. 13

Пример № 2

Общее экономическое равновесие в производстве. Кривая производственных возможностей общества

Пусть экономика состоит из двух групп производителей, каждая из которых производит продукт определенного вида – X или Y – с использованием таких факторов производства, как труд L и капитал K. Производственные функции каждой из групп производителей имеют вид: , . Первоначальные запасы труда и капитала в данной экономике у этих групп составляют соответственно K_X=2, L_X=6, K_Y=4, L_Y=6. Выведем уравнение кривой производственных возможностей. Для этого рассчитаем предельные нормы технологического замещения капитала трудом в производстве ресурсов X и Y:

, (1)

Кроме того, из ресурсных ограничений для каждой из групп производителей известно, что запасы труда в данной экономике составляют 12 ед., а капитала – 6 ед. Поэтому для данной экономики справедливы следующие соотношения между затратами капитала и труда двух групп: K_Y=6–K_X, L_Y=12–L_X. Из данных условий получаем отношения между затратами факторов производства:

, (2)

откуда следует уравнение кривой производственных контрактов:

K_X=0,5L_X. (3)

Ее график будет диагональю в прямоугольнике Эджуорта (рис. 14).

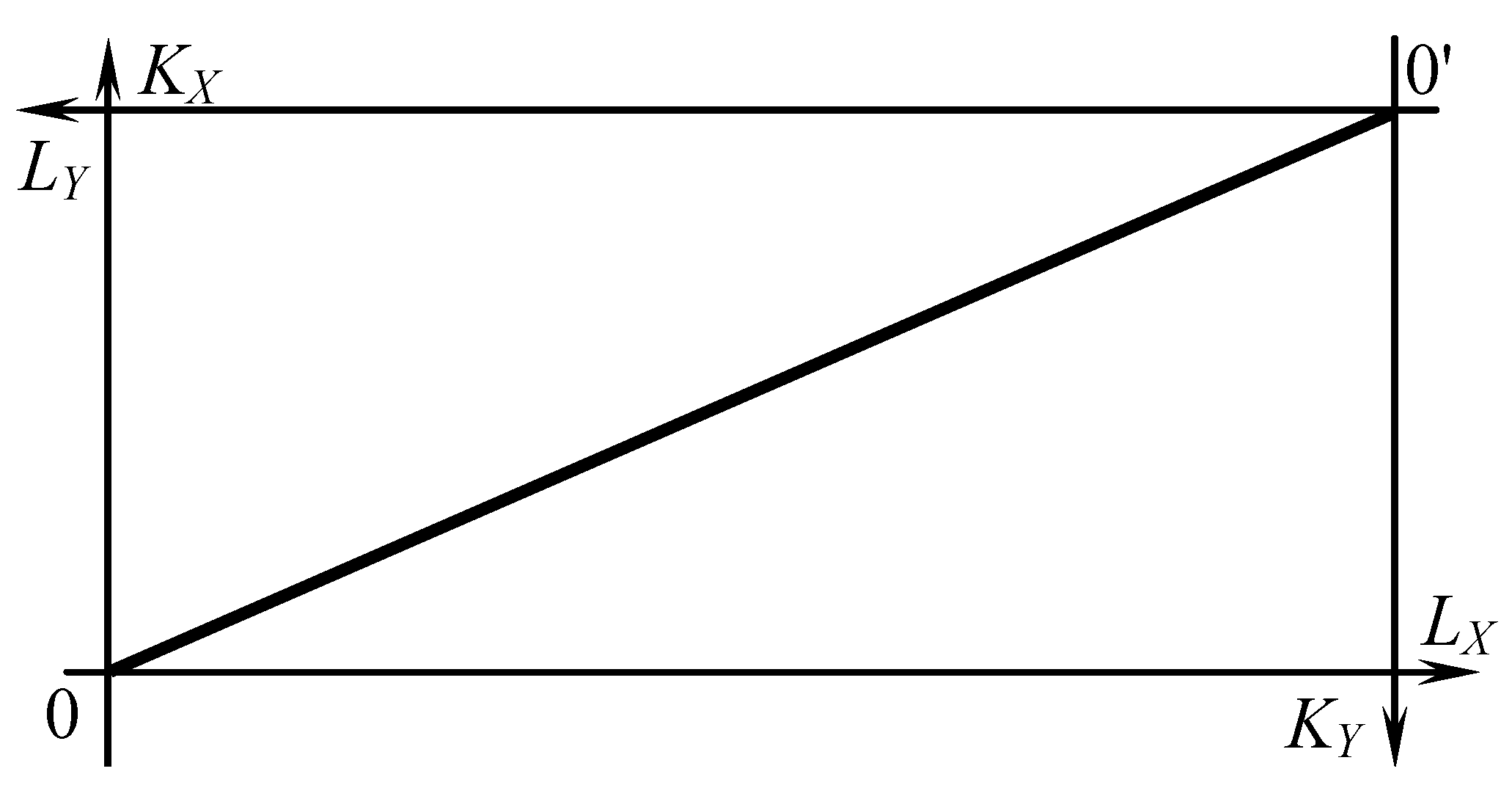
Рис. 14. Пример линии производственных контрактов

Относительная ставка заработной платы равна:

. (4)

Если арендная цена капитала равна единице, то абсолютное значение ставки заработной платы составит 0,5. Поскольку производственные функции в данной задаче имеют вид зависимостей Кобба–Дугласа, функции спроса на капитал и труд для каждой группы производителей задаются следующими соотношениями:

(5)

где M_X и M_Y – доходы двух групп производителей.

Если цена капитала равна единице, то функции спроса на этот фактор производства принимают вид:

K_X=0,5TC_X, K_Y=0,5TC_Y. (6)

Величину издержек производства можно найти исходя из первоначальных запасов факторов у производителей:

TC_X=2P_K+6P_L=2+6P_L=5, TC_Y=4P_K+6P_L=4+6P_L=7. (7)

Отсюда можно получить конечное распределение ресурсов у производителей: K_X*=2,5, L_X*=5, K_Y*=3,5, L_Y*=7.

Ставку заработной платы можно также найти исходя из закона Вальраса, в соответствии с которым

K=0,5(2P_K+6P_L)+0,5(4P_K+6P_L)=6; (8)

. (9)

Каждое из равенств (8) и (9) дает P_L=0,5, поскольку P_K, по предположению, равна 1.

Выведем теперь уравнение производственных возможностей общества. Используя уравнение линии контрактов (3), получаем соотношение для затрат капитала производителем X:

, то есть (10)

Тогда объем производства Y следующим образом выражается через объем производства X:

.(11)

На рис. 15 построена граница производственных возможностей общества. Ее первая и вторая производные отрицательны при любых возможных значениях X, что свидетельствует о необходимости отказа от выпуска некоторого количества Y при увеличении производства X и при этом о росте соответствующих альтернативных издержек. Точки пересечения границы производственных возможностей с осями координат показывают максимально возможные объемы выпуска благ в том случае, если все ресурсы будут находиться в собственности соответствующего производителя.

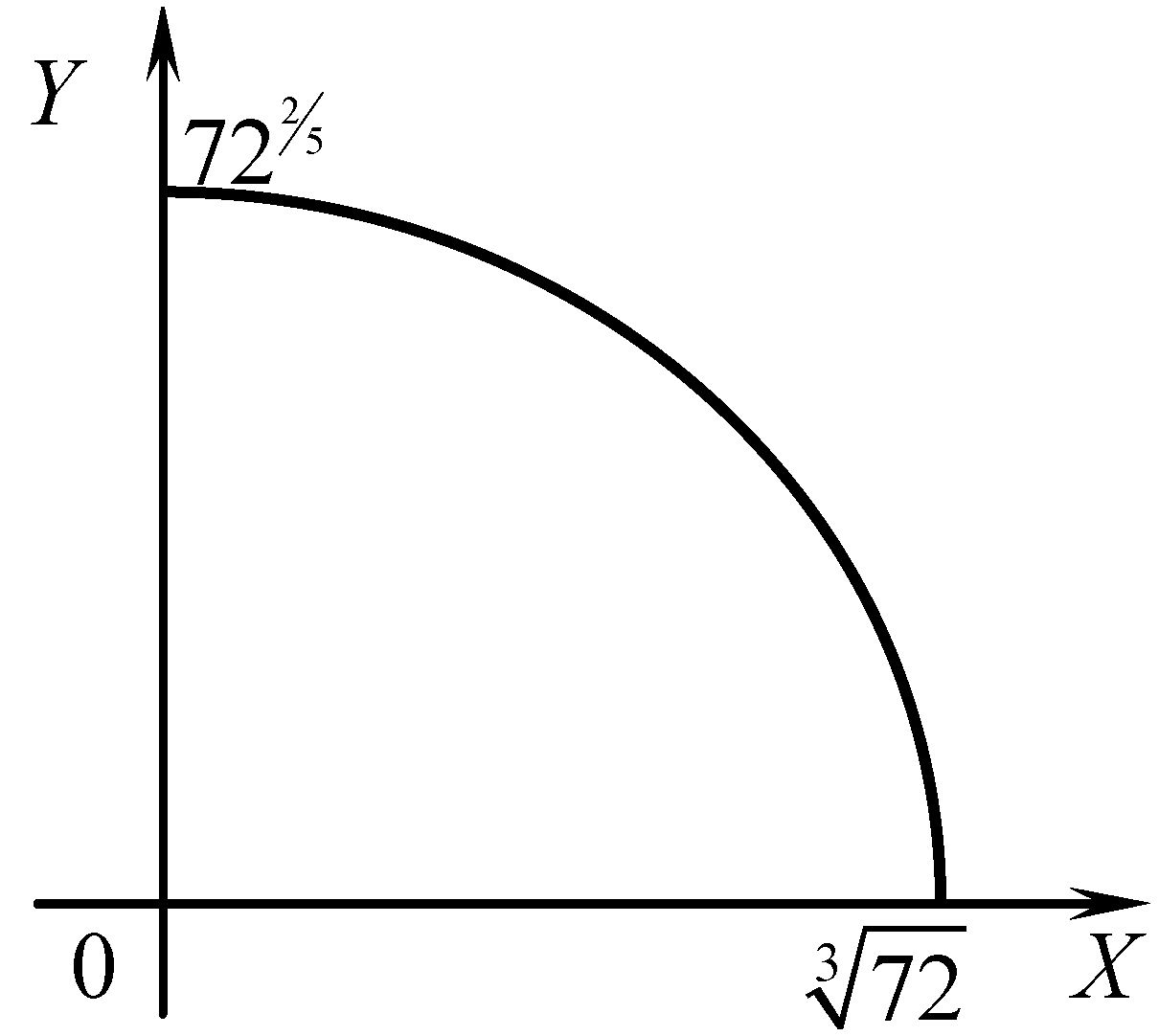
Рис. 15