
эконометрика шпор
.docxЭконометрика – бұл: Математикалық және статистикалық әдістер мен үлгілердің көмегімен экономикалық объектілер мен үрдістердің нақты сандық және сапалық өзара байланыстарын оқытатын ғылым |
||||||||||||
Эконометрика термині екі сөзді біріктіреді: Экономика және метрика |
||||||||||||
Эконометрика – келесі үш құрауыштардың негізінде пайда болған ғылым: Экономикалық ілім, статистика, математикалық әдістер |
||||||||||||
«эконометрика» термині қай жылы енгізілді: 1926 |
||||||||||||
"эконометрика" терминін қай ғалым енгізді: Рагнар фриш |
||||||||||||
"эконометрика" термині тура мағынада келесіні білдіреді: экономикалық өлшеу |
||||||||||||
Эконометриканың базалық ұғымдары: Объект, айнымалы, үлгі |
||||||||||||
Эконометрикалық үлгілердің келесі үш тобын ерекшелеуге болады: Уақыт қатарлары үлгілері, бір теңдеуі бар регрессиялық үлгілер, бірқалыпты теңдеулер жүйелері |
||||||||||||
Экономикалық үрдістерді үлгілеу кезінде келесі мәліметтер типтері қолданылады: Кеңістіктік мәліметтер, уақыт қатарлары, панельдік мәліметтер |
||||||||||||
Айнымалы – бұл: Объектінің шаруашылық әрекеті үрдісінде әр түрлі мәндер қабылдай алатын объектінің сандық сипаттамасы |
||||||||||||
Экономикалық объект – бұл: Кез келген шаруашылық бірлігі |
||||||||||||
Эконометрикалық үлгі – бұл: Объектінің барлық айнымалыларын біріктіріп байланыстыратын графиктер немесе кестелер жиыны, не болмаса математикалық теңдеулер немесе теңсіздіктер жүйесі |
||||||||||||
Уақыт қатарлары үлгілеріне төмендегілер жатады: Тренд үлгілері, маусымдық, тренд және маусымдық үлгілері |
||||||||||||
Эконометриканың әдістерінің біріне келесісі жатады: Уақытша қатарларын талдау |
||||||||||||
Р. Фриш анықтамасы: эконометрика - бұл: Математикалық әдістер мен үлгілердің көмегімен экономикалық объектілердің айнымалылары арасындағы нақты сандық заңдылықтар мен байланыстарды оқытатын экономиканың бір бөл |
||||||||||||
Р. Фриш эконометрика келесі үш құрауыштардың бірлігі екендігін атап Макроэкономика, микроэкономика, статистика |
||||||||||||
Кеңістіктік мәліметтер - бұл:Әр түрлі экономикалық объектілер бойынша бір уақыт мезетінде алынған мәліметтер |
||||||||||||
Панельдік мәліметтер - бұл: Бірнеше уақыт кезеңдерінде әр түрлі экономикалық объектілер бойынша алынған мәліметтер жиынтығы |
||||||||||||
Уақыт қатарлары - бұл:Әр түрлі кезеңдер немесе уақыт мезеттеріндегі бір экономикалық параметрді бақылау |
||||||||||||
Р. Фриш ... Экономисті және статисті, нобель сыйлығының лауреаты Норвегиялық |
||||||||||||
Эконометриканың тура анықтамасын көрсетіңіз: Шынайы статискалық мәліметтердің негізінде шынайы экономикалық құбылыстардың математикалық үлгілерін жетілдіретін және талдайтын ғылым |
||||||||||||
Эконометрикалық зерттеудің негізгі мақсаты: Шынайы әлеуметтік-экономикалық үрдістерді сипаттау, талдау және болжамдау үшін модель құрастыру |
||||||||||||
Эконометриканың міндеттері: Экономикалық үлгілерді құрастыру және олардың параметрлерін бағалау, экономикалық көрсеткіштер мен олардың байланыс түрлерінің қасиеттерінің гипотезаларын тексеру |
||||||||||||
Эконометриканың негізгі мәселесі: Үлгіні құрастыру, шынайы әлеуметтік-экономикалық үрдістерді сипаттау, талдау және болжамдау үшін оның мүмкіндіктерін анықтау |
||||||||||||
Эконометрикалық зерттеу неше кезеңнен тұрады:4 |
||||||||||||
Эконометрикалық үлгінің табылған параметрлерінің сапасын тексеру ... Кезеңі деп аталады:Верификациялау |
||||||||||||
Ковариацияның келесі түрлерін ажыратады: Теориялық және таңдамалы |
||||||||||||
Кездейсоқ шамалардың сандық сипаттамаларын атаңыз: Математикалық күту, дисперсия, орташа квадраттық ауытқу |
||||||||||||
Нөлдік болжам дегеніміз: Тексеруге ұшырайтын болжам |
||||||||||||
Дисперсия қасиеттерінің бірін көрсетіңіз:D(c)=0 |
||||||||||||
Дисперсия қасиеттерінің бірін көрсетіңіз:D(k*x)=k2*d(x) |
||||||||||||
Математикалық күтудің қасиеттерінің бірін көрсетіңіз:М(k*x)=k*м(x) |
||||||||||||
Математикалық күтудің қасиеттерінің бірін көрсетіңіз:M(c)=c |
||||||||||||
Корреляцияның таңдамалы коэффициенті келесі формуламен анықталады
|
||||||||||||
Корреляцияның теориялық коэффициенті келесі формуламе анықталады:
|
||||||||||||
Корреляцияның таңдамалы коэффициенті келесі аралықта анықталады:
|
||||||||||||
Корреляцияның теориялық коэффициенті келесі аралықта анықталады:
|
||||||||||||
X және y кездейсоқ шамалары корреляцияланған деп аталады, егер:P=0 |
||||||||||||
X
және
y
кездейсоқ
шамалары корреляцияланбаған деп
аталады, егер: |
||||||||||||
|
||||||||||||
Орташа квадраттық ауытқуды |
||||||||||||
Дисперсияны |
||||||||||||
А оқиғасының пайда болу ықтималдығы |
||||||||||||
Кездейсоқ шаманың таралу заңын қалай беруге болады: Кестелік, графиктік, аналитикалық |
||||||||||||
Таралу қатарының графиктік бейнеленуі ... Деп атала Таралу полигоны |
||||||||||||
Корреляцияның жұпты коэффициенттерін microsoft excelдің келесі функциясы көмегімен анықтауға болады:Коррел |
||||||||||||
Матрицаларды көбейтуде ms excel бағдарламасының қай функциясы қолданылады Мумнож |
||||||||||||
Матрицаны транспонирлеу үшін қолданылатын ms excelдің кірістірілген функциясы:Трансп |
||||||||||||
5-баған және 9-жолдан тұратын а матрицасы берілген. Оны транспонирлегенде қандай матрица алынады? 9 баған және 5 жолдан тұратын матрица |
||||||||||||
Функцияның максимум және минимумдерін анықтауда қолданылатын ms excel алгоритмі:Поиск решения |
||||||||||||
Бақыланатын мәліметтер бойынша орташа мәнді анықтауға арналған ms excel бағдарламасының функциясы:Срзнач |
||||||||||||
Бақыланатын мәліметтердің қосындысын анықтайтын ms excel бағдарламасының функциясы:Сумм |
||||||||||||
Кері матрицаны есептеуде қолданылатын ms excel математикалық функциясы:Мобр |
||||||||||||
Матрицаның анықтауышын есептеуде қолданылатын ms excel математикалық функциясы:Мопред |
||||||||||||
Формуланы көшірмелегенде сілтеме тұрақты болу үшін қолданылатын функционалдық перне:F4 |
||||||||||||
Теңдеудің түбірлерін анықтауда қолданылатын ms excel бағдарламасының алгоритмі:Подбор параметра |
||||||||||||
Трансп функциясы ms excel-дің кірістірілген функцияларынның келесі категориясына жатады:Ссылки и массивы |
||||||||||||
Келесі мәліметтер бойынша х кездейсоқ шамасының математикалық күтуін есептеңіз:
4,7 |
||||||||||||
Келесі мәліметтер бойынша х кездейсоқ шамасының математикалық күтуін есептеңіз:
|
||||||||||||
Келесі мәліметтер бойынша х кездейсоқ шамасының математикалық күтуін есептеңіз:
9,95 |
||||||||||||
Келесі мәліметтер бойынша х кездейсоқ шамасының математикалық күтуін есептеңіз:
7,6 |
||||||||||||
Z = 8х – 5у + 7 кездейсоқ шамасының математикалық күтуін, дисперсиясын және орташа квадраттық ауытқуын табыңыз, егер м(х) = 3, м(у) = 2, d(x) = 1,5, d(y) = 1, мұндағы м(х) және м(у) - х және у математикалық күтулері, d(x) және d(y) – х және у дисперсиялары 21;121;11 |
||||||||||||
Z = 8х – 5у + 7 кездейсоқ шамасының математикалық күтуін, дисперсиясын және орташа квадраттық ауытқуын табыңыз, егер м(х) =4, м(у) = 3, d(x) = 2, d(y) = 1,5 болса, Мұндағы м(х) және м(у) - х және у математикалық күтулері, d(x) және d(y) – х және у дисперсиялары 424; 165,5; 12,86 |
||||||||||||
Z = 8х – 5у + 7 кездейсоқ шамасының математикалық күтуін, дисперсиясын және орташа квадраттық ауытқуын табыңыз, егер м(х) =2, м(у) = 1, d(x) = 1, d(y) = 0,5 болса, Мұндағы м(х) және м(у) - х және у математикалық күтулері, d(x) және d(y) – х және у дисперсиялары18; 76,5; 8,74 |
||||||||||||
Z = 4х – 5у + 3 кездейсоқ шамасының математикалық күтуін, дисперсиясын және орташа квадраттық ауытқуын табыңыз, егер м(х) =4, м(у) = 3, d(x) = 2, d(y) = 1,5, Мұндағы м(х) және м(у) - х және у математикалық күтулері, d(x) және d(y) – х және у дисперсиялары4; 69,5; 8,33 |
||||||||||||
Сызықты регрессияның детерминация коэффициенті мынаған тең: Корреляция коэффициентінің квадраты |
||||||||||||
Детерминация коэффициенті r2 есептеңіз, егер корреляция коэффициенті r=0,61 болса0,3721 |
||||||||||||
Детерминация коэффициенті r2 есептеңіз, егер корреляция коэффициенті r=0,7 болса0,49 |
||||||||||||
Детерминация коэффициенті r2 есептеңіз, егер корреляция коэффициенті r=0,9 болса0,81 |
||||||||||||
Детерминация коэффициенті r2 есептеңіз, егер корреляция коэффициенті r=0,57 болса:0,325 |
||||||||||||
Регрессия теңдеуінің коэффициентіФактор 1 бірлікке өзгергенде нәтижесі қанша бірлікке өзгеретінінкөрсетеді |
||||||||||||
Гомоскедастикалылық дегеніміз: Ауытқу дисперсиясының тұрақтылығы |
||||||||||||
Гетероскедастикалылық дегеніміз: Ауытқу дисперсиясының тұрақсыздығы |
||||||||||||
Гетероскедастикалылық мәселесі көбінесе ... Тән: Кеңістіктік мәліметтерге |
||||||||||||
Гетероскедастикалылықты болдырмау үшін ... Қолданады: Өлшенген квадраттар әдісін |
||||||||||||
Гетероскедастикалылықты анықтау үшін төмендегілер қолданылады: Ауытқулардың графикалық талдауы, спирменнің рангілік корреляция тесті, парк тесті, глейзер тесті, голдфелд-квандт тесті |
||||||||||||
Гомоскедастикалылық |
||||||||||||
шартының орындалмауы ... Аталады: Гетероскедастикалылық |
||||||||||||
Түзу үшін модельдеу қателігін есептеу формуласы:
|
||||||||||||
Парабола үшін модельдеу қателігін есептеу формуласы:
|
||||||||||||
Сызықты тәуелділік – ... Арасындағы тәуелділік Екі корреляцияланған белгілер |
||||||||||||
Түзудің коэффициенттерін анықтау үшін келесі формуланы қолданамыз:
|
||||||||||||
Парабола
коэффициенттерін анықтау үшін келесі
формуланықолданамыз: |
||||||||||||
Детерминация коэффициентін есептеу формуласы:
|
||||||||||||
Корреляция
индексін есептеу формуласы: |
||||||||||||
Ең
кіші квадраттар әдісінің формуласы: |
||||||||||||
Жұпты
корреляцияның сызықты коэффициенті
|
||||||||||||
Регрессияның келесі түрлерін ажырата:Сызықтық және сызықтық емес |
||||||||||||
Сызықты
емес регрессия үшін корреляция
индексі
|
||||||||||||
Детерминация коэффициентін анықтау формуласы:
|
||||||||||||
Аппроксимацияның орташа қателігін анықтау формуласы:
|
||||||||||||
Икемділік
коэффициентін есептеу формуласы: |
||||||||||||
Көптік регрессия теңдеуінің параметрлерін бағалау үшін қолданады: Ең кіші квадраттар әдісін |
||||||||||||
Транспорттық есептің мақсаты ... Болып табылады: тасымалдау тарифтерін азайту; |
||||||||||||
Транспорттық есепті ... Көмегімен шешуге болады: «поиск решения» алгоритмі |
||||||||||||
Модельдеу қателігін анықтау үшін қай формула қолданылады?
|
||||||||||||
Жүйелік
дисперсия: |
||||||||||||
Модельдік
дисперсия: |
||||||||||||
Эконометрикалық модельдің құрылуының негізіне қандай сараптамалар жатады:Корреляциялық-регрессиялық |
||||||||||||
Регрессия б:Зерттеуші экономикалық көрсеткіштер аралық әдіс есебі |
||||||||||||
Корреляция бұл: Зерттеуші экономикалық көрсеткіштердің арасындағы байланыс түр |
||||||||||||
Қалдық
дисперсия: |
||||||||||||
Эконометриканың математикалық құрылғысы қандай? Математикалық және қосымша статистикалық тәсіл |
||||||||||||
Моделдеуге қандай факторлар жатады?Сапалы және сандық; |
||||||||||||
Кобба-дугластың өндірістік функциясында параметрі қандай коэффициентке сәйкес келеді:Икемділік |
||||||||||||
Классикалық үлгінің алғышарты болмайтын болжамды табыңыз. Кездейсоқ ауытқудың нормальданған үлестірімі болмайды |
||||||||||||
Стьюдент критериінің кестелік мәні келесі шамаларға тәуелді Сенімділік ықтималдығына да, факторлар санына да, берілген қатардың ұзындығана да |
||||||||||||
Қайсы регрессия теңдеуі сызықтық түрге келтірілмейді?
|
||||||||||||
Теңдеулердің
қайсысы дәрежелік болып табыла |
||||||||||||
Жұптық регрессияны көптік регрессия орнына қолдану мысалы болып табылатыны қайсысы:Спецификация қателіктері |
||||||||||||
Жалпы алғанда регрессия теңдеуінің маңыздылығын бағалау келесі шама көмегімен алынады:F – фишер критериі |
||||||||||||
Автокорреляция дегеніміз не? Регрессия қалдықтарының өзара тәуелділігі |
||||||||||||
Дарбин-уотсон критериі не үшін қолданылады?4 Қалдықтар автокорреляциясының үлгісін тексеру үшін |
||||||||||||
Гетероскедастикалықтың мағынасы неде? Кездейсоқ ауытқулардың дисперсиясы өзгереді |
||||||||||||
Уақыт қатарларының деңгейі келесілерден тұруы мүмкін: Тенденция, циклдік, маусымдық, кездейсоқ тербелістердің кез келген |
||||||||||||
Детерминация
коэффициентінің
Регрессия теңдеуімен түсіндірілген у мәндерінің жалпы шашырату бөлігін анықтайтын коэффициент |
||||||||||||
Мультиколлинеарлық – бұл: Екі немесе бірнеше айнымалылардың өзара сызықтық байланысы |
||||||||||||
Мультиколлинеарлықты анықтау белгілерінің бірі: Корреляцияның меншікті коэффициенттерінің жоғары болуы |
||||||||||||
Мультиколлинеарлықты жою әдістерінің бірі: Үлгінің спецификациясын өзгерту |
||||||||||||
Кездейсоқ шаманы тұрақты санға көбейтсе, оның дисперсиясы:; Сол санның квадратына көбейтіледі; |
||||||||||||
Кездейсоқ шаманың дисперсиясы: Кездейсоқ шама мен оның математикалық үмітінің айырымының квадратының математикалық үмітіне тең |
||||||||||||
Стандартты
қалыпты үлестірудің параметрлерін
көр |
||||||||||||
Егер эконометриялық модельде тек қана бір түсіндіруші айнымалы болса, онда ол былай аталадыЖұптық регрессия; |
||||||||||||
Дискретті
кездейсоқ шама
|
||||||||||||
20 күн ішінде алынған күнделікті сатылатын тауарлардың көлемі берілген: 5, 6, 2, 3, 7, 7, 6, 6, 10, 11, 6, 10, 11, 6, 4, 5, 6, 4, 5, 6. Таңдаманың орташасын есептеңіз.6,3 |
||||||||||||
Жұптық
сызықтық регрессияның теңдеуін
көрсетіңіз: |
||||||||||||
кездейсоқ шамасының үлестіру кестесі берілген.
 анықтаңыз6,44
анықтаңыз6,44
|
||||||||||||
- кездейсоқ шаманың үлестіру кестесі берілген Табу
керек:
13.8; |
||||||||||||
X және y шамаларының арасындағы байланыс неғұрлым тығыз болса, соғұрлым детерминация коэффициенті қандай санға жақын болады 1; |
||||||||||||
Құрылған моделдің сапасын қай көрсеткіш анықтайды? Детерминация коэффициенті; |
||||||||||||
Бас жиынның үлестіру параметрлерінің шамалары туралы жорамал қалай аталады?Статистикалық болжам; |
||||||||||||
|
||||||||||||
Регрессия теңдеуінде екі немесе бірнеше түсіндіруші айнымалылар арасындағы тығыз корреляциялық байланыс қалай аталады Мультиколлинеарлық; |
||||||||||||
Жұптық
сызықтық регрессия параметрі
|
||||||||||||
Дұрыс тұжырымды таңдаңыз: Детерминация
коэффициентінің статистикалық
маңыздылығын тексеру үшін стьюденттің
|
||||||||||||
17 бақылаудан тұратын таңдама бойынша жұптық сызықтық регрессияда - статистиканың кризистік мәнін табу үшін қандай еркіндік дәрежесін қолдану керек15; |
||||||||||||
Бір
айнымалы
Модельге кірмеген факторлардың әсерін көрсететін кездейсоқ шама. |
||||||||||||
Егер
х кездейсоқ шама болмаса, онда
гаусс-марковтың кездейсоқ ауытқу
түсіндіруші айнымалылардан тәуелсіз
болу шарты келесі формуламен жазылады |
||||||||||||
Егер
және
|
||||||||||||
Нөлдік
гипотеза ( |
||||||||||||
Кездейсоқ ауытқу қалыпты үлестірілген туралы болжам неге негізделген: Гаусс-марков теоремасына; |
||||||||||||
Келтірілген көрсеткіштердің қайсысы және айнымалыларының бірлік өлшемдеріне тәуелді: және айнымалыларының ковариация коэффициенты |
||||||||||||
Егер
және
сызықтық
регрессия теңдеулері есептелген
болса, онда
Корреляция коэффициентінің квадратына. |
||||||||||||
Егер
сызықтық регрессия теңдеуінің бос
мүшесінен басқа коэффициенттері нөлге
тең болса, онда:Регрессия
теңдеуі
|
||||||||||||
Екінші текті қате жіберу себебі: Но болжамын қабылдаймыз, бірақ негізінде н1 болжамы дұрыс. |
||||||||||||
Кез
келген бақылаулар үшін кездейсоқ
ауытқу
|
||||||||||||
Барлық бақылауда кездейсоқ мүшенің дисперсиясы тұрақты болуын қажет етеді: Гаусс-марков теоремасы; |
||||||||||||
Бірінші текті қате жіберу себебі: Дұрыс
нөлдік болжам
|
||||||||||||
Барлық бақылаулар үшін кездейсоқ ауытқулардың математикалық күтулері нөлге тең болу шартын қажет етеді:Гаусс-марков теоремасы; |
||||||||||||
Қалыпты
үлестірілген кездейсоқ шаманың (
|
||||||||||||
Бас жиынның дисперсиясының жылжыған бағасы Түзетілген таңдаманың дисперсиясы; |
||||||||||||
Төрт қос бақылау нәтижесінде келесі қосындылар берілген
Табу
керек
|
||||||||||||
Регресия
теңдеуі берілген Табу
керек
|
||||||||||||
1; |
||||||||||||
Келесі формуламен қандай көрсеткіш есептеледі?
Корреляция коэффициенті; |
||||||||||||
Детерминация
коэффициентінің маңыздылығын бағалау
үшін қандай критерий колданылады?Фишердің
|
||||||||||||
Бірінші текті қате жібермеу ықтималдығы; |
||||||||||||
Гетероскедастық келесі шарт орындалмау нәтижесінде пайда болады Гетероскедастық регрессия коэффициенттерін бағалауда әсеретпейді. |
||||||||||||
|
||||||||||||
|
||||||||||||
Стьюдент үлестіруі қай гипотезаны тексеруде қолданылмайды? Бірінші ретті автокорреляция жоқ; |
||||||||||||
Мультиколлинеарлық
шарт орындалмайтын регрессия теңдеуін
көрсет: (
|
||||||||||||
-
статистика келесі формуламен анықталады
(
-бақылау
саны;
|
||||||||||||
Стандартталған
масштабтағы көптік регрессия теңдеуі
келесі түрде болады: |
||||||||||||
Стандартталған
масштабтағы көптік регрессия теңдеуінде
a
параметрі
төмендегідей анықтала |
||||||||||||
Көптік
регрессия теңдеуін құрастыруда
қолданылатын дәрежелік функцияны
көрсетіңіз: |
||||||||||||
Көптік
регрессия теңдеуін құрастыруда
қолданылатын сызықтық функцияны
көрсет |
||||||||||||
Ms excel бағдарламасының линейн кірістірілген функциясы нені анықтайды:Y=a+bx регрессия теңдеуінің параметрлерін |
||||||||||||
Ms
excel
бағдарламасының қандай статистикалық
функциясы,
|
||||||||||||
Ms
excel
бағдарламасының қандай статистикалық
функциясы,
|
||||||||||||
Отрезок, наклон, предсказ, стошух функциялары ms excel бағдарламасының кірістірілген функцияларының қайсы категориясына жатады?Статистические |
||||||||||||
Құрылған модельдің сапасы жақсы деп есептеледі, егер орташа қатенің апроксимациясы келесі аралықта жататын болса8-10%; |
||||||||||||
Кез
келген бақылаулар үшін
|
||||||||||||
Бақылаулар кестесі берілген
Корреляция
коэффициентін есептеңіз |
||||||||||||
Үш қос бақылау нәтижесінде келесі қосындылар берілген
|
||||||||||||
|
||||||||||||
Бақылаулар кестесі берілген
Y=b0+b1x регрессия теңдеуін жаз.Y=1+x |
||||||||||||
Бақылаулар кестесі берілген
Корреляция коэффициентін есептеңіз . |
||||||||||||
Төрт қос бақылау нәтижесінде келесі қосындылар берілген
|
||||||||||||
Төрт қос бақылау нәтижесінде келесі қосындылар берілген
Детерминация
коэффициентін табыңыз |
||||||||||||
Егер
бақылаулар саны 3 және
|
||||||||||||
және
|
||||||||||||
және
айнымалыларының
қос сызықтық регрессия коэффициенті
-
ді анықтаңыз, ег 0.72; |
||||||||||||
Нөлдік
гипотеза (
)
тексергенде қос сызықтық регрессияның
- статистика мәні табылды
|
||||||||||||
Қос
сызықтық регрессияның 30 бақылау
бойынша
параметрін анықтаңыз, егер
81; |
||||||||||||
Жиырма
бақылау бойынша жұптық
сызықтық регрессияның
12; |
||||||||||||
Келесі формула бойынша есептелетін көрсеткіш
Бірінші текті автокорреляция коэффициенті; |
||||||||||||
Келесі болжамды тексеру үшін
Қолданылатын - статистиканы көрсет ( -бақылау саны; - түсіндіруші айнымалылар саны) |
||||||||||||
Келесі формула бойынша есептелетін көрсеткіш
Дарбин-уотсон статистикасы. |
||||||||||||
Келесі статистика бойынша тексерілетін болжамды көрсет:
Корреляция коэффициентінің маңыздылығы туралы; |
||||||||||||
22 бақылаулар нәтижесінде келесі мәліметтер алынған:
Түзетілген детерминация коэффициентін, икемділіктің меншікті коэффициенттерін, a параметрінің мәндері неге тең:
|
||||||||||||
Y-тің x1 және х2 қатысты регрессия теңдеуінің стандартталған және табиғи масштабтағы теңдеулері келесі түрде болады:
|
||||||||||||
15 кәсіпорын жиынтығынан а тауары мен х бағасы және у табыс пен сауда кәсіпорны арасындағы тәуелділік зерттеледі. Регрессиялық үлгіні бағалауда келесі нәтижелер алынды:
Корреляция индексі мен f-критерийдің нақты мәні анықтаңыз.
|
||||||||||||
18 кәсіпорын жиынтығынан а тауары мен х бағасы және у табыс пен сауда кәсіпорны арасындағы тәуелділік зерттеледі. Регрессиялық үлгіні бағалауда келесі нәтижелер алынды:
Корреляция индексі мен f-критерийдің нақты мәні анықтаңыз.
|
||||||||||||
25 кәсіпорын жиынтығынан а тауары мен х бағасы және у табыс пен сауда кәсіпорны арасындағы тәуелділік зерттеледі. Регрессиялық үлгіні бағалауда келесі нәтижелер алынды:
|
||||||||||||
20 кәсіпорын жиынтығынан а тауары мен х бағасы және у табыс пен сауда кәсіпорны арасындағы тәуелділік зерттеледі. Регрессиялық үлгіні бағалауда келесі нәтижелер алынды:
Корреляция индексі мен f-критерийдің нақты мәні анықтаңыз.
|
||||||||||||
30 кәсіпорын жиынтығынан а тауары мен х бағасы және у табыс пен сауда кәсіпорны арасындағы тәуелділік зерттеледі. Регрессиялық үлгіні бағалауда келесі нәтижелер алынды:
Корреляция индексі мен f-критерийдің нақты мәні анықтаңыз.
|
||||||||||||
20 кәсіпорын жиынтығынан а тауары мен х бағасы және у табыс пен сауда кәсіпорны арасындағы тәуелділік зерттеледі. Регрессиялық үлгіні бағалауда келесі нәтижелер алынды:
Корреляция индексі мен f-критерийдің нақты мәні анықтаңыз.
|
||||||||||||
15 кәсіпорынның концерні бойынша у сату көлемі х жарнамасына тәуелділігі келесі түрде сипатталады: к Rxy=0,90 |
||||||||||||
16 кәсіпорнының концерні бойынша у сату көлемі х жарнамасына тәуелділігі келесі түрде сипатталады Корреляция коэффициентін анықтаңыз.Rxy=0,84 |

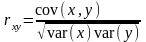



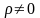
 -
бұл
... Формуласы
Математикалық
күтуді есептеу
-
бұл
... Формуласы
Математикалық
күтуді есептеу - бұл
... Есептеу формуласы
- бұл
... Есептеу формуласы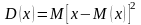 - бұл
... Есептеу формуласы
- бұл
... Есептеу формуласы шартының
орындалуы ... Деп аталады:
шартының
орындалуы ... Деп аталады: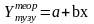






 келесі
аралықта анықталады:
келесі
аралықта анықталады:
 келесі
аралықта анықталады:
келесі
аралықта анықталады: :
:

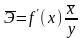




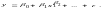

 маңызы
келесіден тұрады:
маңызы
келесіден тұрады: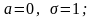
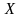 -
тің математикалық күтуі
қай формуламен есептеледі?
-
тің математикалық күтуі
қай формуламен есептеледі?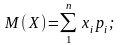


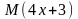
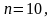


 ,
болса таңдаманың ковариация коэффициенті
қандай мән қабылдайды?
,
болса таңдаманың ковариация коэффициенті
қандай мән қабылдайды?
 ең кіші квадраттар әдісі бойынша
келесі формуламен анықталады
ең кіші квадраттар әдісі бойынша
келесі формуламен анықталады
 -
статистикасы қолданылады;
-
статистикасы қолданылады; және
және
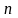 түсіндіруші айнымалысы бар экономикалық
моделде
түсіндіруші айнымалысы бар экономикалық
моделде
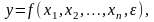
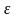 -
мүшесі:
-
мүшесі:

 -тің
орташа мәндері сәйкесінше 18 және 4.75,
ал
-тің
орташа мәндері сәйкесінше 18 және 4.75,
ал
 коэффициенті 2-ге тең болса,
-тің
-ке
регрессия теңдеуі қандай?
коэффициенті 2-ге тең болса,
-тің
-ке
регрессия теңдеуі қандай? .
.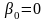 )
тексергенде жұптық сызықтық регрессияның
- статистика мәні табылды
)
тексергенде жұптық сызықтық регрессияның
- статистика мәні табылды
 стандартты қатесі 0.001 болса,
коэффициентін анықтаңыз
=0.024;
стандартты қатесі 0.001 болса,
коэффициентін анықтаңыз
=0.024; және
және
 коэффициенттерінің көбейтіндісі неге
тең:
коэффициенттерінің көбейтіндісі неге
тең: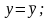
 дисперсиясы бірдей болуы қалай
аталады?Гомоскедастық;
дисперсиясы бірдей болуы қалай
аталады?Гомоскедастық;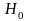 жоққа шығарылады;
жоққа шығарылады;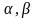 )
интервалында мән қабылдау ықтималдығы
қай формуламен анықталады.
)
интервалында мән қабылдау ықтималдығы
қай формуламен анықталады.


 ;
;

 ;
;
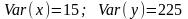 .
Табу керек
.
Табу керек

 -статистикасы
-статистикасы маңыздылық деңгейі
деп нені атайды?
маңыздылық деңгейі
деп нені атайды?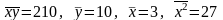 белгілі болса,
қос сызықтық регрессия теңдеуінің
параметрінің мәнін табыңыз
белгілі болса,
қос сызықтық регрессия теңдеуінің
параметрінің мәнін табыңыз
 болса, 30 бақылау
нәтижесі бойынша бағаланған қос
сызықты регрессияның
параметрін анықтаңыз
болса, 30 бақылау
нәтижесі бойынша бағаланған қос
сызықты регрессияның
параметрін анықтаңыз
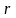 -
корреляция коэффициенті)
-
корреляция коэффициенті)
 - түсіндіруші айнымалылар саны)
- түсіндіруші айнымалылар саны)

 ;.
;. ;
; ;
; коэффициентін
есептейді:Отрезок
коэффициентін
есептейді:Отрезок коэффициентін
есептейді:Наклон
коэффициентін
есептейді:Наклон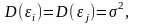
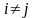 шарттың
орындалуы қалай аталады?Гомоскедастық;.
шарттың
орындалуы қалай аталады?Гомоскедастық;.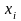

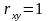 ;
;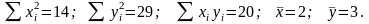
 регрессия теңдеуін
жаз.
регрессия теңдеуін
жаз. .
.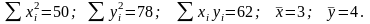 регрессия теңдеуін
жаз.
;
регрессия теңдеуін
жаз.
;


 ;.
;.

 болса, таңдаманың ковариация
коэффициенті неге тең
болса, таңдаманың ковариация
коэффициенті неге тең
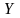 айнымалыларының
қос сызықтық регрессия коэффициенті
айнымалыларының
қос сызықтық регрессия коэффициенті
 ,
орташа мәндері 30.5 және 5.75 болса, оның
регрессия теңдеуі қандай ?
,
орташа мәндері 30.5 және 5.75 болса, оның
регрессия теңдеуі қандай ? ;
;
 .
Стандарттық қатесі 0.001 болса,
коэффициентін анықтаңыз0.036;
.
Стандарттық қатесі 0.001 болса,
коэффициентін анықтаңыз0.036;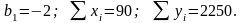
 статистикасын
анықтаңыз, егер
статистикасын
анықтаңыз, егер
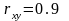




 ,
,
 ;
;
 ;
;
 ;
;
 ;
;
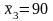





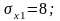

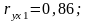



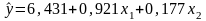


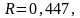



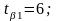



 Корреляция
индексі мен f-критерийдің нақты мәні
анықтаңыз.
Корреляция
индексі мен f-критерийдің нақты мәні
анықтаңыз.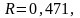
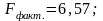
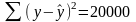
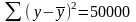
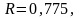







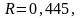
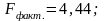
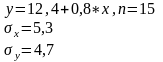 орреляция
коэффициентін анықтаңыз.
орреляция
коэффициентін анықтаңыз.