10 Законы изменения и сохранения момента импульса системы

Закон изменения момента импульса.

 

Рассмотрим произвольную систему тел. Моментом импульса системы назовем величину L, равную векторной сумме моментов импульсов отдельных ее частей L_i, взятых относительно одной и той же точки выбранной системы отсчета.

                                            L = ΣL_i.                                                           

Найдем скорость изменения момента импульса системы. Проведя рассуждения, аналогичные описанию вращательного движения твердого тела, получим, что

скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

                                     dL/dt = M.                                                      

Причем вектора L и M задаются относительно одной и той же точки O в выбранной СО. Уравнение (21) представляет собой закон изменения момента импульса системы.

Причиной изменения момента импульса является действующий на систему результирующий момент внешних сил. Изменение момента импульса за конечный промежуток времени можно найти, воспользовавшись выражением

                                      .                                           

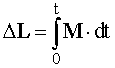Приращение момента импульса системы равно импульсу результирующего момента внешних сил, действующих на нее.

В неинерциальной системе к моменту внешних сил необходимо прибавить момент сил инерции относительно выбранной точки O.

Закон сохранения момента импульса. 

 

Из закона изменения момента импульса, полученного нами для системы тел, вытекает закон сохранения момента импульса применительно к механике:

момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Еще раз подчеркнем, что при использовании этого закона моменты импульса и сил необходимо брать относительно одно и той же оси.

Закон сохранения момента импульса является фундаментальным законом природы и выполняется для любых, а не только механических систем.

Следствия из закон сохранения момента импульса:

        в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;

        если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;

        в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.

Примеры: к первому следствию - при движении человека, находящегося на поверхности диска, по окружности с центром, совпадающим с центром масс диска, последнийначинает

поворачиваться в сторону, противоположную движению человека относительно Земли;  ко второму следствию - ко второму следствию - студент, держащий в вытянутых расправленных руках гантели, сидит на скамье (скамье Жуковского), которая вращается вокруг вертикальной оси. В случае приближения гантелей к груди угловая скорость движения системы “скамья-студент-гантели” увеличивается.

к третьему следствию к третьему следствию - в начальный момент времени студент сидит на неподвижной скамье Жуковского и удерживает в руках раскрученное колесо. Пусть ось вращения колеса перпендикулярна оси вращения Z скамьи Жуковского, т. е. расположена в горизонтальной плоскости. При повороте колеса на 90^о в вертикальной плоскости проекция момента импульса системы “скамья-студент-колесо” на вертикальную ось L_z не изменится и останется равной нулю.

L_z = L_z студ + L_z кол = L_z0 = 0, т.е. L_z студ = - L_z кол.

Следовательно, вектора угловых скоростей системы “студент-скамья” и колеса направлены в противоположные стороны.