Основные понятия и определения

Термическое (характеристическое) уравнение состояние Клапейронадля1кг. Идеального газа имеет вид:

, где: Р - удельное давление (Н/м²);

V - удельный объём (м³/кг);

Т - абсолютная температура(К).

Коэффициент пропорциональности R в уравнении (1) называется газовой характеристической постоянной, величина которой зависит от физической природы газа. При нормальных условиях для воздуха:

молекулярная масса μ=28,96 кг/кмоль

плотность ρ=1,293 кг/м³

объём киломоля Vμ=22,4м³/моль

газовая постоянная R=287 дж/кг_*град

Для выяснения физического смысла газовой постоянной запишем уравнение Клапейрона для двух состояний газа при постоянном давлении (изобарный процесс):

PV₁=RT₁ (2)

PV₂=RT₂ (3)

В ычитая из уравнения (3) уравнение (2) и преобразуя, получим:

Уравнение (4) показывает, что газовая постоянная по своему физическому смыслу является работой, совершаемой 1кг. газа в изобарном процессе при изменении его температуры на 1 градус.

Величина R в уравнении Клапейрона (1) является постоянной для каждого газа в отдельности.

Уравнению (1) можно придать универсальную форму записи, если газовую постоянную отнести не к 1 кг, а к 1 киломолю (молю) газа. Для этого приводим некоторые определения:

Молекулярная масса газа μ (кг/кмоль) – есть численное выражение отношения массы молекулы данного вещества к 1/12 массы атома изотопа углерода ¹²С.

Килограмм- молекула (киломоль, моль)- количество газа, масса которого в килограммах численно равна его молекулярной массе (например, для кислорода моль равен 32 кг, для азота- 28 кг и т.д.). Из закона Авогадро следует, что объём киломоля ( μV=Vμ) при одинаковых физических условиях имеет постоянное значение.

Т огда уравнение состояния для 1 моля газа и выражение R_μ запишутся в виде:

Vμ - объём 1 моля м³/моль

μ - масса киломоля данного газа кг/кмоль

Произведение μR в уравнении (6) называется универсальной газовой постоянной и по физическому смыслу является работой 1 киломоля идеального газа в изобарном процессе при изменении его температуры на 1 градус.

Для нормальных физических условий численное значение универсальной газовой постоянной в технической и СИ системах измерения будут одинаковы для всех газов и равны соответственно:

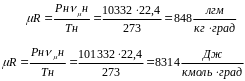
Индивидуальная газовая постоянная в двух системах измерения, отнесенная к 1 кг газа при этом будет равной:

Тогда универсальное уравнение состояния запишется в виде:

PV_μ=848 TМКГСС; PV_μ=8314 TСИ (7)

Vμ - объём моля;

μ - масса киломоля газа.

Уравнение (7) называют уравнением Клапейрона – Менделеева, т.к. оно впервые было предложено Менделеевым в 1874 г.

Описание опытной установки.

Воздушным компрессором 1 воздух нагнетается в тонкостенный металлический сосуд 2. Давление воздуха в сосуде контролируется

м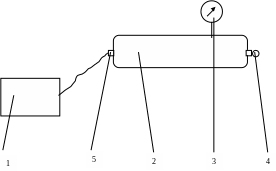 анометром 3.Сосуд снабжён клапаном 4 для выпуска воздуха и клапаном 5 – для впуска.

Для контроля веса сосуда используются весы.