№20 (Форвард)Туркина
Дано:
T₁=10
T₂=4
Решение:
1)
Берём займ M₀ под
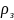на T₁:
.
2)
Делаем вклад в банк под
на T₂.
3) Покупаем форвард на T₁-T₂.
займ на весь срок
0
4
10
форвард
вклад
– займ
– вклад
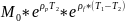– сколько получим
– прибыль
Задача 21 Астраханцева Александра У05-721Б)
Дано:
Мы владеем бизнесом, который имеет такой поток платежей
7 12 6
0 1,5 3 4,5
10
Известно что з=10%; р=8%. Но появилась возможность сдать офисные помещения в аренду, при условии непрерывно начисляемой ставке ренты =0,04 и ежемесячных выплатах m=12.
Найти:
Необходимо выяснить при какой арендной ставке нам это выгодно.
Решение:
Рассчитаем NTV и NPV бизнеса
ti |
Ci |
NTV=Ci*(e^(p*(Т-t)) |
NPV=NTV*(e^(-p*T)) |
0 |
-10 |
-17,16006862 |
-10 |
1,5 |
7 |
8,898744052 |
6,208443057 |
3 |
12 |
13,52996222 |
9,439534333 |
4,5 |
6 |
6 |
4,186057956 |
Total |
|
11,27 |
9,9 |
Найдем NTVренты
Подставим значения
Чтобы сдача помещений в аренду была выгодна должно соблюдаться неравенство
ОТВЕТ: Если ставка аренды будет выше 0,2 , то сдача офисов будет выгодна
Задача 22. (Хусаинова Даша)
Дано:
Современная стоимость ренты С1 -? Непрерывное начисление стоимости по выплатам α1 – 7%. Т1= 20, выплаты производятся ежемесячно. Количество квартир N = 50.
С2 - ? α2 - 6%. Т2=20, выплаты производятся ежеквартально. Ρр = 9%, ρз = 12%
Решение:
NTV1≤NTV2
Ответ: Для получения выгоды мы должны сдавать в 4,5 раза дороже, чем снимать.
Задача №23. (Хусаинова Даша)
Дано:
Дана ипотека на Т - 10 лет с ежемесячным погашением. Ставка по ипотеке R – 13%. Стоимость М равна 12 млн, первый взнос М0 равен 0,3М = 3,6 млн. ρразм = 6%, ρз = 7%. Найти I1,I2,I3, NTV
Решение:
=14,9251869
-17,783269
12,0588989
27,8518323
Ответ: NTV = 27,858; I1=14,9252; I2 = -17,7833; I3 = 12,0589
Задача №24 . (Хусаинова Даша)
3
7
5
0,89
1.5
3.2
1,2
3/4
1
2
10
m=4
R=14%
Расписать потоки платежей.
Решение:
р=m*ln(1+R/m)=4*ln(1+0,14/4)=0,1376
m= |
4 |
R= |
14% |
p= |
0,137605707 |
|
|
|
|
|
|
|
|
|
|
|
I |
t_i^+ |
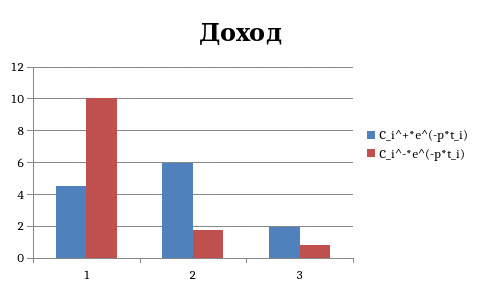
C_i^+ |
C_i^+*e^(-p*t_i) |
C_i^+*e^(-p_i*t)/P_0 |
t_i+*w_i |
t_i^2*w_i |
+ |
1 |
0,75 |
5 |
4,509713528 |
0,364401494 |
0,273301 |
0,204976 |
+ |
2 |
1,2 |
7 |
5,9345031 |
0,479529749 |
0,575436 |
0,690523 |
+ |
3 |
3,2 |
3 |
1,931455815 |
0,156068757 |
0,49942 |
1,598144 |
|
|
|
|
12,37567244 |
1 |
1,348157 |
2,493643 |
|
|
|
|
|
|
V+= |
0,676116 |
|
|
|
|
|
|
|
|
|
I |
t_i^- |
C_i^- |
C_i^-*e^(-p*t_i) |
C_i^-*e^(-p*t_i)/P_0 |
t_i-*w_i |
t_i^2*w_i |
- |
1 |
0 |
10 |
10 |
0,794725113 |
0 |
0 |
- |
2 |
0,89 |
2 |
1,769466523 |
0,140623948 |
0,125155 |
0,111388 |
- |
3 |
1,5 |
1 |
0,813500644 |
0,064650939 |
0,096976 |
0,145465 |
|
|
|
|
12,58296717 |
1 |
0,222132 |
0,256853 |
|
|
|
|
|
|
V-= |
0,20751 |
Задача 26 (Астраханцева Александра У05-721Б)
Найти:
Проанализировать поток выплат. Подсчитать NPV, дюрацию, дисперсию, выпуклость.
Дано:
Имеем поток: ставка =14%
2 6 10 7 5
0 0,6 0,8 1,3 1,6 2 2,2 2,7 3 3,1 3,3
10 5 4 6 2 1
Решение:
Рассчитаем показатели для положительных платедей:
i |
ti |
Ci |
NPV=Ci*(e^(-p*(ti)) |
Ci*(e^(-p*t))/P0=w |
ti*w=D |
(ti^2)*w=G |
1 |
0,6 |
2 |
1,839 |
0,082 |
0,049 |
0,030 |
2 |
1,3 |
6 |
5,002 |
0,223 |
0,290 |
0,377 |
3 |
2,0 |
10 |
7,558 |
0,337 |
0,674 |
1,348 |
4 |
2,7 |
7 |
4,797 |
0,214 |
0,577 |
1,559 |
5 |
3,1 |
5 |
3,240 |
0,144 |
0,448 |
1,388 |
Итог |
30,000 |
22,434 |
1,000 |
2,038 |
4,700 |
|
|
V= |
0,548 |
|
|
|
|
Рассчитаем показатели для отрицательных платежей:
i |
ti |
Ci |
NPV= Ci*(e^(-p*ti)) |
Ci*(e^(-p*t))/P0=w |
ti*w=D |
(ti^2)*w=G |
1 |
0 |
10 |
10,000 |
0,416 |
0,000 |
0,000 |
2 |
0,8 |
5 |
4,470 |
0,186 |
0,149 |
0,119 |
3 |
1,6 |
4 |
3,197 |
0,133 |
0,213 |
0,341 |
4 |
2,2 |
6 |
4,409 |
0,184 |
0,404 |
0,888 |
5 |
3 |
2 |
1,314 |
0,055 |
0,164 |
0,492 |
6 |
3,3 |
1 |
0,630 |
0,026 |
0,087 |
0,286 |
Итог |
10,9 |
28 |
24,021 |
1,000 |
1,016 |
2,126 |
V= |
1,093 |
|
|
|
|
|
ОТВЕТ: Общие показатели:
-
номин доход
2,00
NPV
-1,59
D
1,02
G
2,57
V
-0,55