
Задача 2 ( Хренникова ( Васильева ) У05-721)
Дано:
М0=3000000
R1=10%
m 1= 1
T=1
R2=18,5
m 2=4
Вопрос:
Что выгоднее?
Решение:
М1=М0*(1+R1)=3300000
M2=M0*(1+R2/4)4=3594705
M1<M2
Ответ:
Выгоднее при начислении процентов каждый квартал
Задача 3(павлова
Дано:
М14=7989
М37=14329
m=4
найти:
R
M0
Решение:
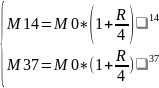
M37/M14=M0(1+R/4)37/M0(1+R/4)14=14329/7989
1,79359=(1+R/4)23
R=0,1028
M0=5600,2635
Задача №4. (Хусаинова Даша)
Определить: Что выгоднее: r1 = 19,8% при начислении процентов раз в месяц или r2 = 20,8% при начислении раз в квартал?
Решение:
Пусть М0 = 1000, тогда
M1 = M0*(1+r1/m1)12 = 1000*(1+0,198/12)12 = 1217
М2 = М0*(1+ r2/m2)4 = 1000*(1+0,208/4)4 = 1224,8
Ответ: выгоднее начисление процентов каждый квартал под r2 = 20,8%.
Задача 5 (Хренникова(Васильева) У05-721)
Дано:
M18=7929
M=12
R=14,2%
Найти:
M7
M0
M47
Решение:
M18=M0*(1+R/m)18
M0=M18/(1+R/m)18=6419,72
M47=M0*(1+R/m)47=11142,07
M7=M0*(1+R/m)7=6969,13
Задача 6 (Пушкарь Н.А. У05-721)
Дано :
МО=10 млн , Т=12 лет
Т1=5 лет R1=12% m1=4
T2=7 лет R2=10% m2=12
Найти M17 , M30 , M42 Решение :
n1 =m * t = 20 , n2= 84
M(T1)=M0*
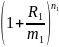
M(T2)=M(T1)*
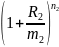
M17=M0*
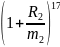 =
10*
=
10*
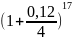 = 16.528 млн
= 16.528 млнM30= M0*
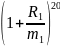 *
*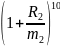 =
10*
=
10*
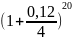 *
*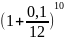 = 19,623
= 19,623
M42= M0* *
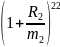 =
10*
*
=
10*
*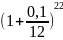 = 21,167
= 21,167
Задача 7 (Астраханцева Александра У05-721Б)
Дано:
Кладем деньги в банк на срок T=T1+T2=17 лет. Первые Т1=5 лет выплаты производятся ежеквартально m1=4 под ставку R1=12%, следующие Т2=12 лет выплаты производились ежемесячно m2=12. 38 выплаты М38=4937 и 51 выплата М51=6302.
Найти:
Необходимо найти ставку R2, М98, М(5), М(17)

М(0) М(5) М38 М51 М98 М(17)
Решение:
Найдем ставку R2.
Нам известны 38 и 51 выплаты второго периода.
Запишем уравнение:
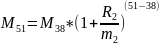
Выразим из уравнения R2
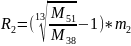
Подставим данные
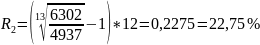
Найдем М(5).
За первый период было сделано T1*m1=20 выплат и последняя выплата первого периода является М(0) для второго , то есть М20 = М’(0). Запишем уравнение:
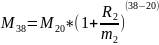
Выразим М20:

Подставим данные:
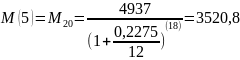
Найдем М98.
Выплата произошла во втором периоде. Составим уравнение:
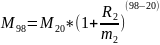
Подставим данные:
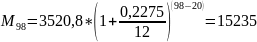
Найдем сколько мы получим по окончанию всего периода М(17).
За второй период было совершено Т2*m2=144 выплаты. Составим уравнение
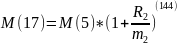
Подставим значения:
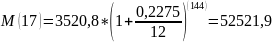
ОТВЕТ: R2=22,75%; M(5)=3520,8; M98=15235; M(17)=52521,9
Задача №8. (Хусаинова Даша)
Дано:
М48 = 9820
М0 = 6000
m = 4
Найти: r - ?
Решение:
М48 = М0*(1+r/m)48
M48/M0 = (1+r/m)48
1+r/m = (M48/M0)1/48
r = ((M48/M0)1/48 – 1)*m
r = ((9820/6000)1/48 -1)*4 = 0,0413 = 4,13%
Ответ: r = 4,13%.
Задача 9 (Астраханцева Александра У05-721Б)
Дано:
Кладем деньги в банк на срок T=T1+T2=29 лет. Первые Т1=8 лет выплаты производятся ежемесячно m1=12 под ставку R1=?%, следующие Т2=21 года выплаты производились ежеквартально m2=4 . 99 выплаты М99=7390 и 111 выплата М51=8211.
Найти:
Необходимо найти ставки R1, R2
М(0) М(8) М99 М111 М(29)
Решение:
Найдем ставку r2.
Нам известны 99 и 111 выплаты второго периода.
Запишем уравнение:
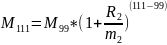
Выразим из уравнения R2
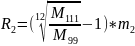
Подставим данные
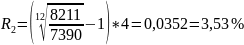
Найдем М(8).
За первый период было сделано T1*m1=96 выплат и последняя выплата первого периода является М(0) для второго , то есть М96 = М’(0). Запишем уравнение:
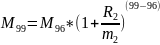
Выразим М20:
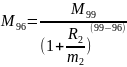
Подставим данные:
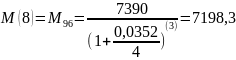
Так как для нахождения ставки R1 у нас недостаточно исходных данных, мы можем выразить R1 из уравнения через М0 :
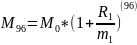
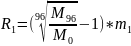
Подставим данные
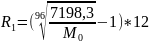
ОТВЕТ:
;
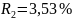
Задача 10 (Астраханцева Александра У05-721Б)
Дано:
Мы хотим заработать:
взять сумму М0 в кредит на условиях:
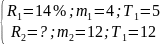
положить сумму М0 в банк на условиях:
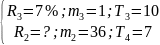
Найти:
Выяснить при каком соотношении неизвестных ставок мы получим доход. Составить график
Решение:
В момент времени Т0:
Берем кредит в банке М0
Кладем в банк М0
В момент времени Т:
Забираем сумму FVвкл
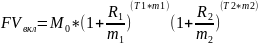
Отдаем долг FVзаем
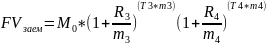
Составим уравнение и выразим из него R2
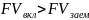
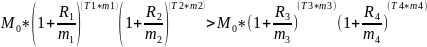
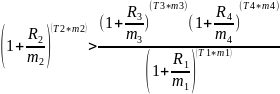
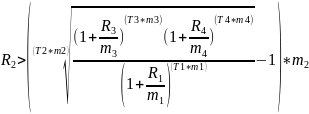
Подставим значения
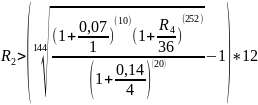
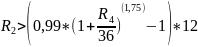
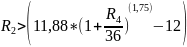
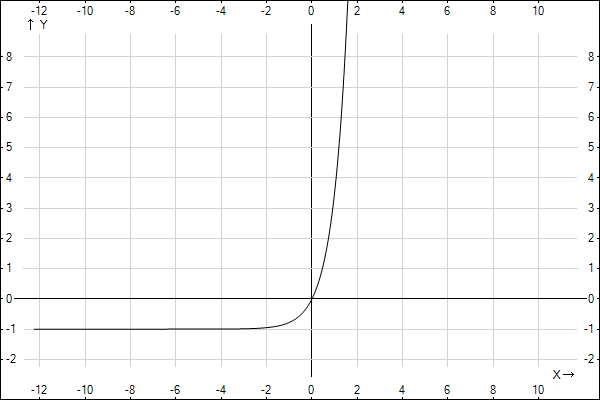
Построим график зависимости:
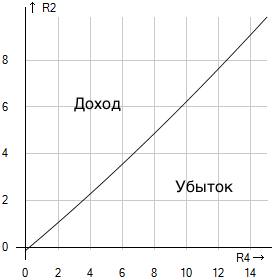
ОТВЕТ: зависимость ставок, при которых мы получим доход, описывается выражением
Задача №11. (Хусаинова Даша)
Дано:
Т2 = 7 лет
Т1 = 5 лет

ρ1 = 7%
R2 = 14%
m2 = 12
Найти:
Reff - ?
ρ3 - ?
Решение:
Пусть есть М0 – денег, тогда
М(Т1) = М0*еρ1*Т2
М(Т2) = М(Т1)*(1+R2/m2)84
М(Т1) = М0*е0,07*5 = 1,419*М0
М(Т2) = 1,419*М0*(1+0,14/12)84 = 3,7595*М0
Найдем reff и ρ3.
М(Т2) = М0*(1+reff)17
3,7595*М0 = М0*(1+reff)17
1+reff = (3,7595)1/17 = 1,081
Reff = 0,081 = 8,1%
ρ3 = ln(1+reff) = ln(1,081) = 0,0778 = 7,78%
Ответ: reff = 8,1%; ρ3 = 7,78%.
Задача №12. (Хусаинова Даша)
Дано:
Т2 = 7 лет
Т1 = 6 лет
М0 = 10 млн
М(Т2) = 60 млн
R1 = 21%
m1 = 4
Найти:
reff2 - ? ρ2 - ?
Решение:
Найдем М(Т1)
М(Т1) = М0*(1+R1/m1)24 = 10*(1+0,21/4)24 = 34,145
Найдем reff
reff2 = (M(T2)/M(T1))1/T2 – 1 = (60/10)1/7 – 1 = 0,0838 = 8,38%
Найдем ρ2
ρ2 = ln(1+reff2) = ln(1+0,0838) = 0,0804 = 8,04%
Ответ: reff = 8,38%, ρ2 = 8,04%.
№13 (%-е ставки: простая, эффективная, непрерывно начисляемая)
Туркина Маша У5-721
Дано:
Займ
T₁=7
m₁=4
R₁=14%
T₂=6
ρ₂=12%
T₃=8
reff₃=?
Вклад
T₄=12
ρ₄=?
T₅=11
m₅=12
R₅=14%
Построить график зависимости ρ₄ и reff₃.
Решение:
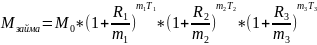
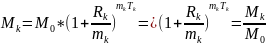
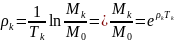
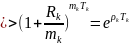
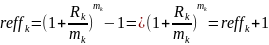
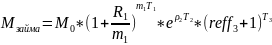
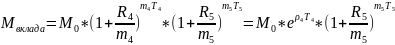
Условие
выгодности:
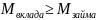
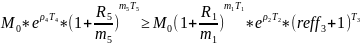
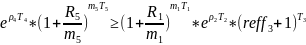
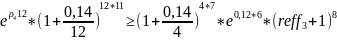
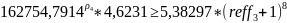
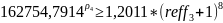
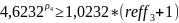
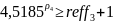
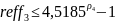
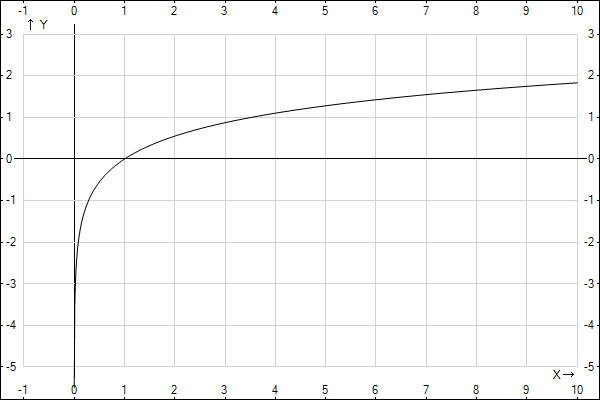
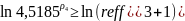
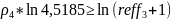
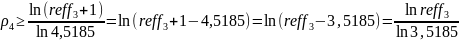
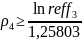
№14 (вексель)Туркина
Дано:
N=12 млн
ρ=8% - кредит
T=6
d=?
N₀=?
Решение:
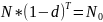
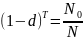
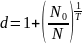
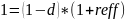
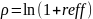
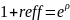
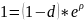
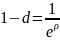
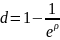
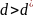
Пусть d=8,5%, тогда:
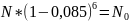
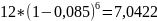 – цена векселя
– цена векселя
Сколько надо отдать в банк:
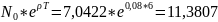
Доход:
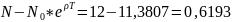
Задача №15. (Хусаинова Даша)
Дано:
Имеется в наличии вексель N1 = 10млн на срок Т1 = 5 лет. Мы планируем приобрести вексель N2 = 40 млн на срок Т2 = 2 года под d2 = 15%, ρзаим = 7%.
Найти: d1 - ?
Решение:
Вариант А:
Продаем вексель N1 по цене N1(T2)
N1(0) = N1*(1-d1)T2
Берем кредит для покупки векселя N2
M0 = N2(0) – N1(0)
Покупаем вексель N2 по цене N2(0)
N2(0) = N2*(1-d2)T2 = 40*(1-0,15)2 = 28,9 млн
Гасим вексель N2 в момент времени Т2
Возвращаем кредит М0 банку
М0 * еρзаим*T2
Доход А: N2-(N2(0)-N1(0))*eρзаим*Т2
Вариант В:
Ничего не делаем, гасим вексель N1 в момент времени Т1
Доход В: N1
Доход А>Дохода В, то есть
N2 - (N2(0)-N1(0))*eρзаим*Т2 > N1
N2 - N1 > (N2(0)-N1(0))*eρзаим*Т2
(N2 - N1)/eρзаим*Т2 > N2(0)-N1(0)
N1(0) > N2(0) – (N2-N1)/eρзаим*Т2
N1(0) > 28,9 – (40-10)/e0,07*2
N1(0) > 2,8192
N1(0) = N1*(1-d1)T1
d1 = 1 - (N1(0)/N1)1/T1
d1 = 1 – (2,8192/10)1/5
d1 = 0,2237 = 22,37%
Ответ: d1 = 22,37%
