16. Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость.

Если известны прямоугольные декартовы координаты направляющего вектора прямой и нормального вектора плоскости a = (a₁; a₂; a₃) и n = (А; В; С), то угол φ может быть вычислен с помощью формулы

или

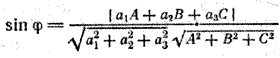        (1)

18. Определение расстояния между точкой и плоскостью.

Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость.

Поэтому решение этой задачи состоит из последовательного выполнения следующих графических операций:

1) из точки А опускаем перпендикуляра на плоскость а (рис.269);

2) находим точку М пересечения этого перпендикуляра с плоскостью М «= а П а;

3) определяем длину отрезка

• составляем уравнение прямой a, которая проходит через точку М₁ и перпендикулярна к плоскости  ;

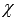• находим координаты 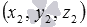  точки H₁ - точки пересечения прямой a и плоскости  ;

• вычисляем расстояние от точки М₁ до плоскости   по формуле 

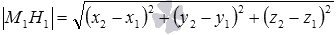
19. Пусть центр сферы находится в точке A (a; b; c), а радиус сферы равен R. Точками сферы являются те и только те точки пространства, расстояние от которых до точкиA равно R. Квадрат расстояния от любой точки B (x; y; z) сферы до точки A равен

(x – a)² + (y – b)² + (z – c)².

Поэтому уравнение сферы с центром A (a; b; c) и радиусом R имеет вид:

(x – a)² + (y – b)² + (z – c)² = R².